Презентация на тему: Методы построения сечений многогранников

Построение сечений многогранников Стереометрия 10 класс Выполнила учитель математики высшей категории МБОУ Кулешовской СОШ № 16 Коваль Э.Р. 5klass.net

Цель урока: закрепление полученных знаний построения сечений многогранников, углубление, систематизация и развитие их в перспективе (изучить метод следов).

«Скажи мне – и я забуду. Покажи мне – и я запомню. Вовлеки меня – и я научусь.» Древняя китайская пословица

Многие художники, искажая законы перспективы, рисуют необычные картины. Кстати, эти рисунки очень популярны среди математиков. В сети Internet можно найти множество сайтов, где публикуются эти невозможные объекты. Популярные художники Морис Эшер, Оскар Реутерсвард, Жос де Мей и другие, удивляли своими картинами математиков. http://lib.world-mobile.net/culture/special/imp/imp-world-r.narod.ru/art/index.html http://www.im-possible.info/english/art/mey/mey2.html http://alone.sammit.kiev.ua/moremind/illusion/index.html Это интересно!

Жос де Мей "Такое может нарисовать только тот, кто делает дизайн, не зная перспективы..."

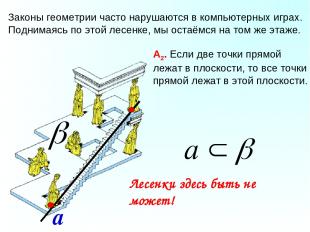
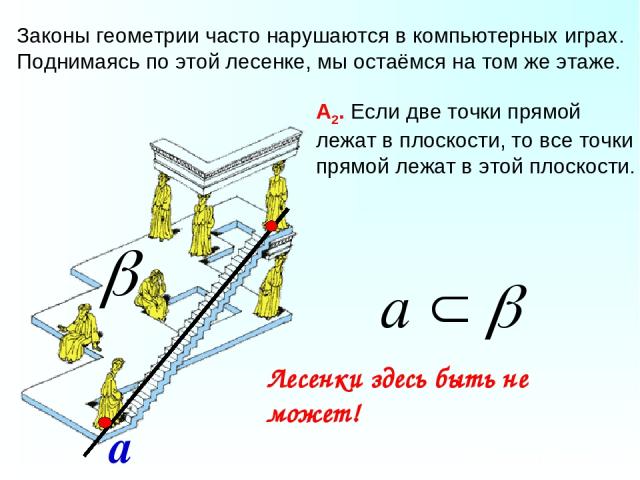
Законы геометрии часто нарушаются в компьютерных играх. Поднимаясь по этой лесенке, мы остаёмся на том же этаже. Лесенки здесь быть не может! а А2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.

"Те, кто влюбляются в практику без теории, уподобляются мореплавателю, садящемуся на корабль без руля и компаса и потому никогда не знающему, куда он плывет".          Леонардо да Винчи http://blogs.nnm.ru/page6/

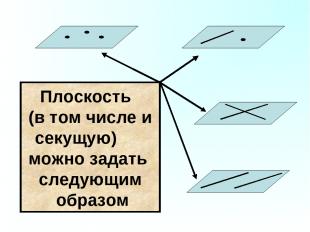
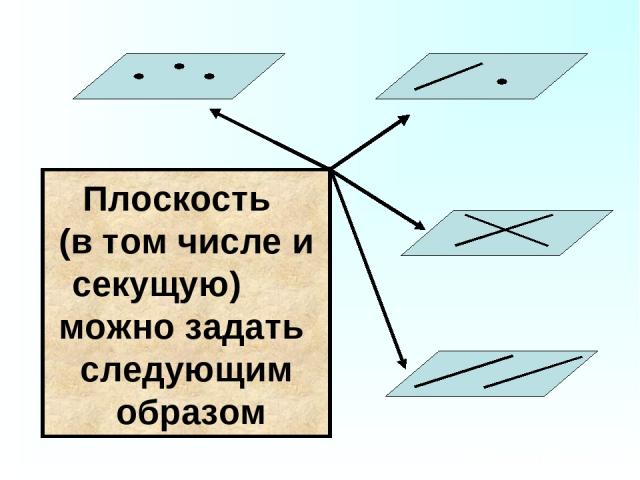
Плоскость (в том числе и секущую) можно задать следующим образом

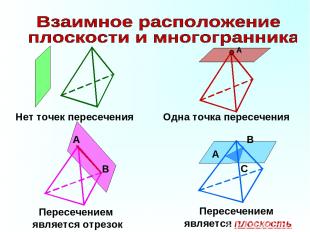
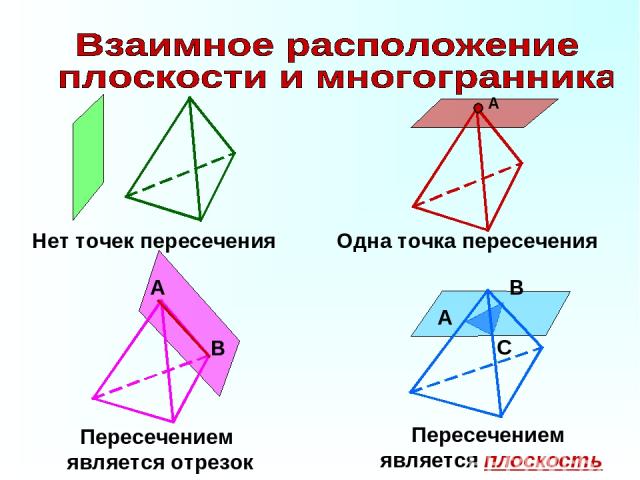
В А Нет точек пересечения Одна точка пересечения Пересечением является отрезок Пересечением является плоскость

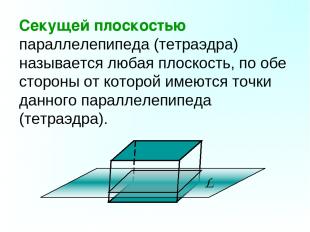
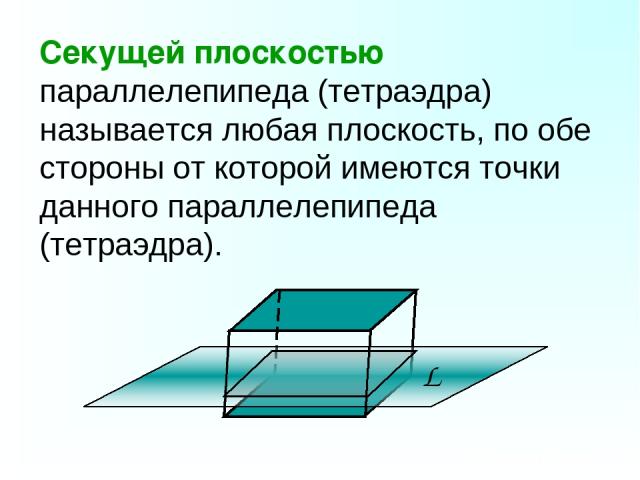
Секущей плоскостью параллелепипеда (тетраэдра) называется любая плоскость, по обе стороны от которой имеются точки данного параллелепипеда (тетраэдра).

Построить сечение многогранника плоскостью – это значит указать точки пересечения секущей плоскости с ребрами многогранника и соединить эти точки отрезками, принадлежащими граням многогранника. Для построения сечения многогранника плоскостью нужно в плоскости каждой грани указать 2 точки, принадлежащие сечению, соединить их прямой и найти точки пересечения этой прямой с ребрами многогранника.

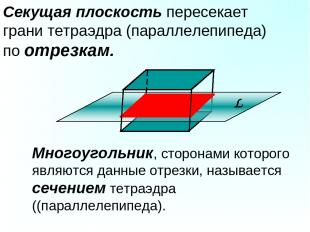
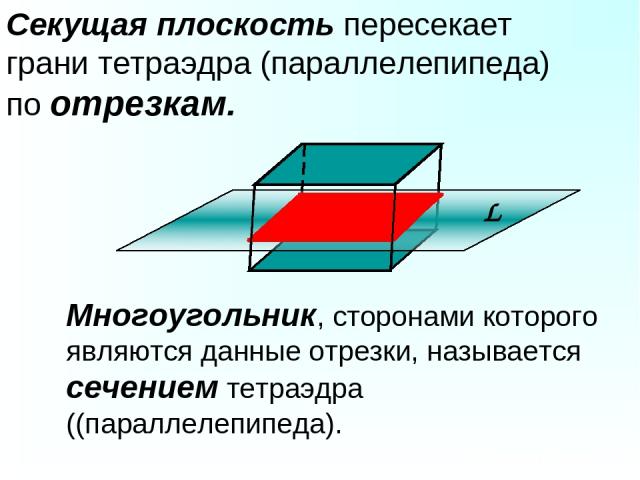
Секущая плоскость пересекает грани тетраэдра (параллелепипеда) по отрезкам. Многоугольник, сторонами которого являются данные отрезки, называется сечением тетраэдра ((параллелепипеда).

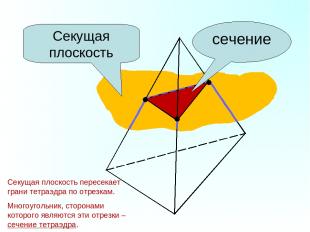
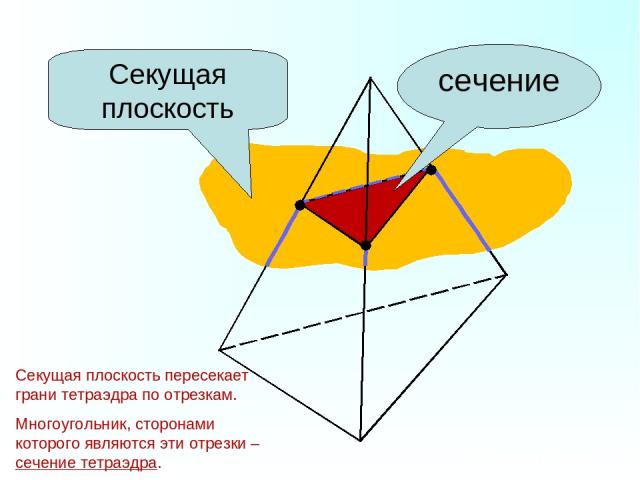
Секущая плоскость сечение Секущая плоскость пересекает грани тетраэдра по отрезкам. Многоугольник, сторонами которого являются эти отрезки – сечение тетраэдра.

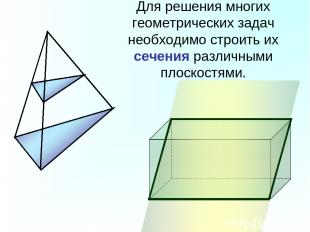
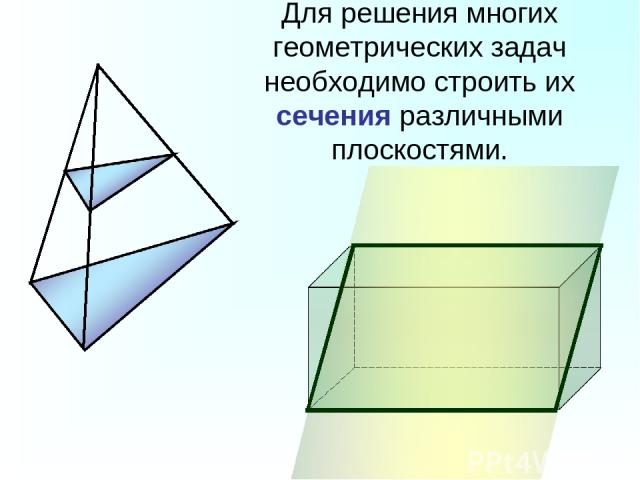
Для решения многих геометрических задач необходимо строить их сечения различными плоскостями.

АКСИОМЫ планиметрия стереометрия 1. Каждой прямой принадлежат по крайней мере две точки 2. Имеются по крайней мере три точки, не лежащие на одной прямой 3. Через любые две точки проходит прямая, и притом только одна. Характеризуют взаимное расположение точек и прямых Основное понятие геометрии «лежать между» 4. Из трех точек прямой одна и только одна лежит между двумя другими. А1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна А2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости А3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

При этом необходимо учитывать следующее: 1. Соединять можно только две точки, лежащие в плоскости одной грани. Для построения сечения нужно построить точки пересечения секущей плоскости с ребрами и соединить их отрезками. 2. Секущая плоскость пересекает параллельные грани по параллельным отрезкам. 3. Если в плоскости грани отмечена только одна точка, принадлежащая плоскости сечения, то надо построить дополнительную точку. Для этого необходимо найти точки пересечения уже построенных прямых с другими прямыми, лежащими в тех же гранях.

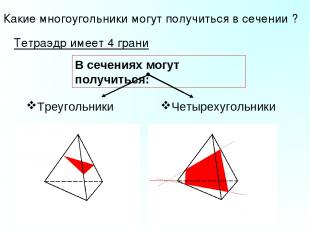
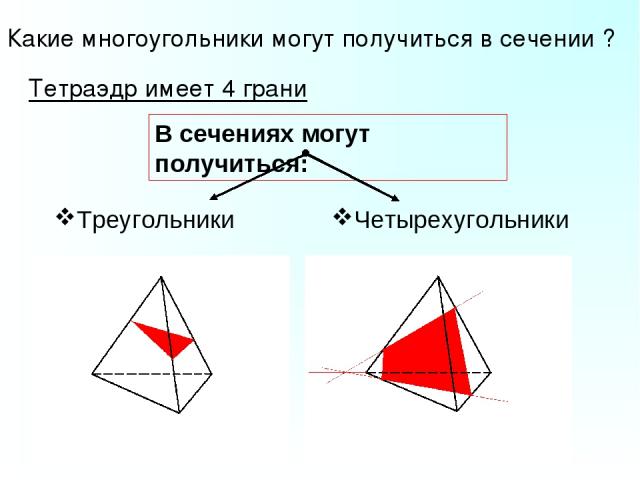
Какие многоугольники могут получиться в сечении ? Тетраэдр имеет 4 грани В сечениях могут получиться: Четырехугольники Треугольники

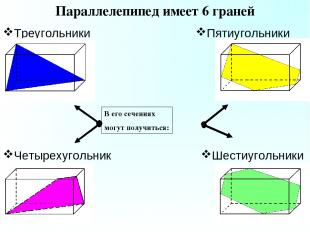
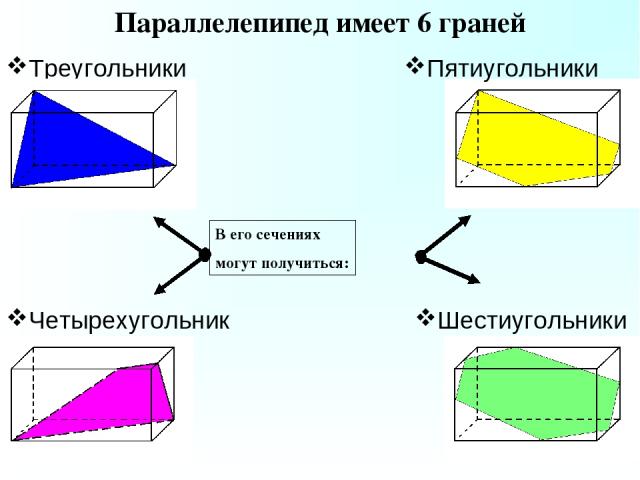
Треугольники Параллелепипед имеет 6 граней Четырехугольники Шестиугольники Пятиугольники В его сечениях могут получиться:

Блиц - опрос Задача блиц – опроса: ответить на вопросы и обосновать ответ с помощью аксиом, теорем и свойств параллельных плоскостей.

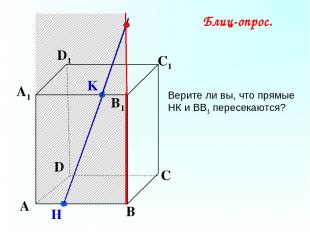
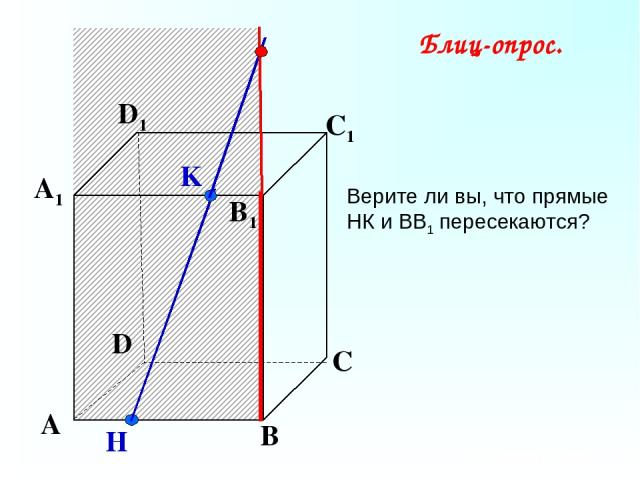
K А В С D А1 D1 С1 B1 H Блиц-опрос. Верите ли вы, что прямые НК и ВВ1 пересекаются?

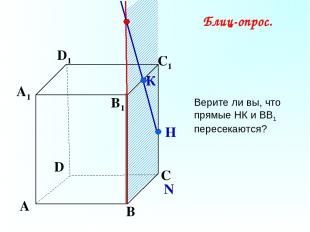
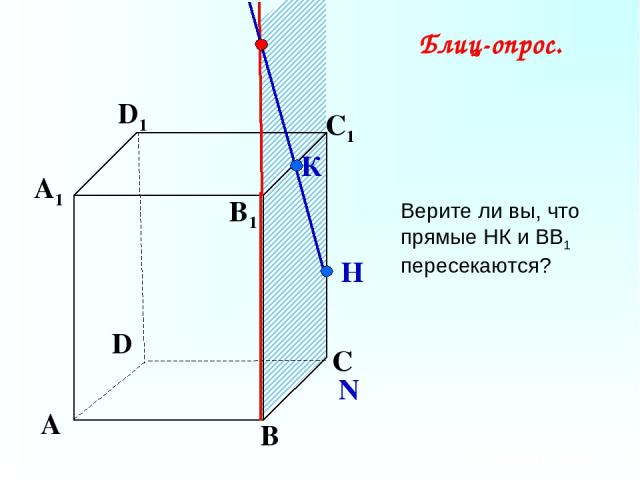
А В С D А1 D1 С1 B1 N К Н Блиц-опрос. Верите ли вы, что прямые НК и ВВ1 пересекаются?

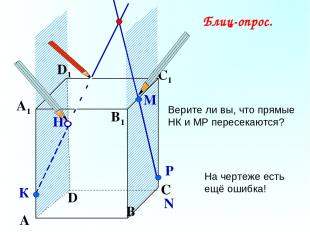
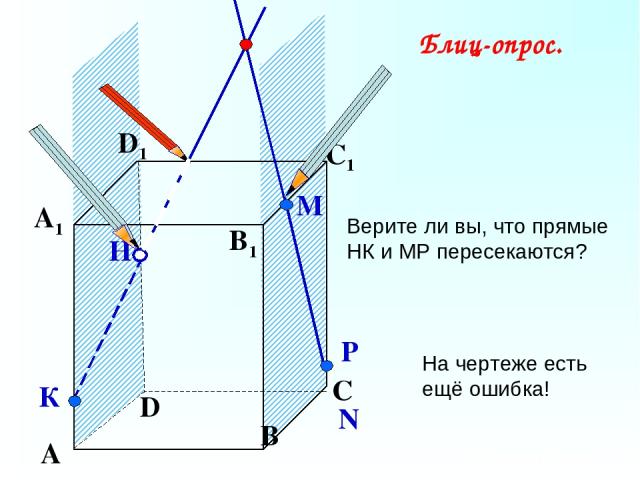
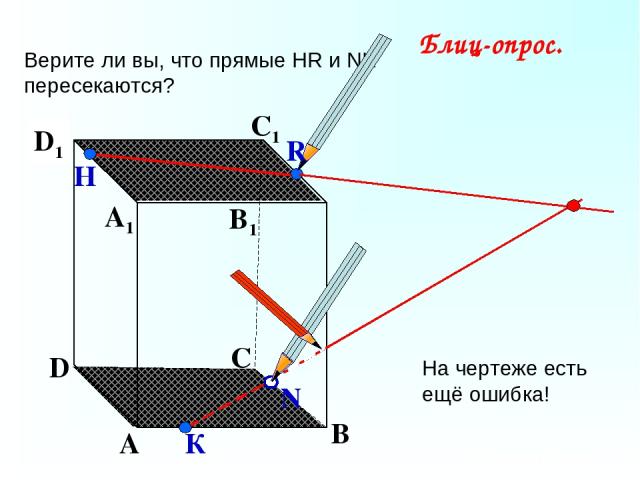
А В С D А1 D1 С1 B1 Верите ли вы, что прямые НК и МР пересекаются? N Р Н К М Блиц-опрос. На чертеже есть ещё ошибка!

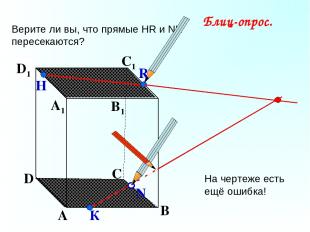
А В С D А1 D1 С1 B1 Верите ли вы, что прямые НR и NK пересекаются? N Н К Блиц-опрос. R На чертеже есть ещё ошибка!

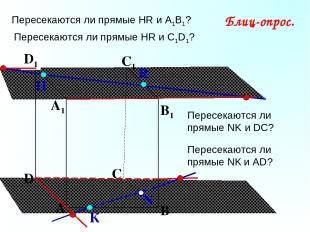
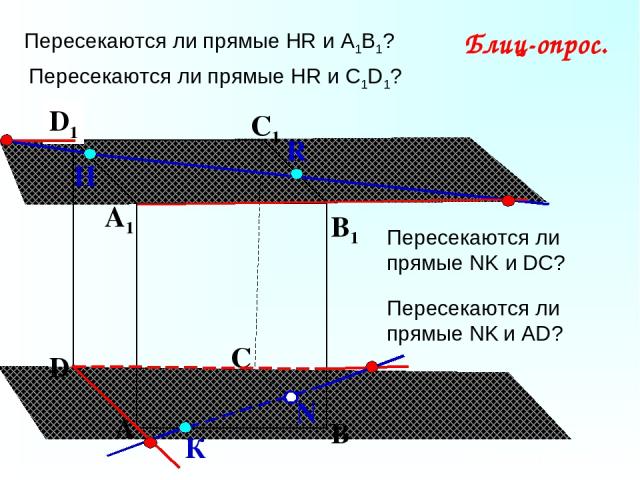
А В С D А1 D1 С1 B1 Пересекаются ли прямые НR и А1В1? N Н К Блиц-опрос. R Пересекаются ли прямые НR и С1D1? Пересекаются ли прямые NK и DC? Пересекаются ли прямые NK и АD?

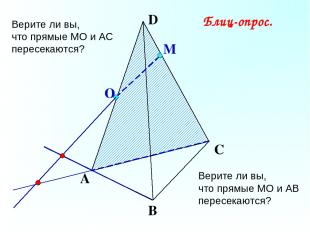
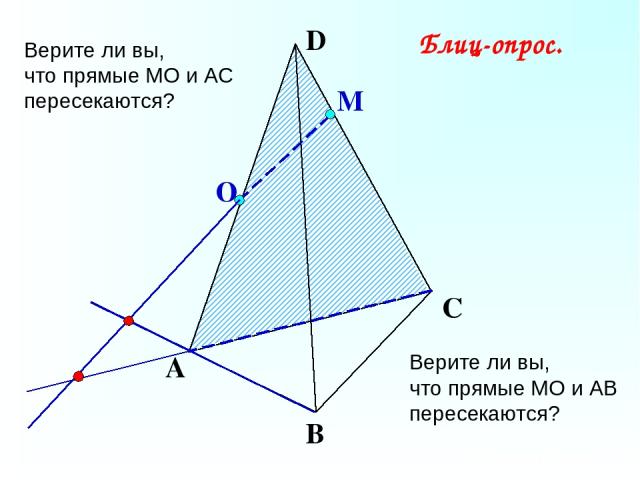
О М А В С D Верите ли вы, что прямые МО и АС пересекаются? Блиц-опрос. Верите ли вы, что прямые МО и АВ пересекаются?

Умение решать задачи – практическое искусство, подобное плаванию, или катанию на лыжах … : научиться этому можно лишь подражая избранным образцам и постоянно тренируясь.. Д. Пойа

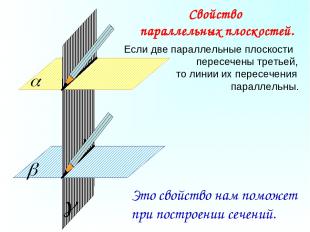
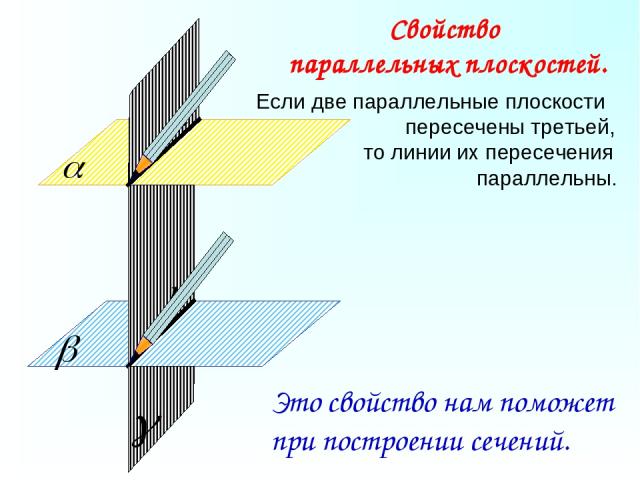
Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. Свойство параллельных плоскостей. Это свойство нам поможет при построении сечений.

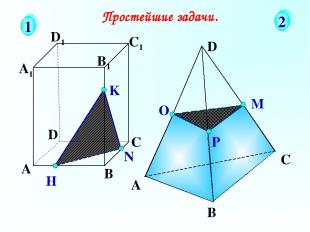
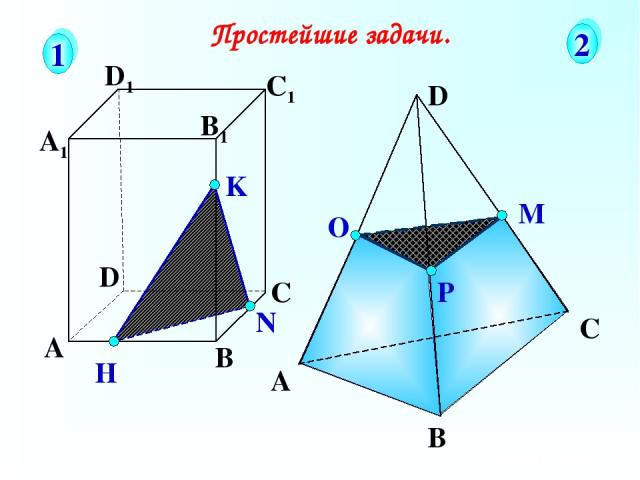
А В С D А1 D1 С1 B1 N H K Простейшие задачи. 1 2

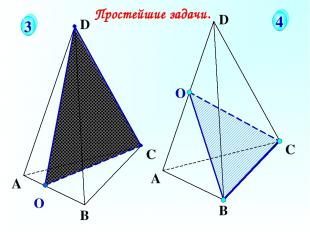
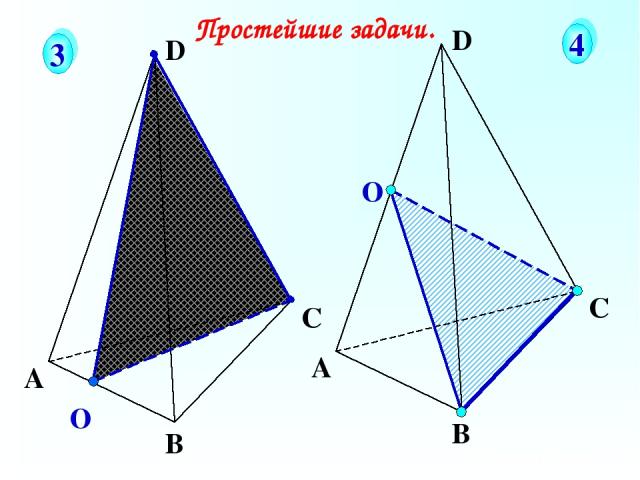
О А В С D Простейшие задачи. 3 4 О А В С D

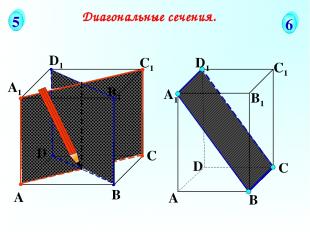
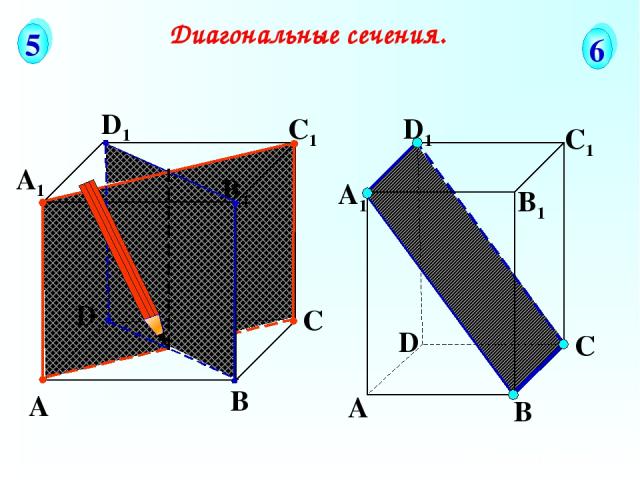
А В С D А1 D1 С1 B1 Диагональные сечения. 5 6

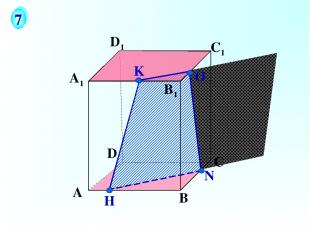
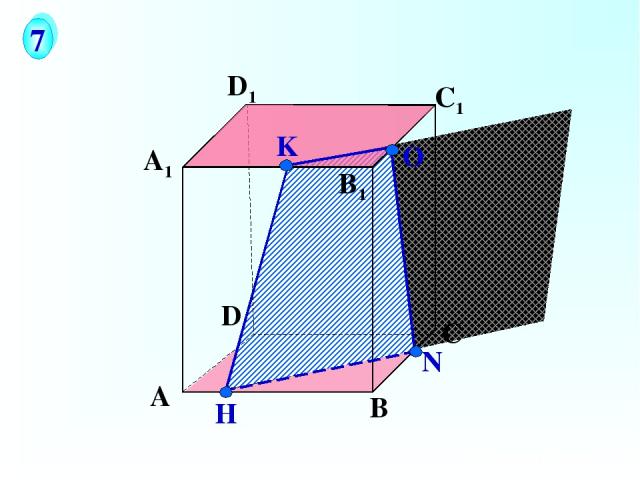
А В С D А1 D1 С1 B1 N H О 7 K

Аксиоматический метод Метод следов Суть метода заключается в построении вспомогательной прямой, являющейся изображением линии пересечения секущей плоскости с плоскостью какой-либо грани фигуры . Удобнее всего строить изображение линии пересечения секущей плоскости с плоскостью нижнего основания. Эту линию называют следом секущей плоскости. Используя след, легко построить изображения точек секущей плоскости, находящихся на боковых ребрах или гранях фигуры .    

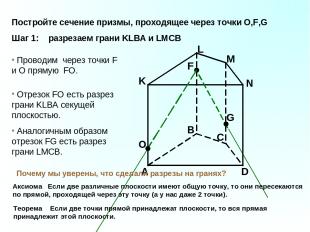
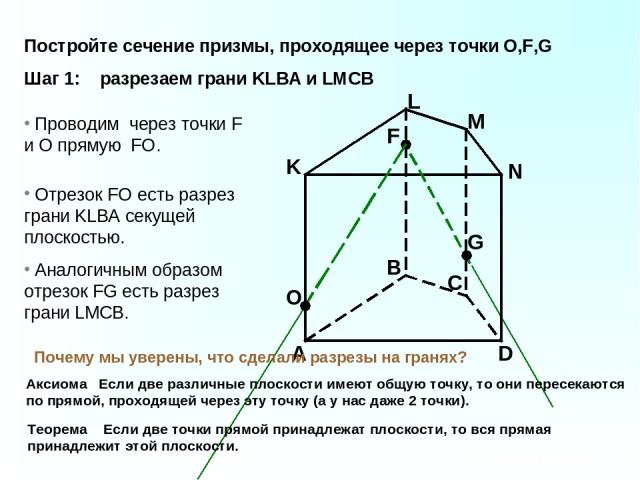
A B C D K L M N F G Проводим через точки F и O прямую FO. O Отрезок FO есть разрез грани KLBA секущей плоскостью. Аналогичным образом отрезок FG есть разрез грани LMCB. Аксиома Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку (а у нас даже 2 точки). Теорема Если две точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскости. Почему мы уверены, что сделали разрезы на гранях? Постройте сечение призмы, проходящее через точки O,F,G Шаг 1: разрезаем грани KLBA и LMCB

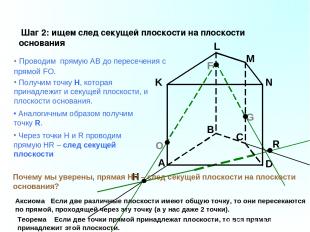
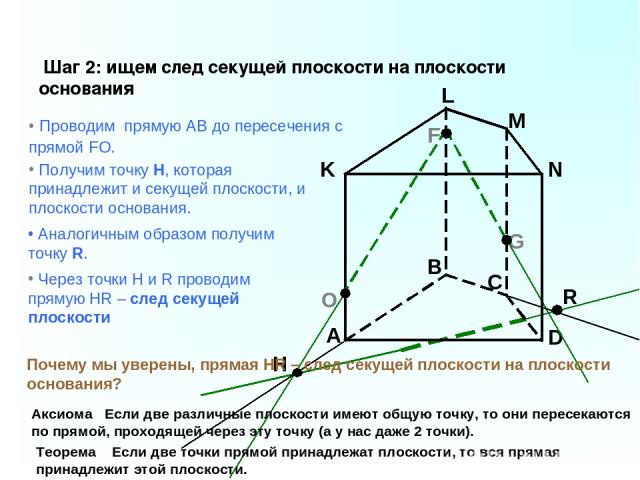
A B C D K L M N F G Шаг 2: ищем след секущей плоскости на плоскости основания Проводим прямую АВ до пересечения с прямой FO. O Получим точку H, которая принадлежит и секущей плоскости, и плоскости основания. Аналогичным образом получим точку R. Аксиома Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку (а у нас даже 2 точки). Теорема Если две точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскости. Через точки H и R проводим прямую HR – след секущей плоскости Почему мы уверены, прямая HR – след секущей плоскости на плоскости основания?

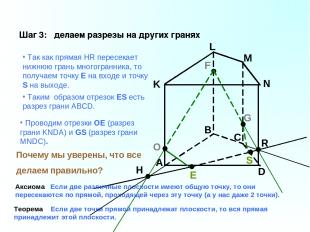
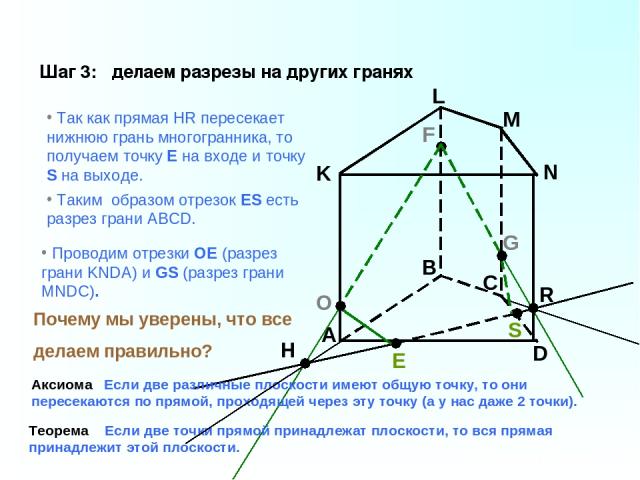
A B C D K L M N F G Шаг 3: делаем разрезы на других гранях Так как прямая HR пересекает нижнюю грань многогранника, то получаем точку E на входе и точку S на выходе. O Таким образом отрезок ES есть разрез грани ABCD. Аксиома Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку (а у нас даже 2 точки). Теорема Если две точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскости. Проводим отрезки ОЕ (разрез грани KNDA) и GS (разрез грани MNDC). Почему мы уверены, что все делаем правильно?

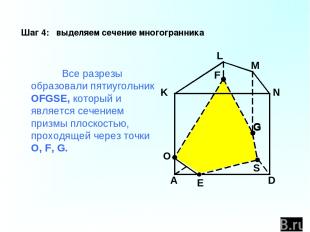
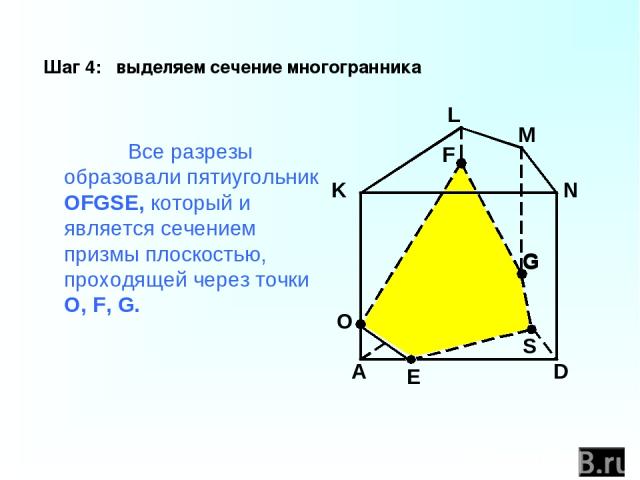
C B A D K L M N F G Шаг 4: выделяем сечение многогранника Все разрезы образовали пятиугольник OFGSE, который и является сечением призмы плоскостью, проходящей через точки O, F, G. O G

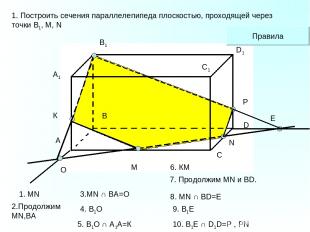
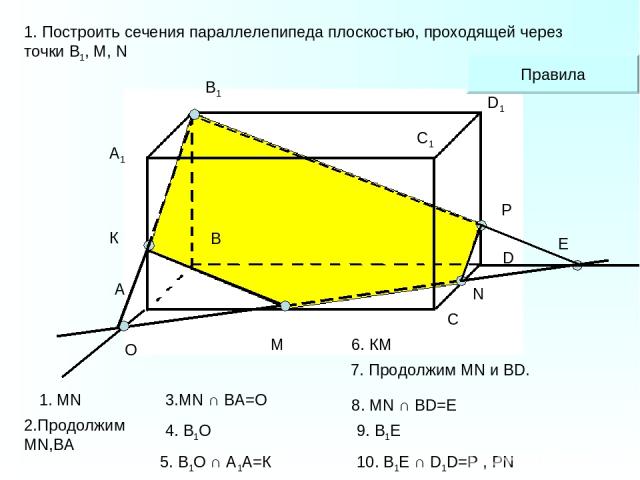
A1 А В В1 С С1 D D1 M N 1. Построить сечения параллелепипеда плоскостью, проходящей через точки В1, М, N O К Е P Правила 1. MN 2.Продолжим MN,ВА 4. В1О 6. КМ 7. Продолжим MN и BD. 9. В1E 5. В1О ∩ А1А=К 8. MN ∩ BD=E 10. B1Е ∩ D1D=P , PN 3.MN ∩ BA=O

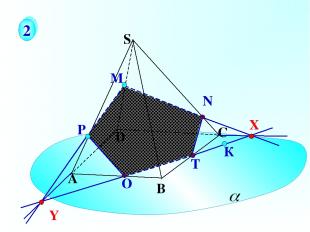
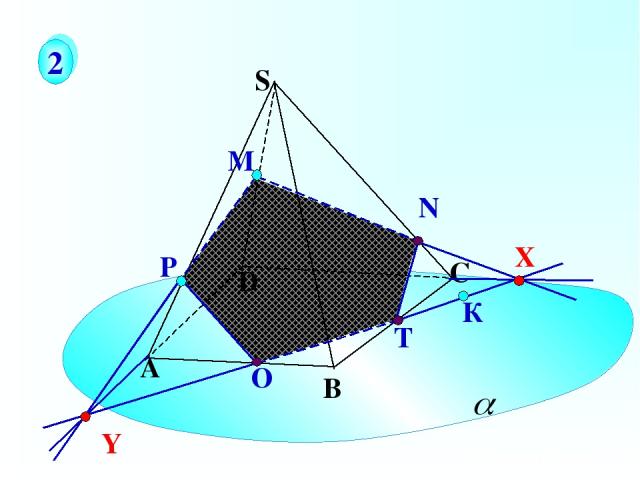
Р О Т А В С S D К М 2 X

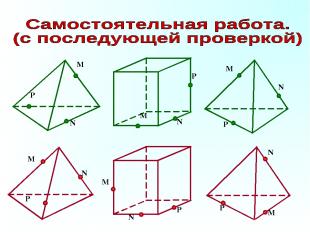
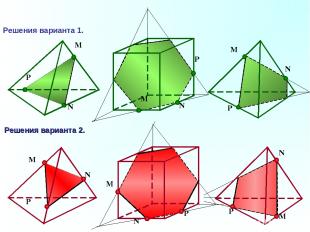
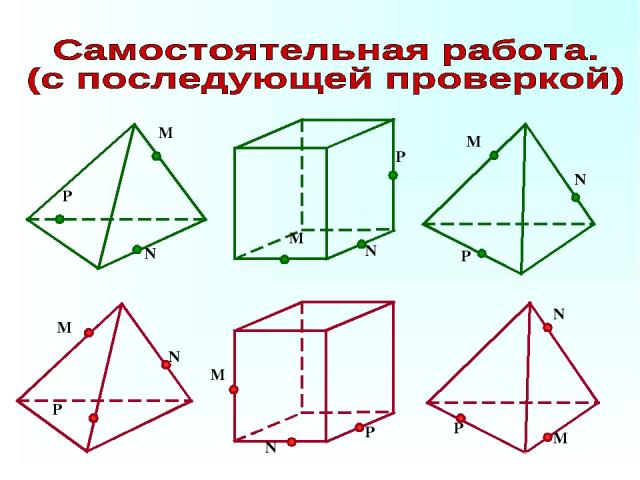
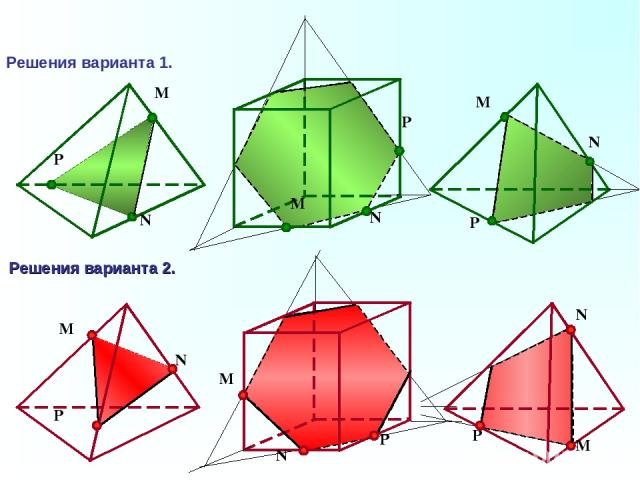
P N M N P M N P M Решения варианта 1. Решения варианта 2. M N P M N P M N P

Правила для самоконтроля: Вершины сечения находятся только на ребрах. Стороны сечения находятся только на грани многогранника. Секущая плоскость пересекает грань или плоскость грани, то только один раз.

Составить две задачи на построение сечений многогранников с использованием полученных знаний.

Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их (Д. Пойа)

* Атанасян Л.С., и др. Геометрия 10-11. – М.: Просвещение, 2008. Литвиненко В.Н., Многогранники. Задачи и решения. – М.: Вита-Пресс, 1995. Смирнов В.А., Смирнова И. М., ЕГЭ 100 баллов. Геометрия. Сечение многогранников. – М.: Экзамен, 2011. Учебно-методическое приложение к газете «Первое сентября» «Математика». Федотова О., Кабакова Т. Интегрированный урок "Построение сечений призмы", 9/2010. Зив Б.Г. Дидактические материалы по геометрии для 10 класса. – М., Просвещение, 1997. Электронное издание «1С: Школа. Математика, 5-11 кл. Практикум» 7. http://www.edu.yar.ru/russian/pedbank/sor_uch/math/legcosh/work.html