Презентация на тему: Касательная к графику функции

Касательная к графику функции Подготовила: ученица 11 класса «Д»Красовская ВикторияРуководители: Крагель Т.П., Гремяченская Т.В

Содержание: Появление понятия касательнойИстория появления касательнойПостроение касательнойПример построения касательной: 1 часть2 часть3 часть

Появление понятия касательной Понятие касательной – одно из древнейших в математике. В геометрии касательную к окружности определяют как прямую, имеющую ровно одну точку пересечения с этой окружностью. Древние с помощью циркуля и линейки умели проводить касательные к окружности, а в последствии – к коническим сечениям: эллипсам, гиперболам и параболам.

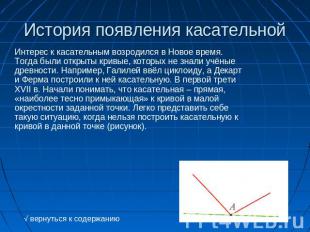
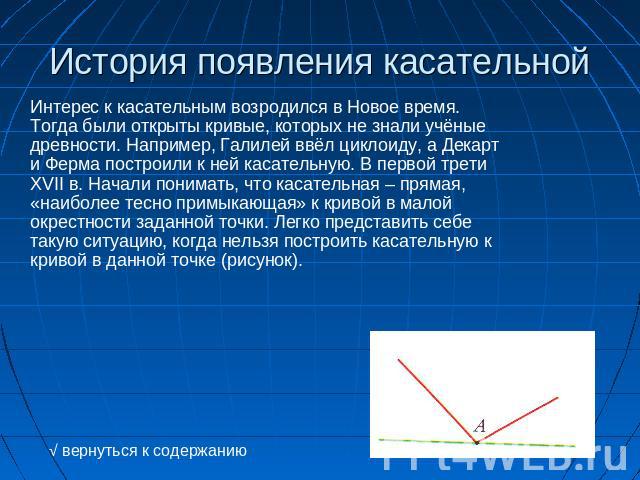
История появления касательной Интерес к касательным возродился в Новое время. Тогда были открыты кривые, которых не знали учёные древности. Например, Галилей ввёл циклоиду, а Декарт и Ферма построили к ней касательную. В первой трети XVII в. Начали понимать, что касательная – прямая, «наиболее тесно примыкающая» к кривой в малой окрестности заданной точки. Легко представить себе такую ситуацию, когда нельзя построить касательную к кривой в данной точке (рисунок).

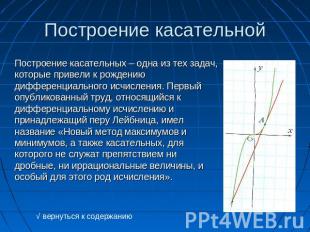
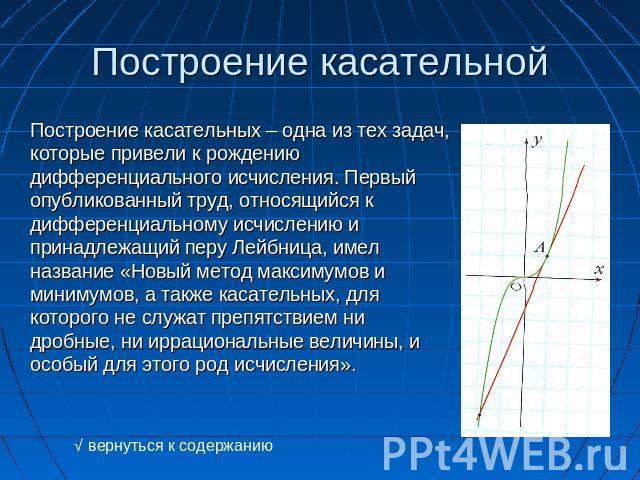
Построение касательной Построение касательных – одна из тех задач, которые привели к рождению дифференциального исчисления. Первый опубликованный труд, относящийся к дифференциальному исчислению и принадлежащий перу Лейбница, имел название «Новый метод максимумов и минимумов, а также касательных, для которого не служат препятствием ни дробные, ни иррациональные величины, и особый для этого род исчисления».

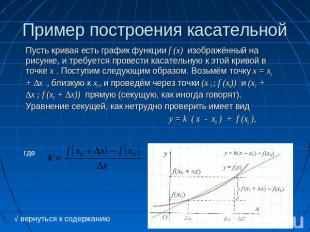
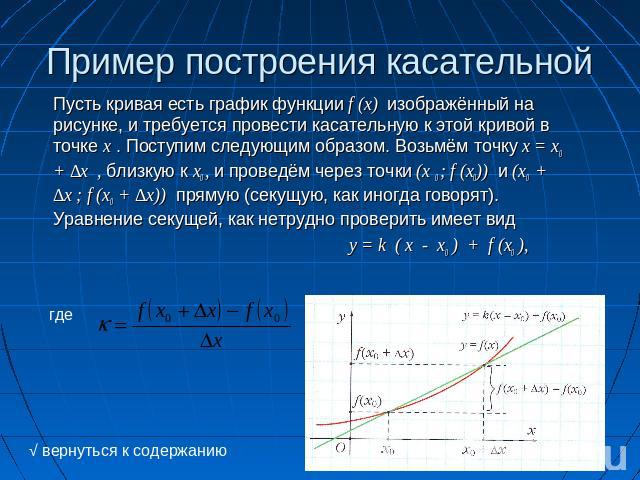
Пример построения касательной Пусть кривая есть график функции f (x) изображённый на рисунке, и требуется провести касательную к этой кривой в точке x . Поступим следующим образом. Возьмём точку x = x0 + ∆x , близкую к х0 , и проведём через точки (х 0 ; f (x0)) и (х0 + ∆х ; f (х0 + ∆х)) прямую (секущую, как иногда говорят). Уравнение секущей, как нетрудно проверить имеет видy = k ( x - x0 ) + f (x0 ), √ вернуться к содержанию

Если существует предел то прямую и называют касательной к графику функции f(x) в точке x0 . Если сказать иначе, касательную можно определить как прямую, которая является предельным положением секущих, когда ∆x стремится к 0.Из определения величины k0 видно, что функция Стремится к 0, когда ∆x стремится к 0. Последнее равенство означает, что √ вернуться к содержанию

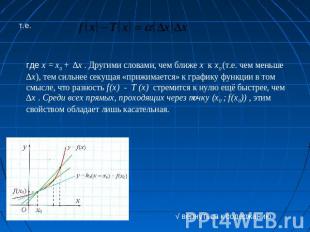
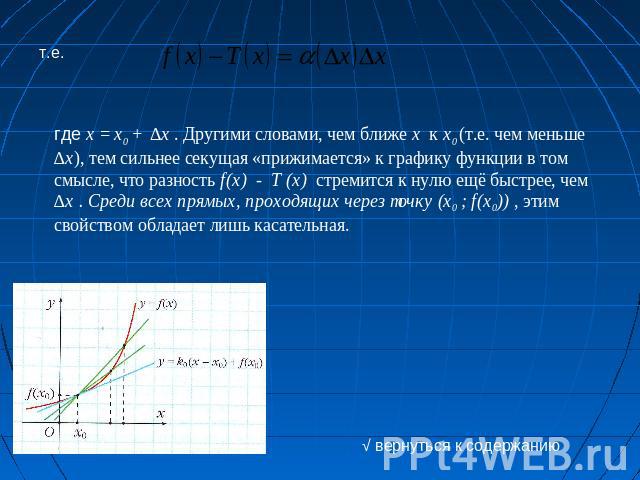
где x = x0 + ∆x . Другими словами, чем ближе x к x0 (т.е. чем меньше ∆x), тем сильнее секущая «прижимается» к графику функции в том смысле, что разность f(x) - T (x) стремится к нулю ещё быстрее, чем ∆x . Среди всех прямых, проходящих через точку (x0 ; f(x0)) , этим свойством обладает лишь касательная. √ вернуться к содержанию