Презентация на тему: Геометрические задачи в ЕГЭ

Геометрические задачи в ЕГЭ Презентация учителя МБОУ «Знаменская средняя общеобразовательная школа» Орловского района Орловской области Гильц С.И. № 247-832-315 Цель урока: обобщить, систематизировать и закрепить знания обучающихся по теме. 5klass.net

ЕГЭ Сегодня многие выпускники, 11- классники реально боятся сдавать ЕГЭ по математике. А если человек боится, то, как известно, чтобы запугать его еще сильнее, никаких особых усилий прилагать не нужно. Поэтому надо научиться решать минимум заданий. Программа минимум в этом случае – научиться решать задачи уровней B1, B2, B4, B5, B7 как самые что ни на есть простые. Геометрические задачи:простые-В3,В6,сложнее-В9,В11,сложные - С2, повышенной сложности - С4.

Уметь выполнять действия с геометрическими фигурами, координатами и векторами, а именно: 1.Решать планиметрические задачи на нахождение геометрических величин (длин, углов, площадей) 2. Решать простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объемов); использовать при решении стереометрических задач планиметрические факты и методы 3.Определять координаты точки; проводить операции над векторами, вычислять длину и координаты вектора, угол между векторами

Варианты задач: Задача1 Задача 2

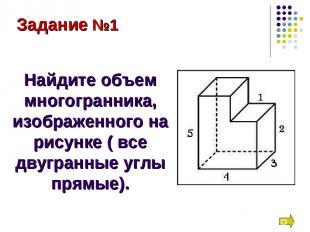
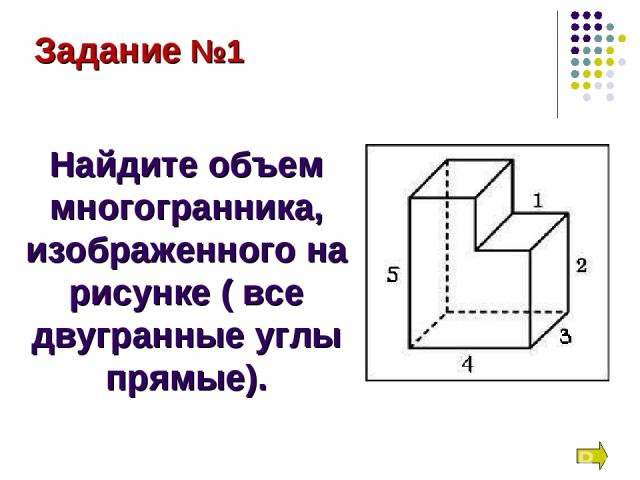
Задание №1 Найдите объем многогранника, изображенного на рисунке ( все двугранные углы прямые).

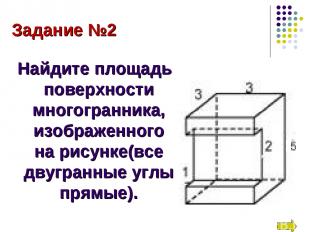
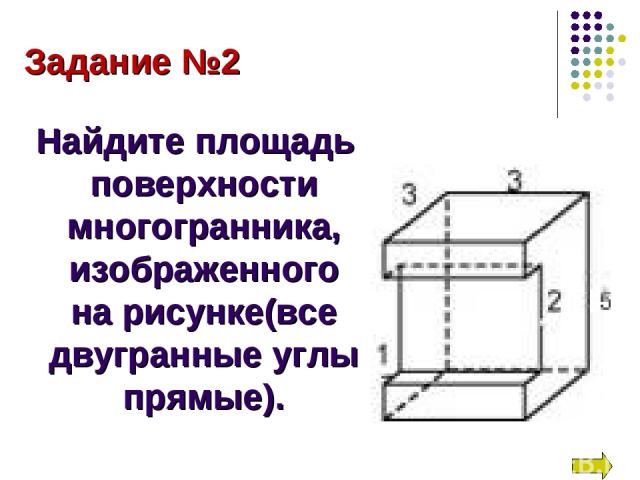
Задание №2 Найдите площадь поверхности многогранника, изображенного на рисунке(все двугранные углы прямые).

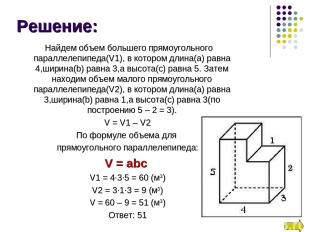
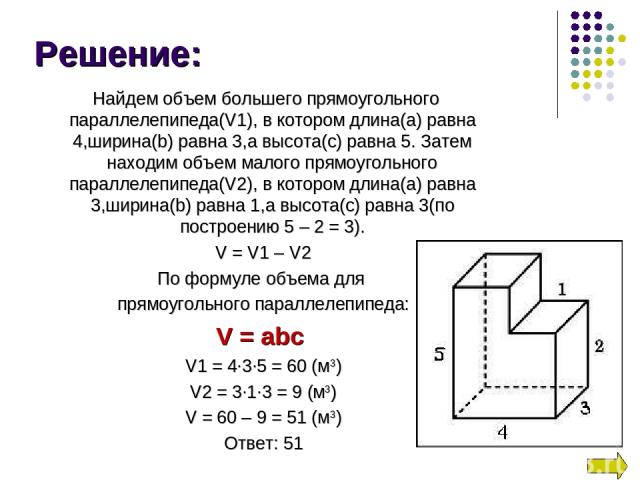
Найдем объем большего прямоугольного параллелепипеда(V1), в котором длина(а) равна 4,ширина(b) равна 3,а высота(с) равна 5. Затем находим объем малого прямоугольного параллелепипеда(V2), в котором длина(а) равна 3,ширина(b) равна 1,а высота(с) равна 3(по построению 5 – 2 = 3). V = V1 – V2 По формуле объема для прямоугольного параллелепипеда: V = abc V1 = 4∙3∙5 = 60 (м3) V2 = 3∙1∙3 = 9 (м3) V = 60 – 9 = 51 (м3) Ответ: 51 Решение:

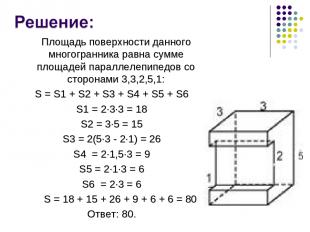
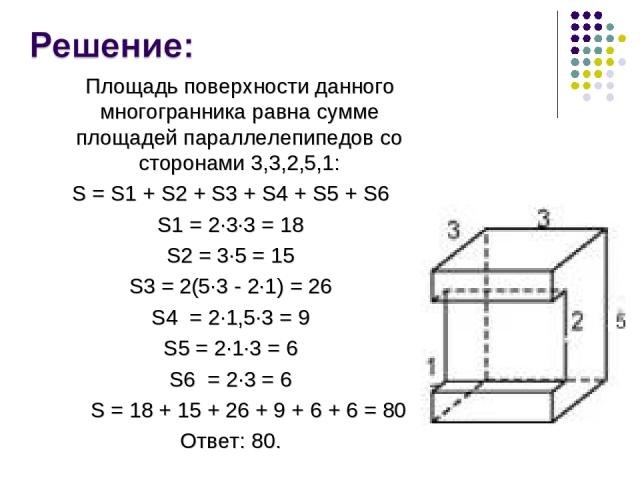
Площадь поверхности данного многогранника равна сумме площадей параллелепипедов со сторонами 3,3,2,5,1: S = S1 + S2 + S3 + S4 + S5 + S6 S1 = 2∙3∙3 = 18 S2 = 3∙5 = 15 S3 = 2(5∙3 - 2∙1) = 26 S4 = 2∙1,5∙3 = 9 S5 = 2∙1∙3 = 6 S6 = 2∙3 = 6 S = 18 + 15 + 26 + 9 + 6 + 6 = 80 Ответ: 80.

Устные упражнения

Что собой представляют задания части В3? Задание В3 является геометрической задачей. Задача настолько может быть легкой, что с ней может справиться и второклассник, впервые познакомившийся с понятием “площадь”. 

Для успешного решения задач типа В3 необходимо: Уметь выполнять действия с геометрическими фигурами, координатами векторов. Решать планиметрические задачи на нахождение геометрических величин (длин, углов, площадей). Моделировать реальные ситуации на языке геометрии, исследовать  построенные модели с использованием геометрических понятий и  теорем, аппарата алгебры; решать практические задачи, связанные с  нахождением геометрических величин.

Для успешного решения задач типа В3 необходимо: Повторить материал по темам: Планиметрия. Треугольник. Параллелограмм, прямоугольник, ромб, квадрат. Трапеция. Окружность и круг. Площадь треугольника, параллелограмма, трапеции, круга, сектора.

Возможные задания: Задание №1 Задание №2 Задание №3 Задание №4 Задание №5 Задание №6

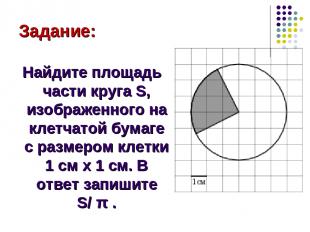
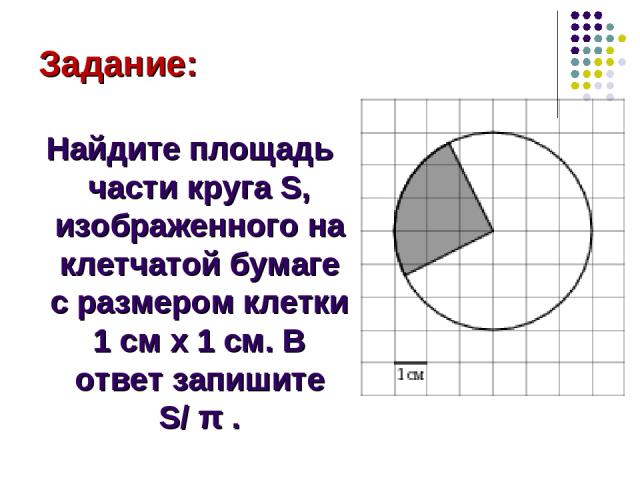
Задание: Найдите площадь части круга S, изображенного на клетчатой бумаге с размером клетки 1 см x 1 см. В ответ запишите S/ π .

Решение: Площадь круга находиться по формуле: S = πR², где R - радиус. В нашем случае  R = 3 см. Однако на рисунке заштрихован не весь круг, а лишь его четвертинка (т.к. угол между двумя радиусами, которые ограничивают заштрихованную часть составляет 90º)    Тогда площадь заштрихованной части S = 0,25π ∙ 3² = 2,25 π (см²) Ответ: 2,25 

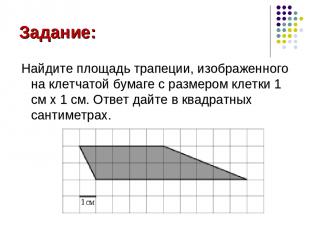
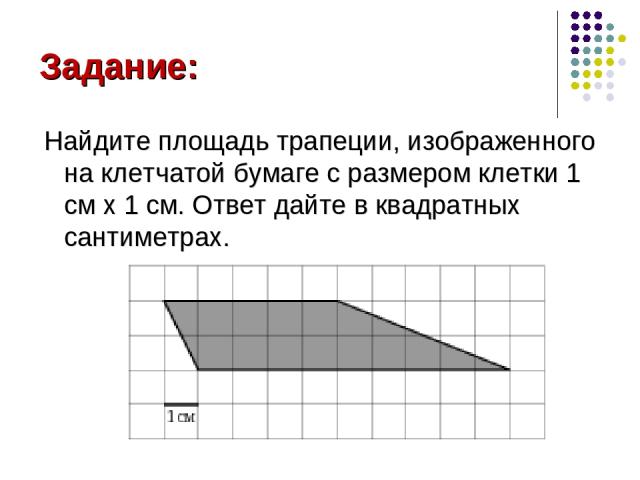
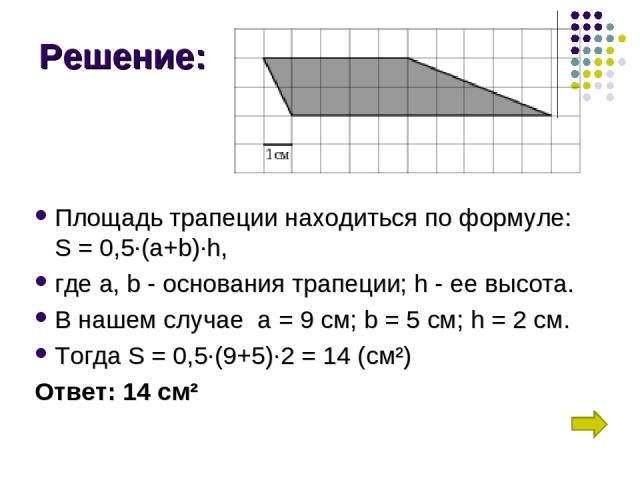
Задание: Найдите площадь трапеции, изображенного на клетчатой бумаге с размером клетки 1 см x 1 см. Ответ дайте в квадратных сантиметрах.

Решение: Площадь трапеции находиться по формуле: S = 0,5∙(a+b)∙h, где а, b - основания трапеции; h - ее высота. В нашем случае  а = 9 см; b = 5 см; h = 2 см. Тогда S = 0,5∙(9+5)∙2 = 14 (см²) Ответ: 14 см²

Задание: Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см x 1 см. Ответ дайте в квадратных сантиметрах.

Решение: Площадь треугольника находиться по формуле: S = 0,5∙a∙h, где а - основание треугольника; h - его высота. В нашем случае  а = 6 см;  h = 5 см. Тогда S = 0,5 ∙ 6 ∙ 5 = 15 (см²) Ответ: 15 см²

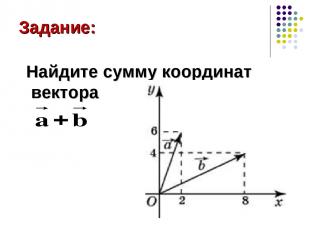
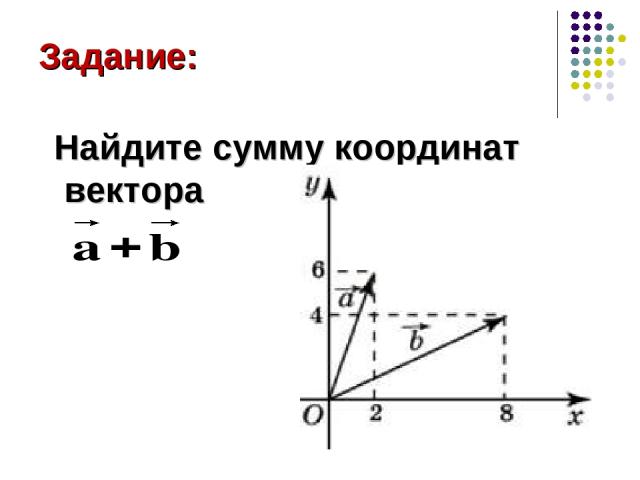
Задание: Найдите сумму координат вектора

Решение:

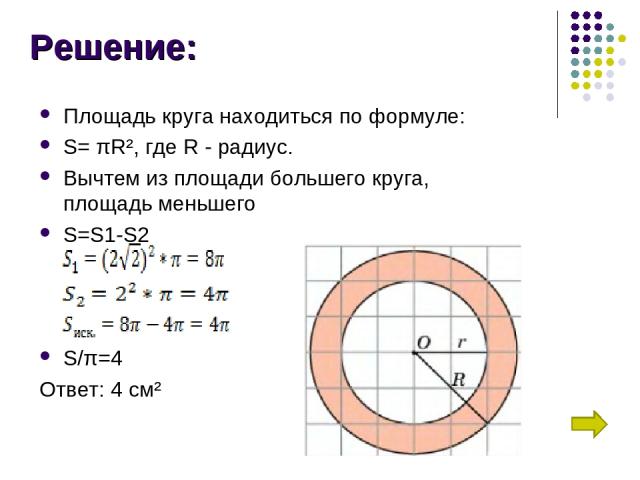
Задание: Найдите площадь S кольца, считая стороны квадратных клеток равными 1. В ответе укажите S/π.

Решение: Площадь круга находиться по формуле: S= πR², где R - радиус. Вычтем из площади большего круга, площадь меньшего S=S1-S2 S/π=4 Ответ: 4 см²

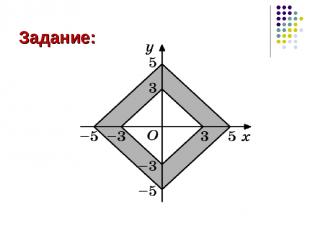
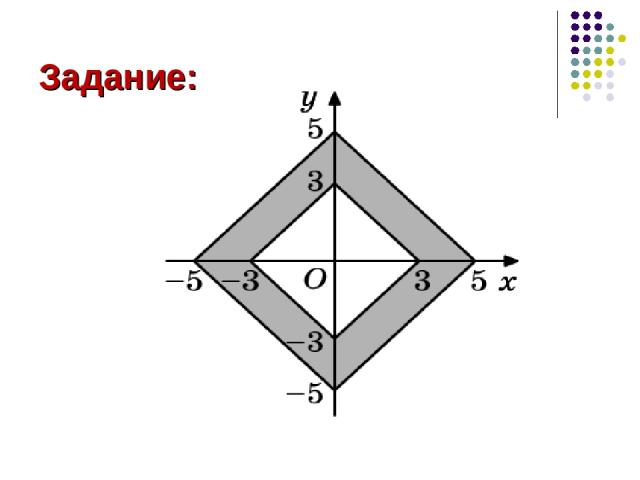
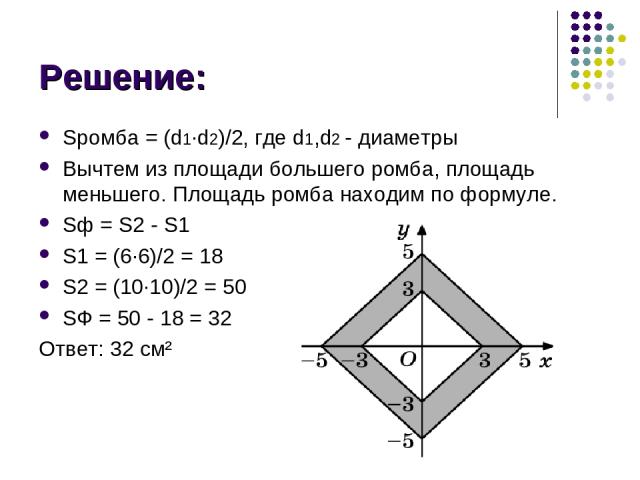
Задание:

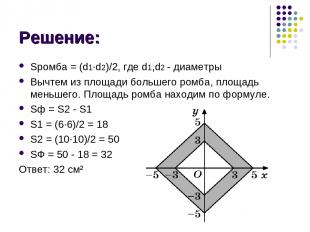
Решение: Sромба = (d1∙d2)/2, где d1,d2 - диаметры Вычтем из площади большего ромба, площадь меньшего. Площадь ромба находим по формуле. Sф = S2 - S1 S1 = (6∙6)/2 = 18 S2 = (10∙10)/2 = 50 SФ = 50 - 18 = 32 Ответ: 32 см²

Работа по группам 1,2,3 группы решают задачи В6, В9, В11 4,5 группы решают задачи С2

Теория Задание В6. Основы геометрии. Чаще всего встречаются задания на решение треугольников, но знать надо все фигуры планиметрии. Необходимые знания: виды треугольников; понятия биссектрисы, медианы, высоты; тригонометрические функции и их значения; основное тригонометрическое тождество; формулы приведения; теорема Пифагора. И помните при правильном решении ответ получается точно без корня.

Типичные ошибки при решении задания В6 в ЕГЭ выпускник чаще всего может перепутать катет с гипотенузой; выпускник чаще всего не знает или неверно записывает отношение сторон при использовании тригонометрических функций;

Задания для решения Задача 1 Задача 2 Задача 4 Задача 3 Задача 5

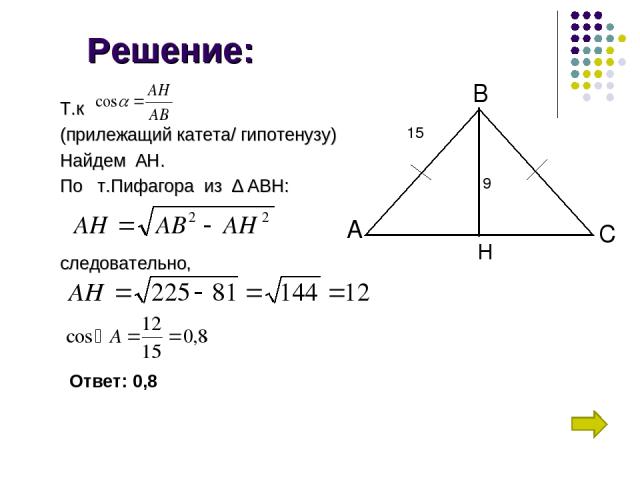
Задача 1 В равнобедренном треугольнике ABC c основанием AC боковая сторона АВ равна 15,а высота, проведенная к основанию, равна 9. Найдите косинус угла А.

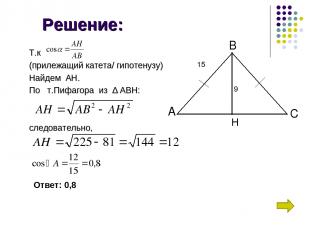
Решение: Т.к (прилежащий катета/ гипотенузу) Найдем АН. По т.Пифагора из ∆ АВН: следовательно, А С В H 15 9 Ответ: 0,8

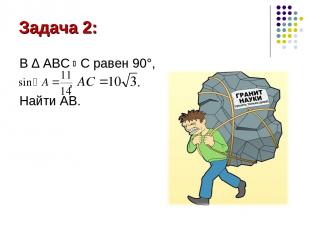
Задача 2: В ∆ АВС С равен 90°, , . Найти АВ.

Решение: А В С Нам известен прилежащий катет, следовательно, зная синус угла А можно найти его косинус. По основному тригонометрическому тождеству: По определению косинуса : Ответ: 28 ;

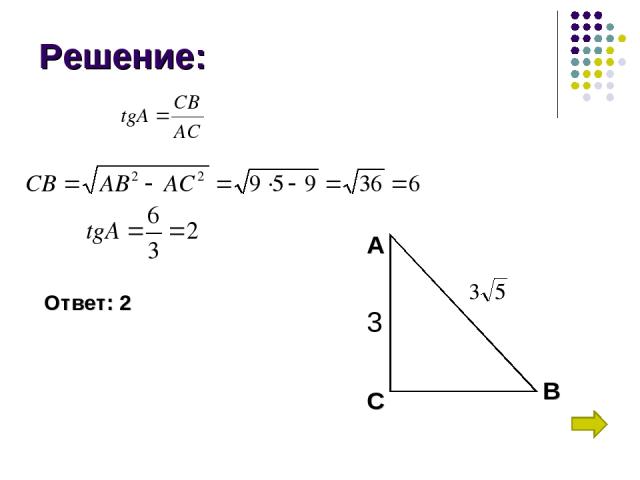
Задача 3: В треугольнике АВС угол С равен 90°, , AC = 3. Найдите tg A.

Решение: С А В 3 Ответ: 2

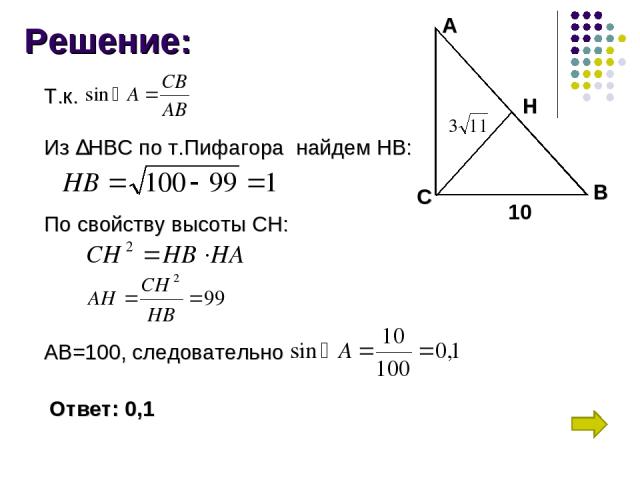
Задача 4: В треугольнике АВС угол С равен 90°, СН-высота,ВС=10, СН = . Найти sin A.

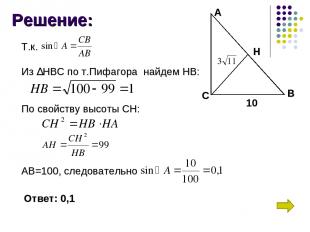
Решение: А В С Н 10 Т.к. Из ∆НВС по т.Пифагора найдем НВ: По свойству высоты СН: АВ=100, следовательно Ответ: 0,1

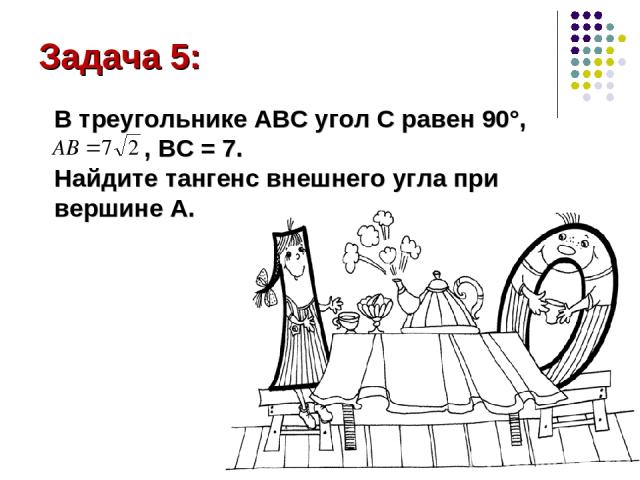
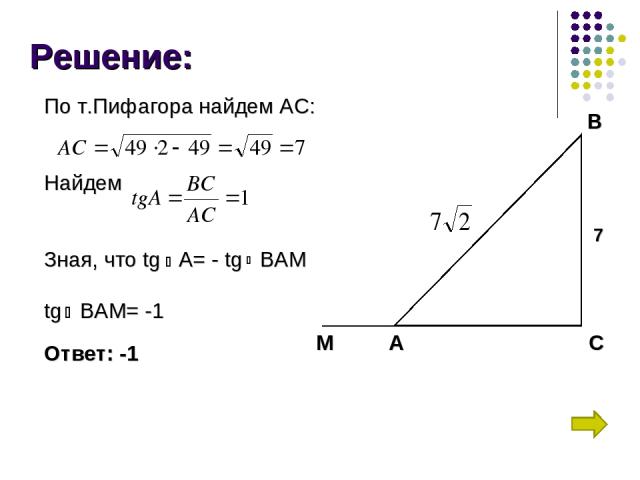
Задача 5: В треугольнике АВС угол С равен 90°, , ВС = 7. Найдите тангенс внешнего угла при вершине А.

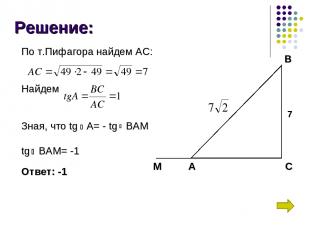
Решение: По т.Пифагора найдем АС: Найдем Зная, что tg A= - tg BAM tg BAM= -1 Ответ: -1

Решение задач типа В9

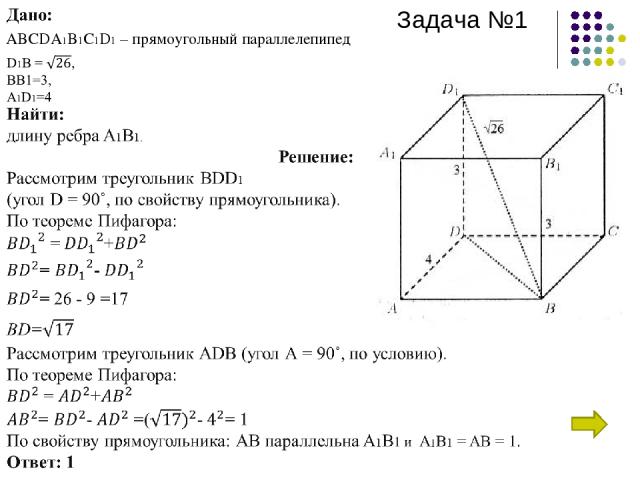
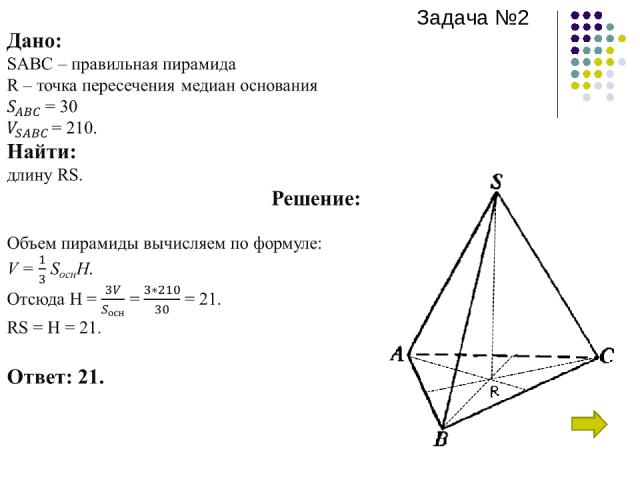
Задача №1. В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что D1B= , BB1=3, A1D1=4. Найти длину ребра A1B1. Посмотреть решение. Задача №2. В правильной треугольной пирамиде SABC медианы основания пересекаются в точке R. Площадь треугольника ABC равна 30, объем пирамиды равен 210. Найдите длину отрезка RS. Посмотреть решение. Задача №3. Найдите квадрат расстояния между вершинами B и D1 прямоугольного параллелепипеда ABCDA1B1C1D1, для которого AB=4, AD=6,AA1=5. Посмотреть решение.

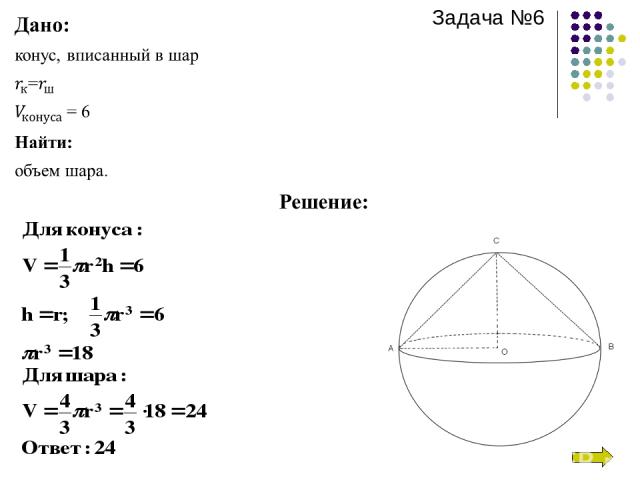
Задача № 4. Осевое сечение конуса- равносторонний треугольник, площадь которого равна . Найти высоту конуса. Посмотреть решение. Задача № 5. Дано два цилиндра. Объем первого равен 12 м³ . Радиус основания второго в два раза меньше, чем первого, а высота в три раза больше. Требуется найти объем второго цилиндра. Посмотреть решение. Задача № 6. Конус вписан в шар. Радиус основания конуса равен радиусу основания шара. Объем конуса равен 6. Найдите объем шара. Посмотреть решение.

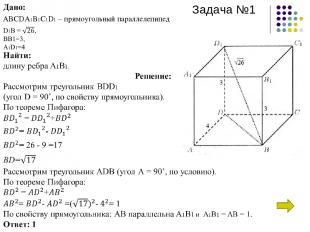
ABCDA1B1C1D1 – прямоугольный параллелепипед Задача №1

Задача №2

Задача №3

Задача №4

Задача №5

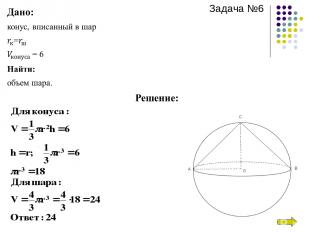
Задача №6

Задания В11 Задача 1 Задача 2

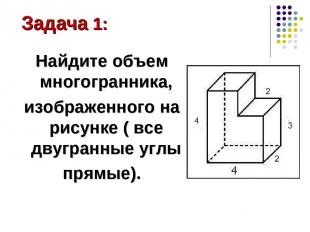
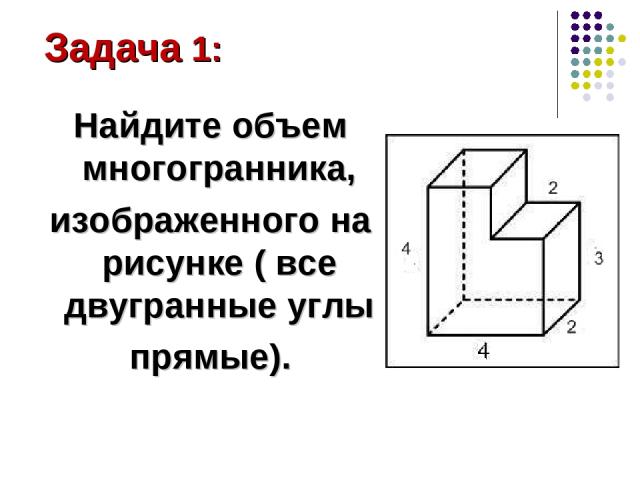
Найдите объем многогранника, изображенного на рисунке ( все двугранные углы прямые). Задача 1:

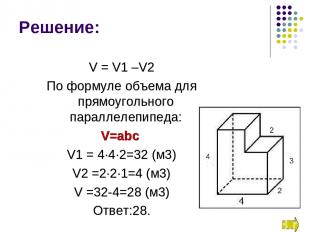
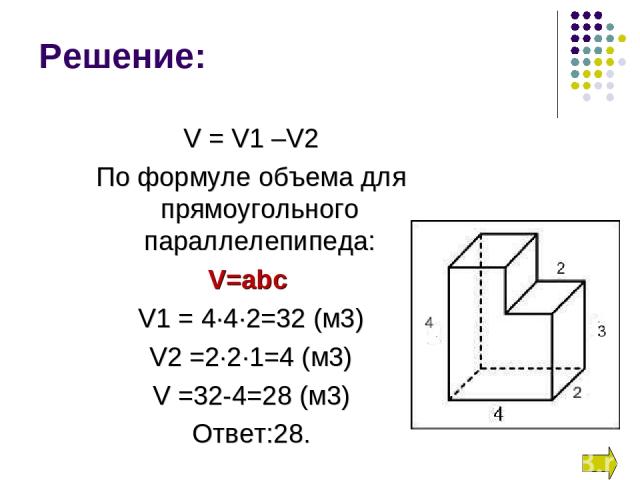
V = V1 –V2 По формуле объема для прямоугольного параллелепипеда: V=abc V1 = 4∙4∙2=32 (м3) V2 =2∙2∙1=4 (м3) V =32-4=28 (м3) Ответ:28. Решение:

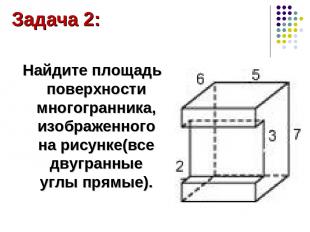
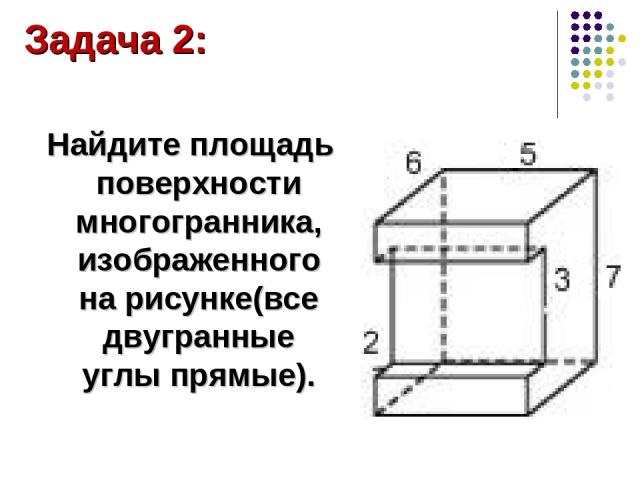
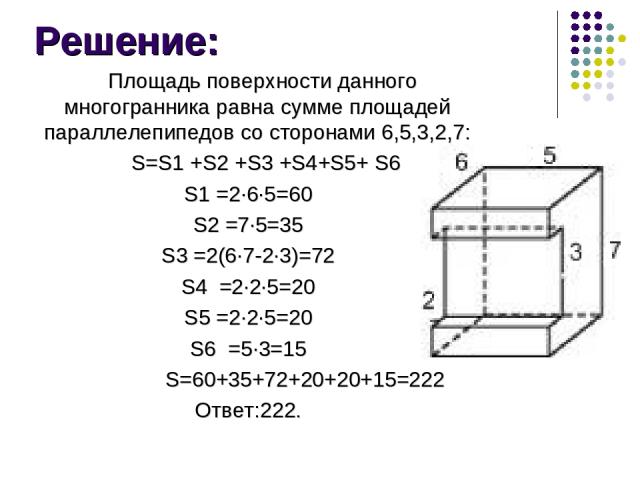
Найдите площадь поверхности многогранника, изображенного на рисунке(все двугранные углы прямые). Задача 2:

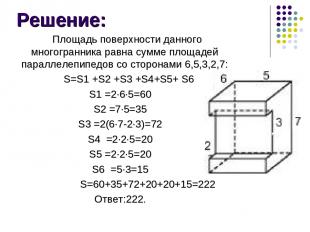
Решение: Площадь поверхности данного многогранника равна сумме площадей параллелепипедов со сторонами 6,5,3,2,7: S=S1 +S2 +S3 +S4+S5+ S6 S1 =2∙6∙5=60 S2 =7∙5=35 S3 =2(6∙7-2∙3)=72 S4 =2∙2∙5=20 S5 =2∙2∙5=20 S6 =5∙3=15 S=60+35+72+20+20+15=222 Ответ:222.

Задачи С2:

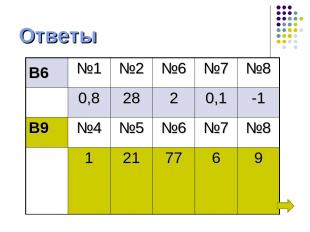
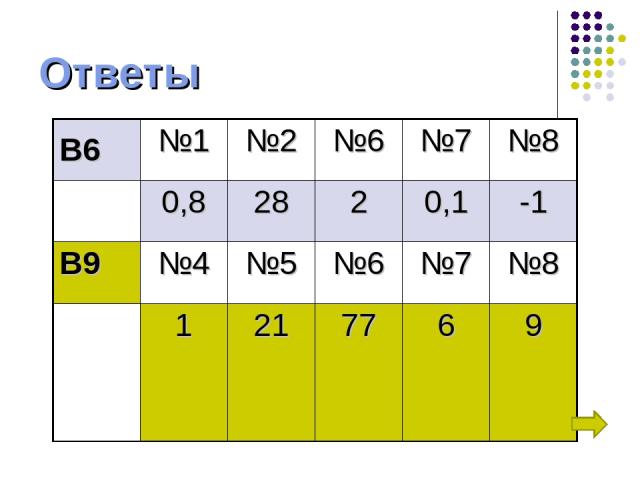
Ответы В6 №1 №2 №6 №7 №8 0,8 28 2 0,1 -1 В9 №4 №5 №6 №7 №8 1 21 77 6 9

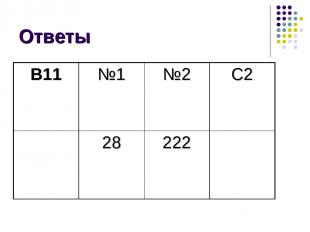
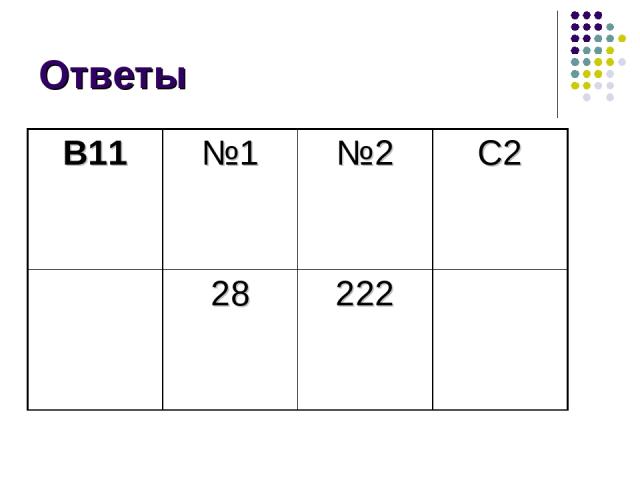
Ответы В11 №1 №2 С2 28 222

В создании презентации принимали участие выпускники 2012 года: Киселева Анастасия, Трубин Александр, Соловьев Вадим, Макарова Юлия, Кривда Алина, Романовская Ольга, Швецова Ирина, Абрахина Дарья.