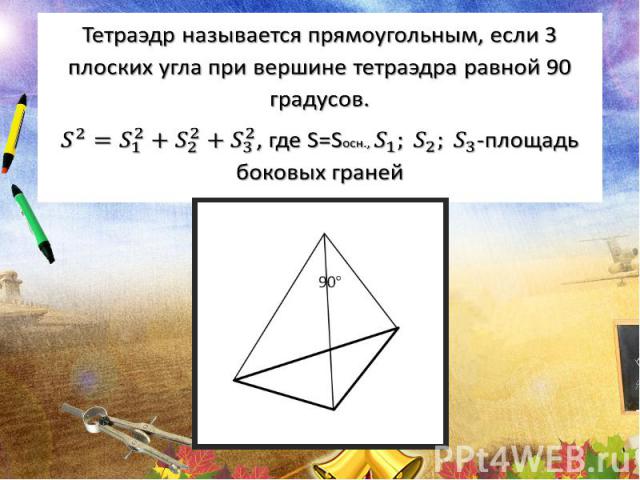
Презентация на тему: Геометрические задачи на экзаменах

Тема урока: «Геометрические задачи на экзаменах»

Ход урока:

Решение задач для класса

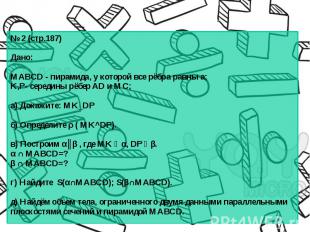
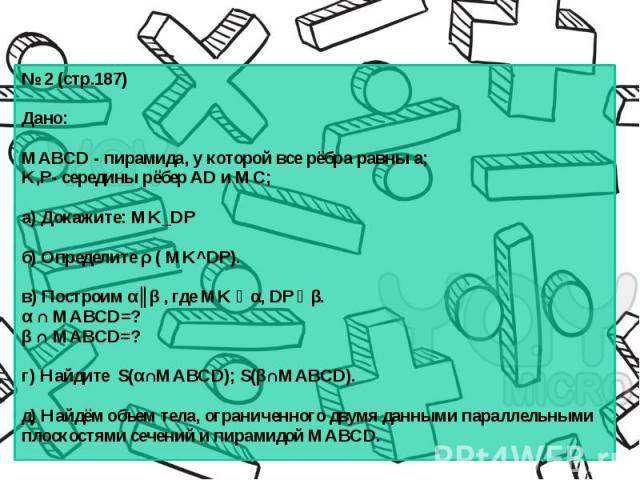
№ 2 (стр.187) № 2 (стр.187) Дано: MABCD - пирамида, у которой все рёбра равны а; K,P- середины рёбер AD и MC; а) Докажите: MK_DP  б) Определите ρ ( MK^DP). в) Построим α║β , где MK ϵ α, DP ϵ β. α ∩ MABCD=? β ∩ MABCD=? г) Найдите S(α∩MABCD); S(β∩MABCD). д) Найдём объем тела, ограниченного двумя данными параллельными плоскостями сечений и пирамидой MABCD.

№ 3 (стр.226) № 3 (стр.226) В основании прямой призмы лежит параллелограмм, сторона которого равна 4. Синус острого угла параллелограмма равен √3/4. Отношение площадей разных сечений, проходящей через сторону нижнего основания и сторону верхнего основания, к площади основания призмы равно 4/5 и 3/5. Найдите объём призмы.

Минутка релаксации

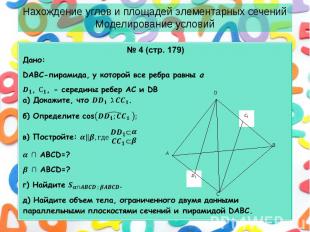
№ 6 (стр.205) № 6 (стр.205) Стороны основания треугольной пирамиды равны 13, 14 и 15. Боковые рёбра одинаково наклонены к плоскости основания под углом 60°. В пирамиду вписана прямая треугольная призма, три вершины которой принадлежат боковым рёбрам пирамиды. Найдите отношения площадей оснований пирамиды и призмы наибольшего объема.

Задачи-ловушки

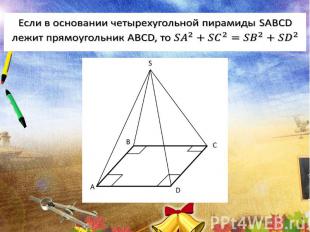
Домашнее задание: Уровень А

Домашнее задание: Уровень B

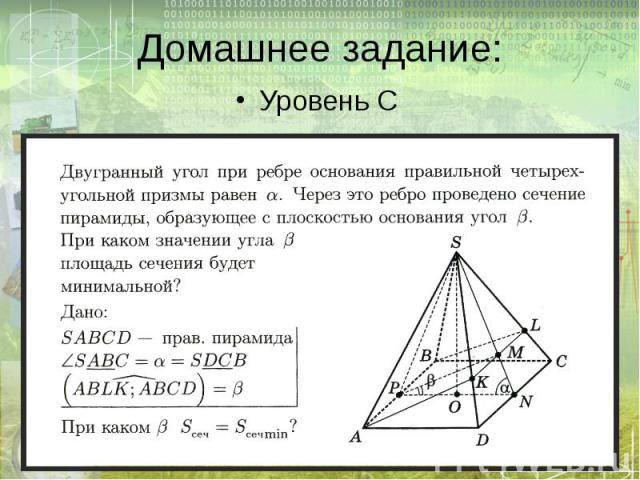
Домашнее задание: Уровень C

Рисунки в пространстве

Фрактальная геометрия