Презентация на тему: Вписанные углы

Угол вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом. Вписанный АВС опирается на АМС. Угол вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом. Вписанный АВС опирается на АМС.

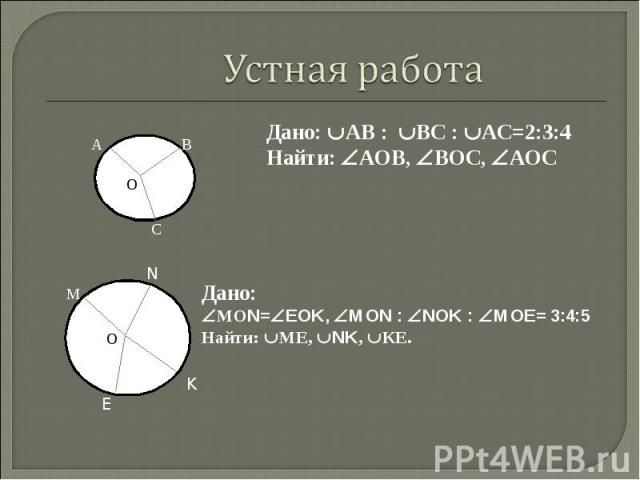
Пусть АВС – вписанный угол окружности с центром О, опирающийся на АС. Докажем, что АВС = половине АС (на которую он опирается). Существует 3 возможных случая расположения луча ВО относительно АВС. Рассмотрим их. Пусть АВС – вписанный угол окружности с центром О, опирающийся на АС. Докажем, что АВС = половине АС (на которую он опирается). Существует 3 возможных случая расположения луча ВО относительно АВС. Рассмотрим их.

Например луч совпадает со стороной ВС в этом случае АС меньше полуокружности, поэтому АОС= АС. Так как АОС внешний угол равнобедренного АВО, а 1 и 2 при основании равнобедренного треугольника равны, то АОС = 1+ 2 = 2 1. Отсюда следует, что 2 1 = АС или АВС = 1 = 1/2 АС. Например луч совпадает со стороной ВС в этом случае АС меньше полуокружности, поэтому АОС= АС. Так как АОС внешний угол равнобедренного АВО, а 1 и 2 при основании равнобедренного треугольника равны, то АОС = 1+ 2 = 2 1. Отсюда следует, что 2 1 = АС или АВС = 1 = 1/2 АС.

В этом случае луч ВО пересекает АС в некоторой точке D. Точка D разделяет АС на две дуги: АD и DC. По доказанному в п.1 АВD = 1/2 AD и DBC= 1/2 DC. Складывая эти равенства попарно, получаем: ABD + DBC = 1/2 АD + 1/2 DC, или АВС= 1/2 АС. В этом случае луч ВО пересекает АС в некоторой точке D. Точка D разделяет АС на две дуги: АD и DC. По доказанному в п.1 АВD = 1/2 AD и DBC= 1/2 DC. Складывая эти равенства попарно, получаем: ABD + DBC = 1/2 АD + 1/2 DC, или АВС= 1/2 АС.

АВD равнобедренный, AOD - внешний, т.к. ABD - равнобедр. То 1 = 2 => AOD = 1 + 2 = 2 1 = AD, следовательно ABD = 1/2 AD. АВD равнобедренный, AOD - внешний, т.к. ABD - равнобедр. То 1 = 2 => AOD = 1 + 2 = 2 1 = AD, следовательно ABD = 1/2 AD. Аналогично: ВСО равнобедр. COD - внешний, следовательно СВD= 1/2 CD. Следовательно, АВС=1/2 АС

Вписанные углы , опирающиеся на одну и ту же дугу, равны. Вписанные углы , опирающиеся на одну и ту же дугу, равны.

Вписанный угол, опирающийся на полуокружность прямой. Вписанный угол, опирающийся на полуокружность прямой.