Презентация на тему: Геометрические построения на плоскости

Исследовательскаяработапо геометрии на тему:«Геометрические построения на плоскости».

Цель: Исследование роли «геометрического построения на плоскости» в геометрии и архитектуре. Задачи: 1.Изучить научную литературу, ресурсы сети Интернет по исследуемой теме.2.Выявить роль задач на построение сечений в геометрии, архитектуре.3.Показать:а) непосредственную связь геометрии и архитектуры.б) прикладные возможности задач на построение сечений.в) значимость задач в развитии современной науки.

1. Введение.2. Из истории начертательной геометрии.3. Виды проецирования. 1) центральное проецирование; 2) параллельное проецирование; 3) основные независимые свойства параллельного проецирования.4. Пересечение многогранников плоскостью. 1) методы построения сечений многогранников: - метод следов; - решение задач на построение сечений многогранников; - способ внутреннего проектирования; - решение задач на построение сечений многогранников.5. Конические сечения. 1) ранняя история; 2) построение конических сечений: - эллипс; - гипербола; - парабола. 3) свойства конических сечений: - определения Папа; - конструкция Данделена; - другие свойства. 4) аналитический подход: - алгебраическая классификация; - вывод уравнений конических сечений. 5) проективный подход; 6) специальные построения;6. Заключение.7. Список используемой литературы

Введение.

Из истории начертательной геометрии Гаспар МонжСергей Курдюмов

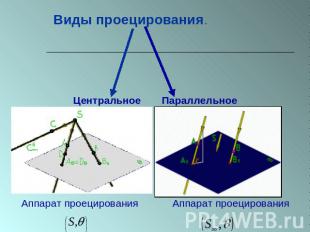
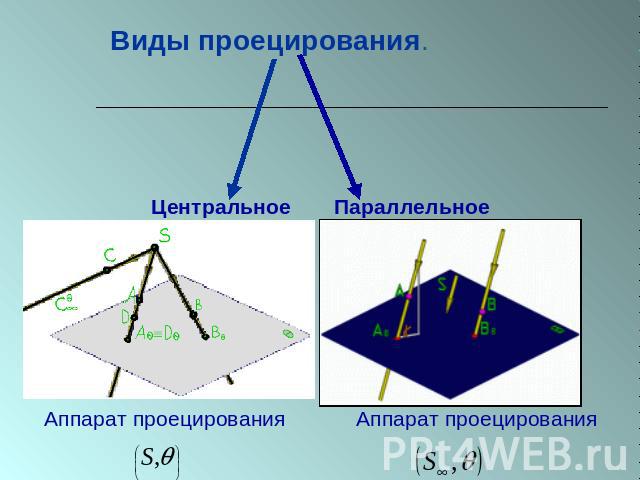
Виды проецирования. ЦентральноеПараллельное Аппарат проецирования Аппарат проецирования

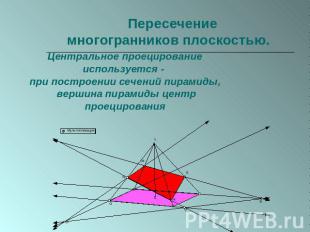
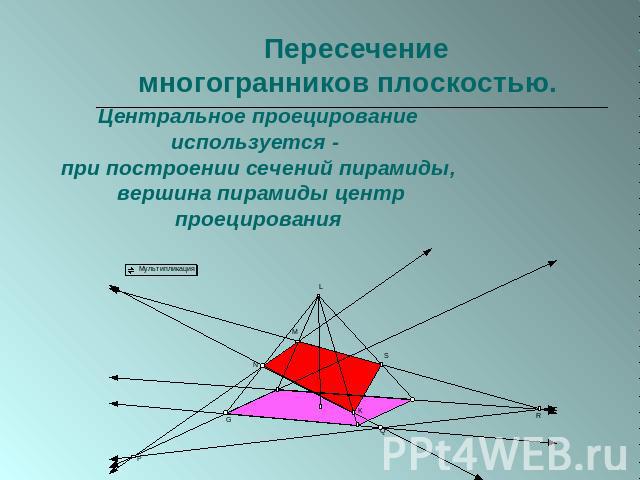
Пересечение многогранников плоскостью. Центральное проецирование используется - при построении сечений пирамиды, вершина пирамиды центр проецирования

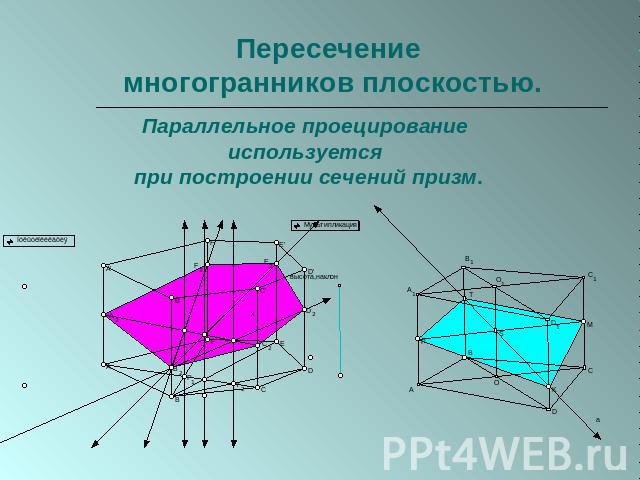
Пересечение многогранников плоскостью. Параллельное проецирование используется при построении сечений призм.

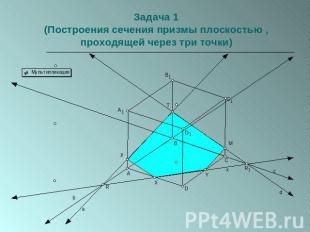
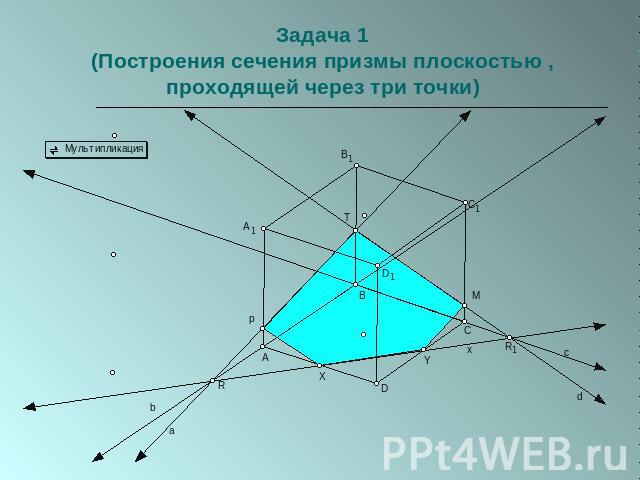
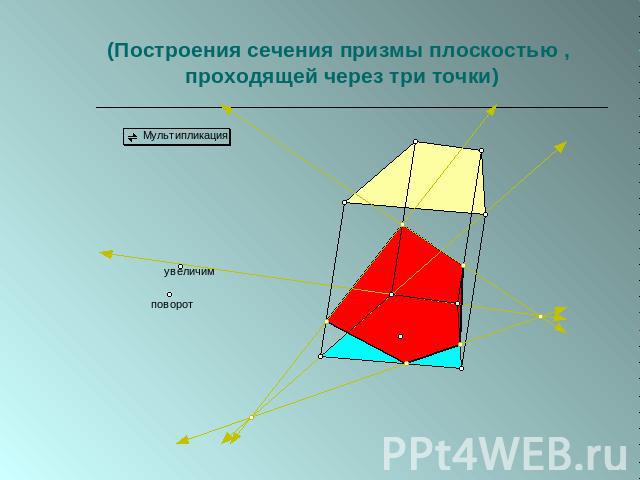
Задача 1(Построения сечения призмы плоскостью , проходящей через три точки)

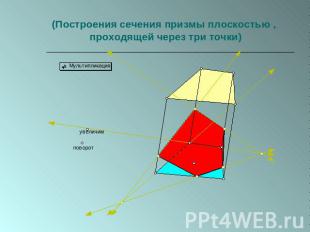
(Построения сечения призмы плоскостью , проходящей через три точки)

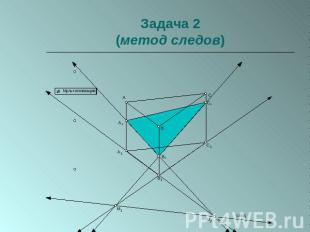
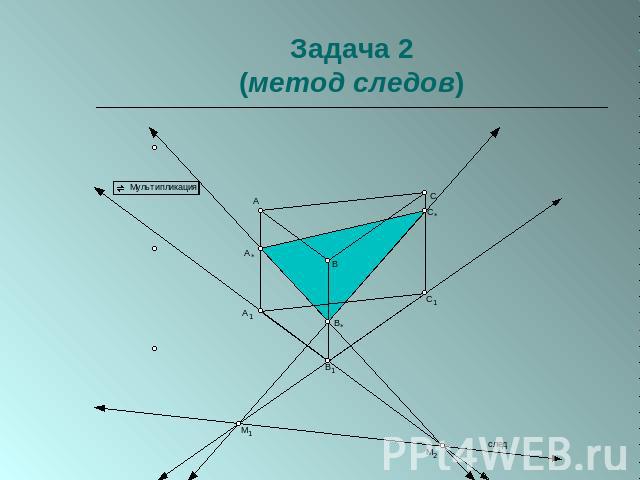
Задача 2(метод следов)

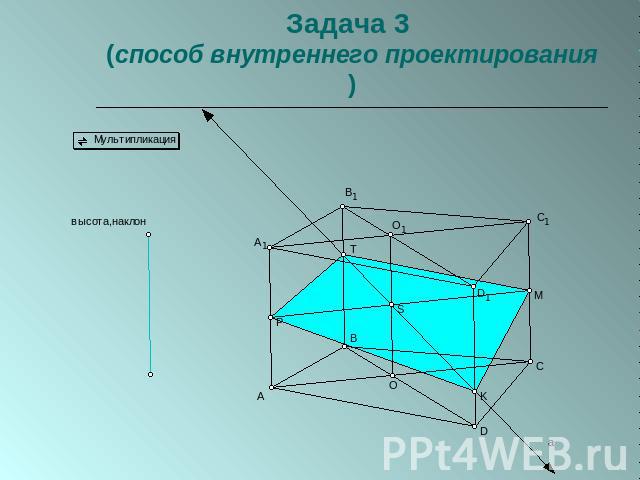
Задача 3 (способ внутреннего проектирования)

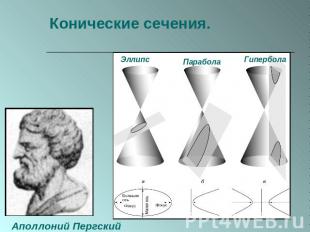
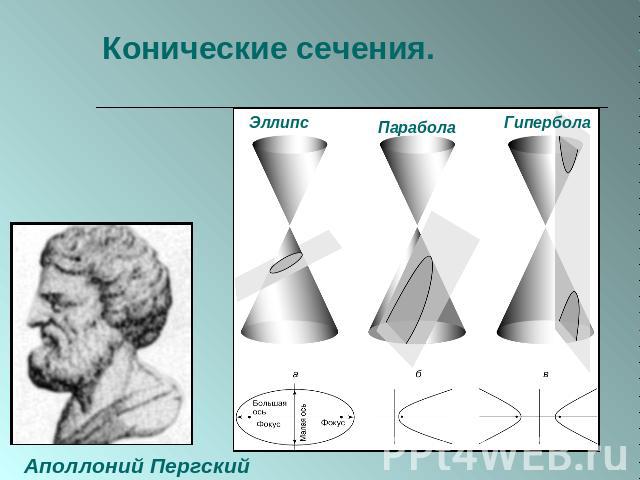
Конические сечения. Аполлоний Пергский

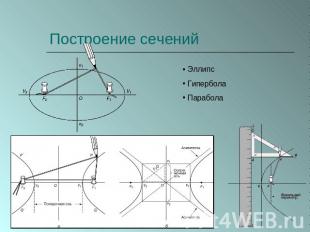
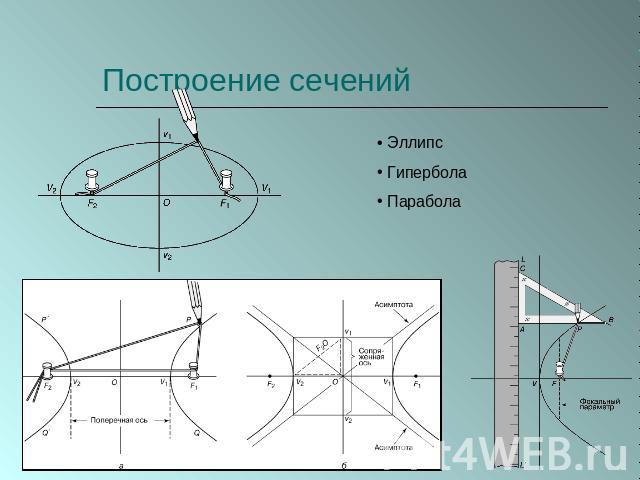
Построение сечений Эллипс Гипербола Парабола

Аналитический подход

Проективный подход

ЗАКЛЮЧЕНИЕГеометрия в архитектуре

Искусство не есть одна наука, искусство пользуется наукой , искусство должно уметь законы и знания применять к делу(П.П.Чистяков.)

Список используемой литературы 1. А.В. Бубенков, М.Я. Громов (Начертательная геометрия); 2. С. А. Фролов (Начертательная геометрия);3. А.А. Беклемшнева (Сборник задач по аналитической геометрии и линейной алгебре ).4. Ресурсы сети Интернет: а) www.yandex.ru б) www.google.com