Презентация на тему: Двумерный симплекс история его изучения

Двумерный симплекс история его изучения Выполнила: ученица 8 Б класса МОУ СОШ № 29 г. Ставрополя НИКИТИНА АЛЕНА

На уроках геометрии в 7 классе мы изучали треугольник и его свойства. Небольшие исторические справки к изучаемому материалу показали, что знание об этой фигуре развивалось постепенно. Не мало ученых изучали треугольник, формулировали новые задачи, открывали свойства и создалось впечатление, что изучение треугольника еще не завершено и возможны еще новые открытия. Многие факты остались за страницами школьного учебника и мы попытались приоткрыть некоторые тайны.

ЦЕЛЬ МОЕГО ПРОЕКТА Изучить материалы и существующую литературу по данному вопросу. Понять роль этой геометрической фигуры в человеческой деятельности. Создать исторический фон, соотнести материал изучаемый в школьном курсе с историей развития человечества.

Работая над проектом, я искала информацию в справочниках, энциклопедиях и в Интернете. Некоторые факты показавшиеся мне удивительными отражены в моей презентации

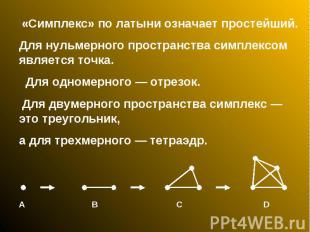
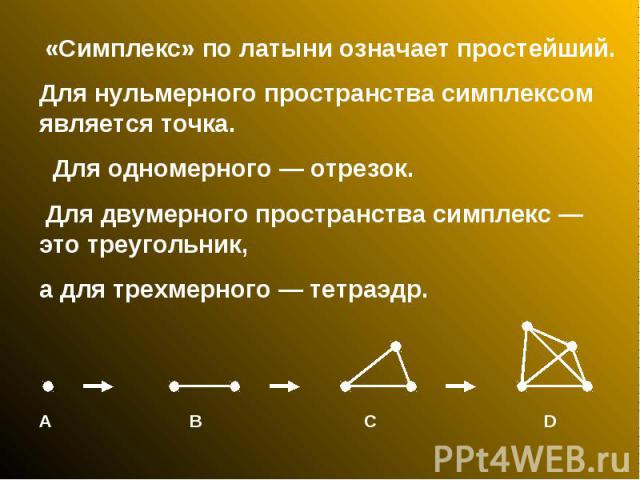
«Симплекс» по латыни означает простейший. Для нульмерного пространства симплексом является точка. Для одномерного — отрезок. Для двумерного пространства симплекс — это треугольник, а для трехмерного — тетраэдр.

Треугольник – это простейшая фигура: три стороны и три вершины

Именно в силу своей простоты треугольник явился основой многих измерений. Землемеры при своих вычислениях площадей земельных участков и астрономы при нахождении расстояний до планет и звезд используют свойства треугольников.

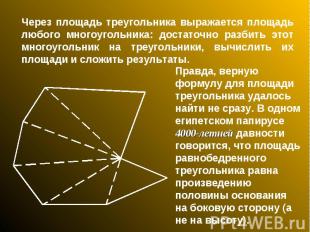
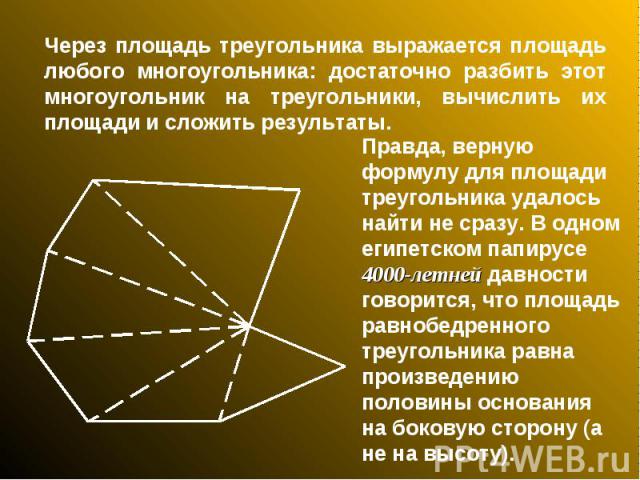
Через площадь треугольника выражается площадь любого многоугольника: достаточно разбить этот многоугольник на треугольники, вычислить их площади и сложить результаты. Правда, верную формулу для площади треугольника удалось найти не сразу. В одном египетском папирусе 4000-летней давности говорится, что площадь равнобедренного треугольника равна произведению половины основания на боковую сторону (а не на высоту).

Через 2000 лет в Древней Греции изучение свойств треугольника ведется очень активно. Пифагор открывает свою теорему. Герон Александрийский находит формулу, выражающую площадь треугольника через его стороны. Становится известным, что биссектрисы, как медианы и высоты, пересекаются в одной точке.

Особенно активно свойства треугольника исследовались в XV – XVI веках. Одна из красивейших теорем того времени принадлежала Леонарду Эйлеру: «Середины сторон треугольника, основания его высот и середины отрезков высот от вершины до точки их пересечения лежат на одной окружности» Эта окружность получила название «окружности девяти точек». Ее центр оказался в середине отрезка, соединяющего точку пересечения высот с центром описанной окружности

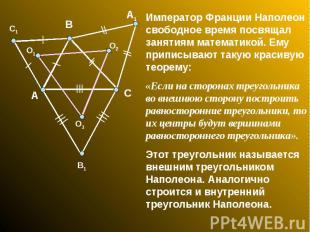
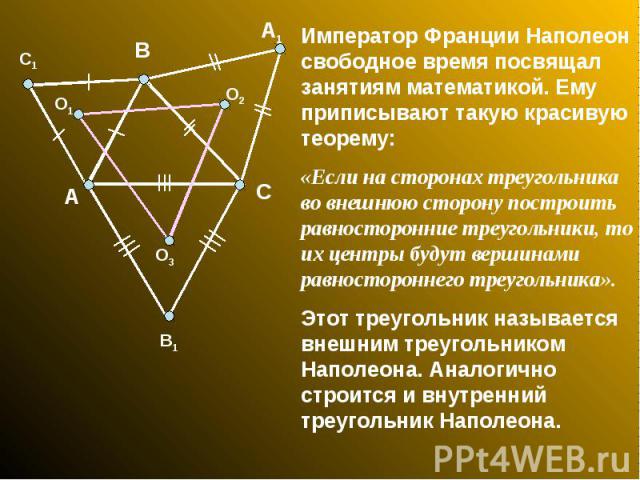
Император Франции Наполеон свободное время посвящал занятиям математикой. Ему приписывают такую красивую теорему: «Если на сторонах треугольника во внешнюю сторону построить равносторонние треугольники, то их центры будут вершинами равностороннего треугольника». Этот треугольник называется внешним треугольником Наполеона. Аналогично строится и внутренний треугольник Наполеона.

Огромное количество работ по геометрии треугольника, проведенное в XV – XIX веках, создало впечатление, что о треугольнике уже известно все. Тем удивительнее было открытие, сделанное американским математиком Ф. Морли. «Если в треугольнике провести через вершины лучи, делящие углы на три равные части, то точки пересечения смежных трисектрис углов являются вершинами равностороннего треугольника».

ЭТАПЫ РАЗВИТИЯ МАТЕМАТИКИ

ВЫВОДЫ: В результате проведенных исследований материалов по рассматриваемому вопросу я узнала, что Треугольник изучался на протяжении всего развития цивилизованного общества. «Задачи для оттачивания ума» были интересны не только ученым математикам, но и любителям и, даже, некоторым известным «нематематикам». Треугольник и его свойства проявляются во всех областях жизни человека: архитектуре, землемерии, астрономии, строительстве, химии, психологии, рекламе и т.д

Литература, которой я пользовалась: Энциклопедия для детей. Т.11. Математика. Главный редактор М.Д. Аксенова.- М:Аванта+,1999.-688с.: ил. Математика: Школьная энциклопедия. Гл. ред. С. М. Никольский. – М.: Большая Российская энциклопедия; Дрофа, 1997. – 527 с.: ил. Большая Советская Энциклопедия. Главный редактор Б.А. Введенский, том 4, второе издание, государственное научное издательство «Большая советская энциклопедия», 667с.