Презентация на тему: Статистические показатели

СТАТИСТИКА I (теория статистики) Часть 4. Статистические показатели.

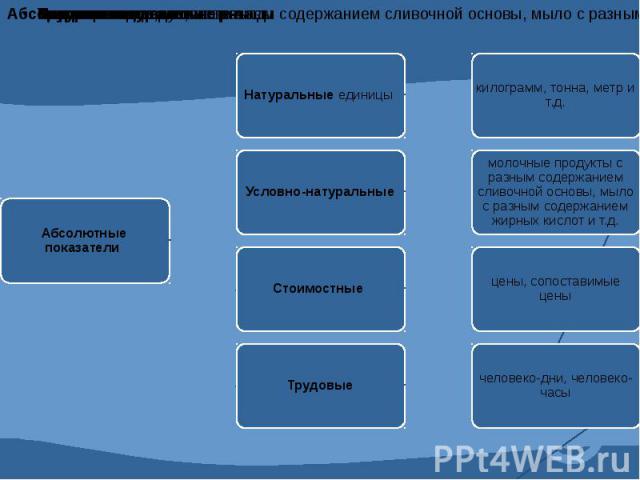
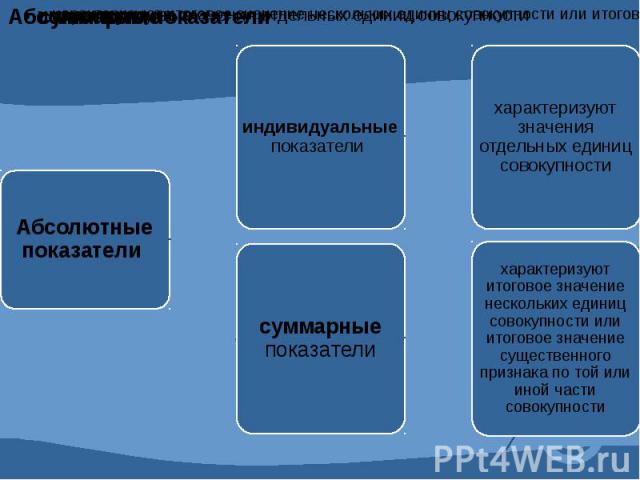
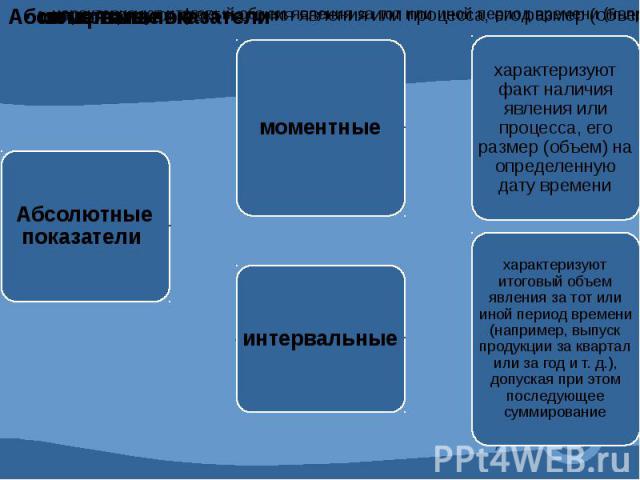
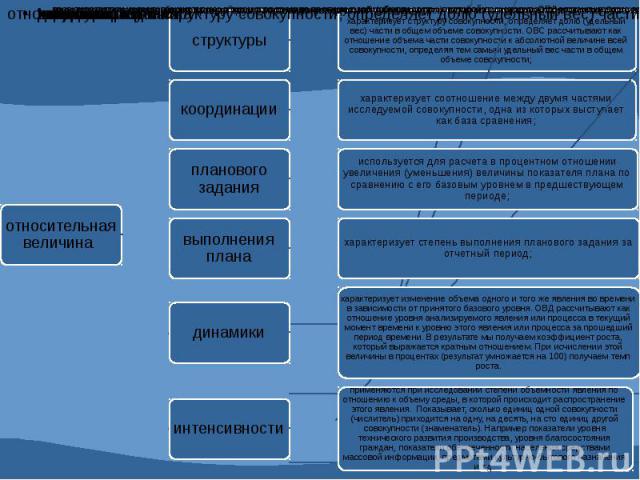
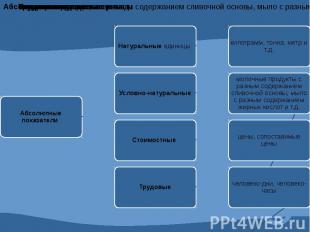
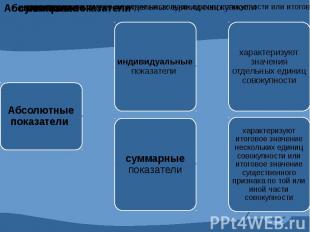
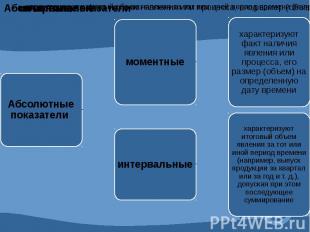
4.1 Абсолютные и относительные показатели. Абсолютные показатели характеризуют итоговую численность единиц совокупности или ее частей, размеры (объемы, уровни) изучаемых явлений и процессов, выражают временные характеристики. Относительные показатели - это цифровые обобщающие показатели, они есть результат сопоставления двух статистических величин.

4.2 Средние величины и их графические изображения. Средней величиной называют показатель, который характеризует обобщен- ное значение признака или группы признаков в исследуемой совокупности.

В статистике соблюдаются следующие принципы применения сред­них величин. 1. Необходим обоснованный выбор статистической совокупности, для которой определяется средняя величина. 2.    При определении средней величины исходят из качественного содержания статистических величин, учитывая возможную взаимосвязь изучаемых признаков. 3.    Средняя величина должна рассчитываться по однородной сово­купности, которая позволяет применять метод группировки, предпола­гающий расчет системы обобщающих показателей. 4.    Общая средняя величина должна подкрепляться и поясняться групповыми средними величинами.

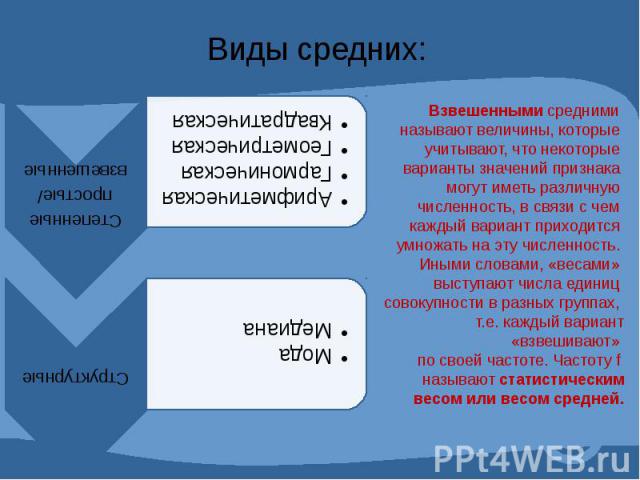
Средняя арифметическая - самый распространенный вид средней. Она используется, когда расчет осуществляется по не сгруппированным статистическим данным, где нужно получить среднее слагаемое. Средняя арифметическая - это такое среднее значение признака, при получении которого сохраняется неизменным общий объем признака в совокупности.

Средняя гармоническая. Эту среднюю называют обратной средней арифметической.

Средняя геометрическая. Чаще всего средняя геометрическая находит свое применение при определении средних темпов роста (средних коэффициентов роста), когда индивидуальные значения признака представлены в виде относительных величин. Она используется также, если необходимо найти среднюю между минимальным и максимальным значениями признака.

Средняя квадратическая величина. Основной сферой ее применения является измерение вариации признака в совокупности (расчет среднего квадратического отклонения).

Структурные средние

Показатели вариации Вариация — это различия индивидуальных значений признака у единиц изучаемой совокупности. Необходимость изучения вариации связана с тем, что средняя, являясь равнодействующей, выполняет свою основную задачу с разной степенью точности: чем меньше различия индивидуальных значений признака, подлежащих осреднению, тем однороднее совокупность, а, следовательно, точнее и надежнее средняя, и наоборот. Следовательно по степени вариации можно судить о границах вариации признака, однородности совокупности по данному признаку, типичности средней, взаимосвязи факторов, определяющих вариацию. Изменение вариации признака в совокупности осуществляется с помощью абсолютных и относительных показателей.

Абсолютные и относительные Абсолютные показатели вариации включают: размах вариации  среднее линейное отклонение  дисперсию  среднее квадратическое отклонение  Относительные показатели вариации включают: Коэффициент осцилляции  Относительное линейное отклонение (линейный коэффициент вариации)  Коэффициент вариации (относительное отклонение)

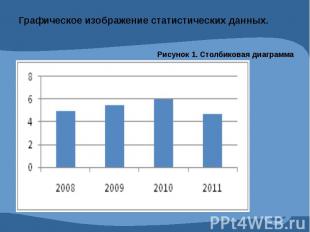
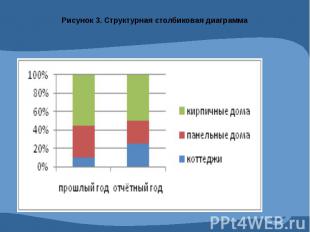
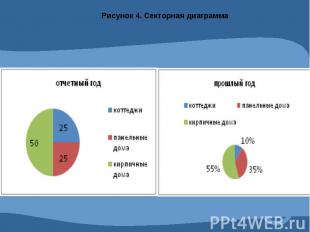
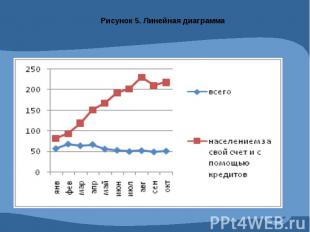
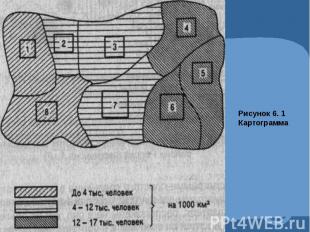
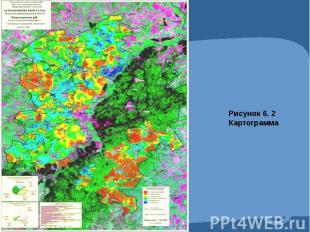
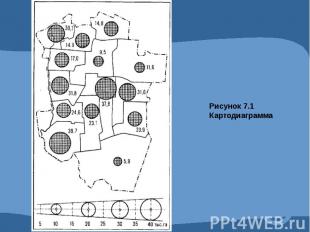
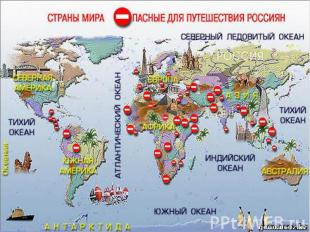
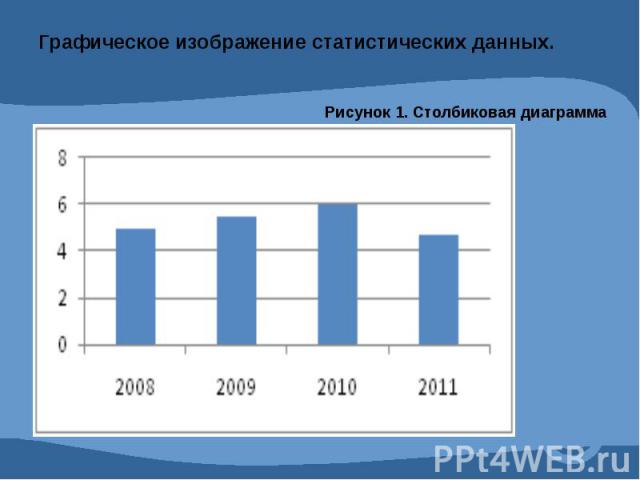
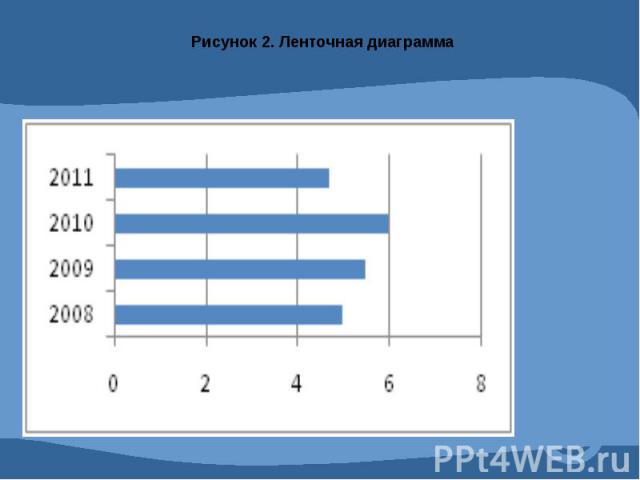
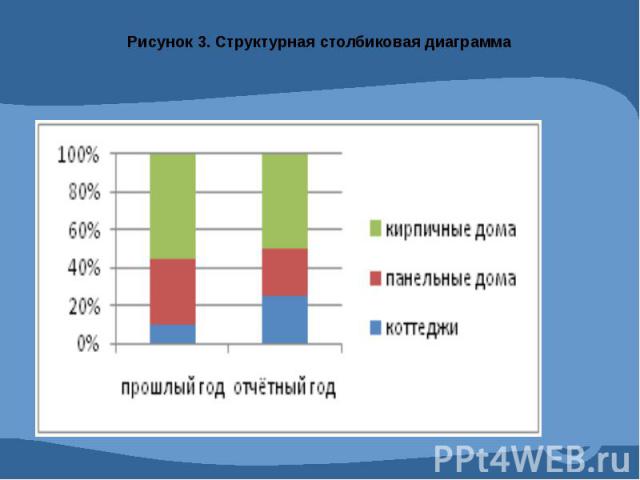
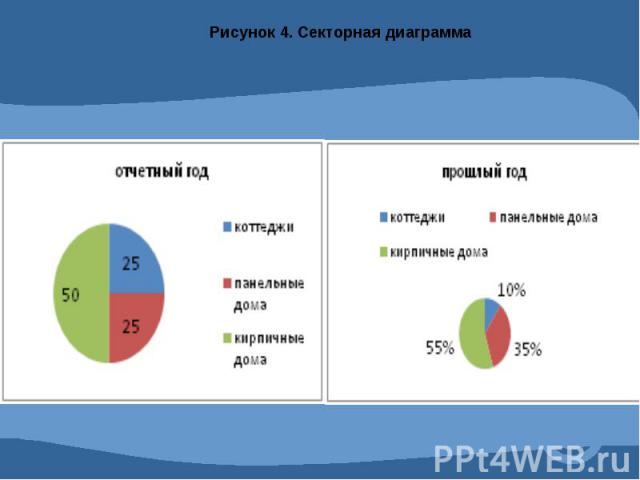
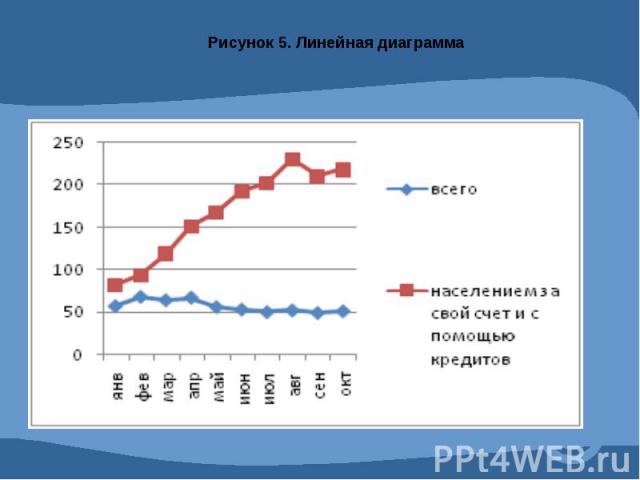
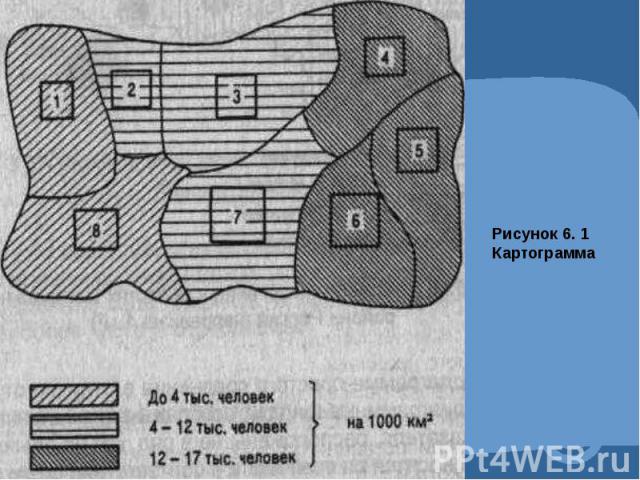
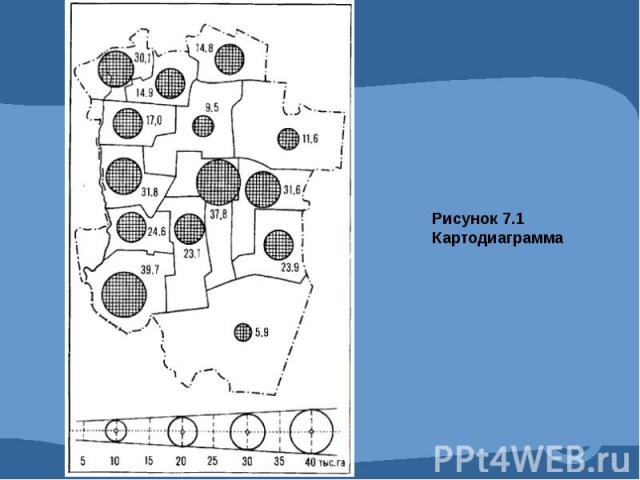
Графическое изображение статистических данных.