Презентация на тему: ычисление площадей плоских фигур с определенным интегралом


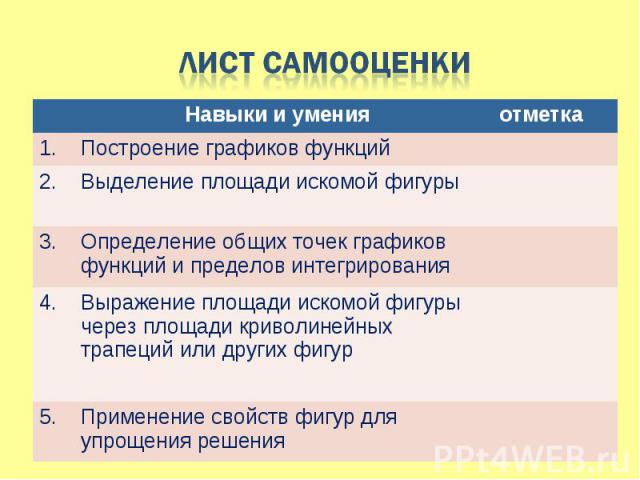
- обучающие: повторить и обобщить типы задач на вычисление площадей фигур, в том числе фигур сложной геометрической конфигурации,классифицировать задачи, систематизировать способы решения, скорретировать знания, познакомиться с историей развития интегрального исчисления; - обучающие: повторить и обобщить типы задач на вычисление площадей фигур, в том числе фигур сложной геометрической конфигурации,классифицировать задачи, систематизировать способы решения, скорретировать знания, познакомиться с историей развития интегрального исчисления; - развивающая: научить мыслить и оперировать математическими знаниями, стимулировать мышление учащихся; - воспитательная: развивать у учащихся коммуникативные компетенции (умение работать в группе, культуру общения), способствовать развитию интеллектуальной деятельности учащихся.

I. Блиц – опрос. Повторение основных теоретических знаний I. Блиц – опрос. Повторение основных теоретических знаний II. Практическое применение знаний III. Защита домашних задач IY. Постановка проблемы (обобщение) Y. Коррекция знаний по теме YI. Историческая справка YII. Подведение итогов YIII. Домашнее задание
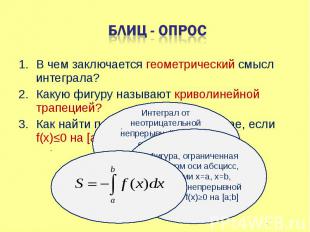
В чем заключается геометрический смысл интеграла? В чем заключается геометрический смысл интеграла? Какую фигуру называют криволинейной трапецией? Как найти площадь фигуры в случае, если f(x)≤0 на [a;b]?
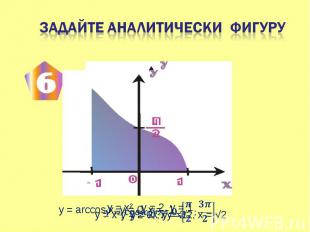
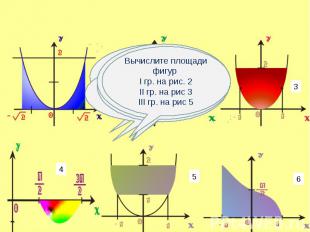
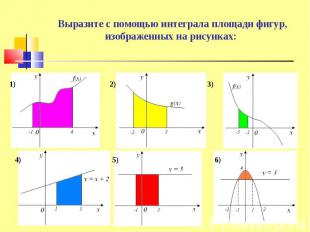



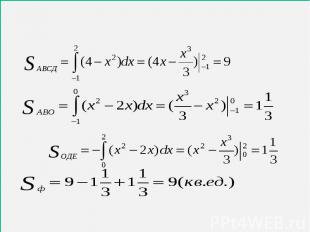
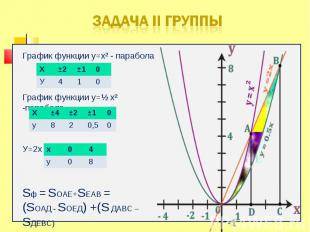

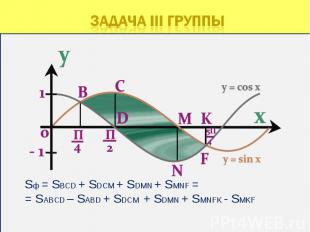


Проблема: Как с помощью интеграла вычислить площадь фигуры, не являющейся криволинейной трапецией? Проблема: Как с помощью интеграла вычислить площадь фигуры, не являющейся криволинейной трапецией? Задачи на вычисление площадей фигур с помощью интеграла можно классифицировать по виду геометрических фигур, площади которых необходимо вычислить
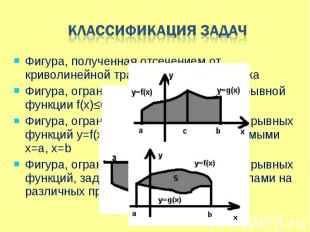
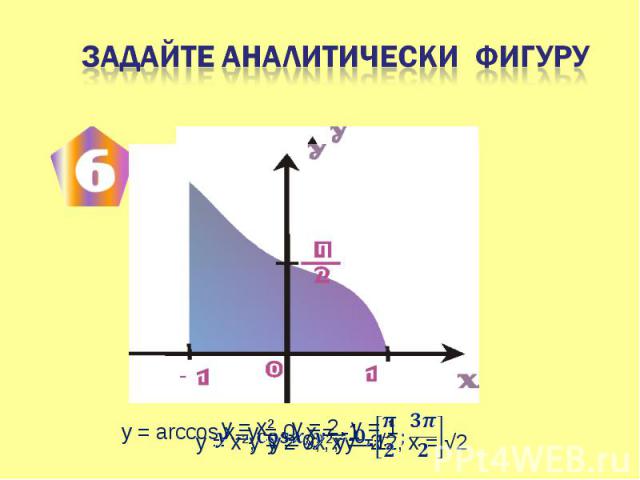
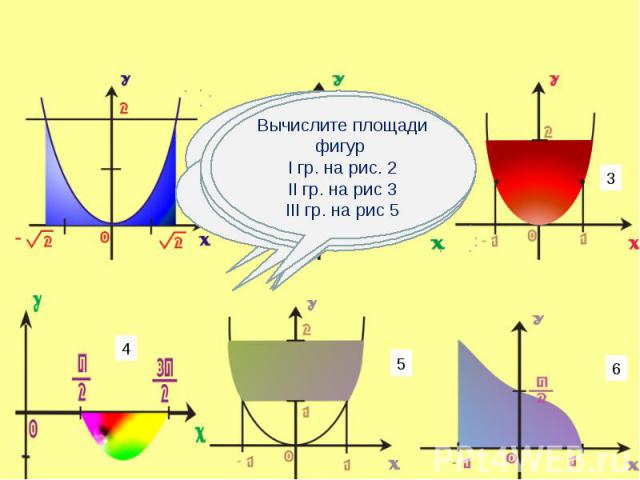
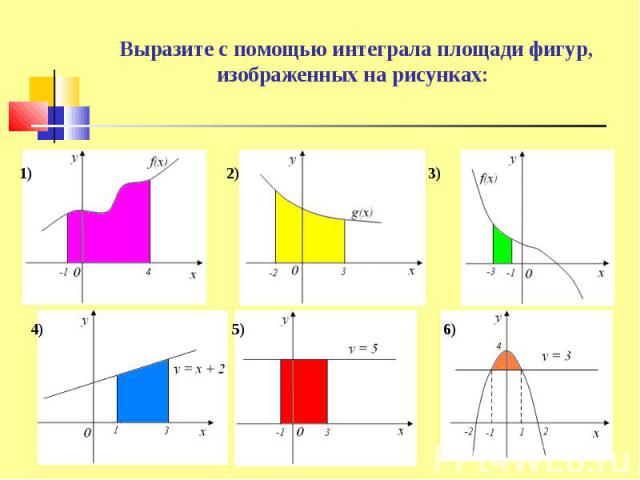
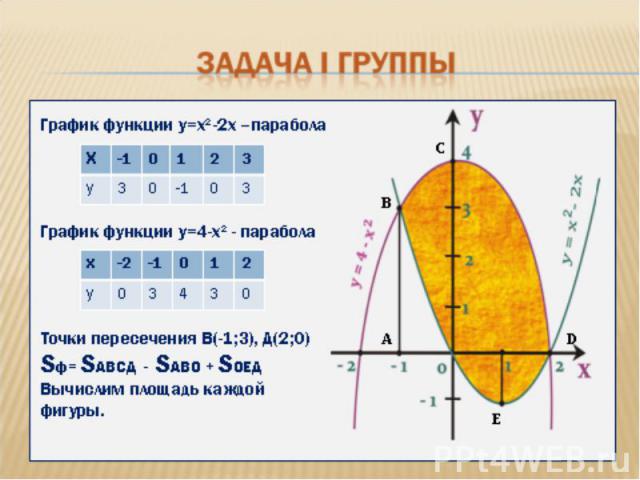
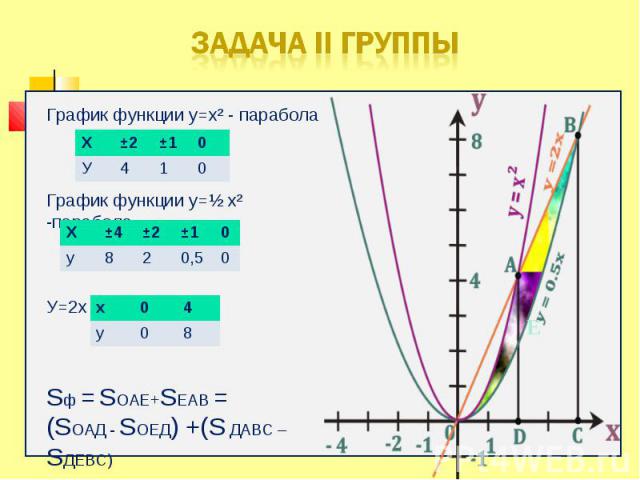
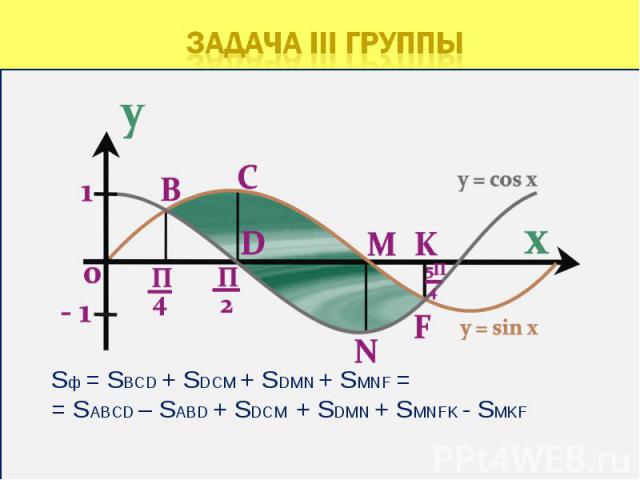
Фигура, полученная отсечением от криволинейной трапеции прямоугольника Фигура, полученная отсечением от криволинейной трапеции прямоугольника Фигура, ограниченная графиком непрерывной функции f(x)≤0 на [a;b] Фигура, ограниченная графиками непрерывных функций y=f(x), y=g(x), f(x)≥g(x) ≥0 и прямыми x=a, x=b Фигура, ограниченная графиками непрерывных функций, заданных различными формулами на различных промежутках


«Интеграл» придумал Якоб Бернулли (1690г.) «Интеграл» придумал Якоб Бернулли (1690г.) «восстанавливать» от латинского integro «целый» от латинского integer

Этот метод был подхвачен и развит Архимедом, и использовался для расчёта площадей парабол и приближенного расчёта площади круга. Этот метод был подхвачен и развит Архимедом, и использовался для расчёта площадей парабол и приближенного расчёта площади круга.



И. Ньютон И. Ньютон

Таким образом, уже Архимед успешно находил площади фигур, несмотря на то, что в математике его времени не было понятия интеграла Таким образом, уже Архимед успешно находил площади фигур, несмотря на то, что в математике его времени не было понятия интеграла Но лишь интегральное исчисление дает общий метод решения всех подобных задач Недаром даже поэты воспевали интеграл







![В чем заключается геометрический смысл интеграла? В чем заключается геометрический смысл интеграла? Какую фигуру называют криволинейной трапецией? Как найти площадь фигуры в случае, если f(x)≤0 на [a;b]? В чем заключается геометрический смысл интеграла? В чем заключается геометрический смысл интеграла? Какую фигуру называют криволинейной трапецией? Как найти площадь фигуры в случае, если f(x)≤0 на [a;b]?](https://fs1.ppt4web.ru/images/95377/156081/640/img3.jpg)


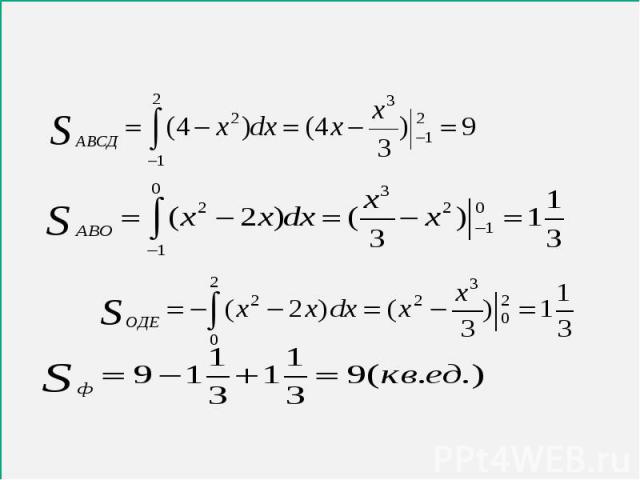



![Фигура, полученная отсечением от криволинейной трапеции прямоугольника Фигура, полученная отсечением от криволинейной трапеции прямоугольника Фигура, ограниченная графиком непрерывной функции f(x)≤0 на [a;b] Фигура, ограниченная графиками непрерывны… Фигура, полученная отсечением от криволинейной трапеции прямоугольника Фигура, полученная отсечением от криволинейной трапеции прямоугольника Фигура, ограниченная графиком непрерывной функции f(x)≤0 на [a;b] Фигура, ограниченная графиками непрерывны…](https://fs1.ppt4web.ru/images/95377/156081/640/img16.jpg)