Презентация на тему: Уравнения и неравенства

Многообразие видов уравнений и методов их решений во всех частях КИМ показательные; логарифмические; тригонометрические; иррациональные; уравнения, содержащие неизвестную в основании и показателе степени; комбинированные; уравнения с параметрами.

Формулировки заданий укажите промежуток, которому принадлежит корень уравнения; найдите сумму ( произведение) корней уравнения; укажите количество корней уравнения;

Неравенства в КИМах дробно-рациональные; логарифмические; показательные; степенные; иррациональные; комбинированные, содержащие функции разных видов.

Формулировки заданий решите неравенство; укажите множество решений неравенств; вычислите сумму всех натуральных решений неравенства; найдите наименьшее (наибольшее) целое число, удовлетворяющее неравенству и т.д.

1 2 -1 0 1. Укажите промежуток, содержащий корни уравнения. 2. Найдите сумму корней уравнения 3. Сколько корней имеет уравнение? 1. Решите неравенство 0 2 -1 -2 2. Найдите сумму чисел, удовлетворяющих неравенству 3. Найдите промежуток, содержащий наибольшее целое число, удовлетворяющее неравенству

Применение методов решения уравнений и неравенств

Способы решения систем уравнений подстановка сложение графически

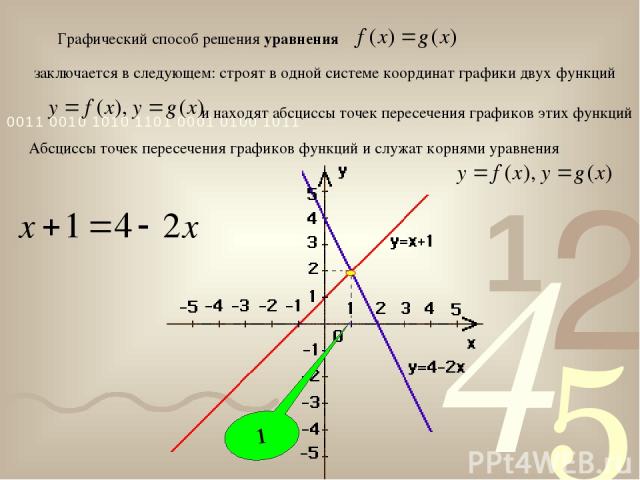
Абсциссы точек пересечения графиков функций и служат корнями уравнения Графический способ решения уравнения заключается в следующем: строят в одной системе координат графики двух функций и находят абсциссы точек пересечения графиков этих функций 1

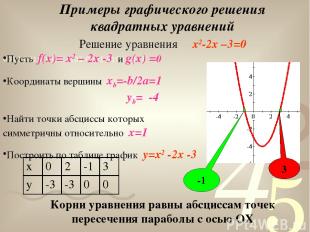
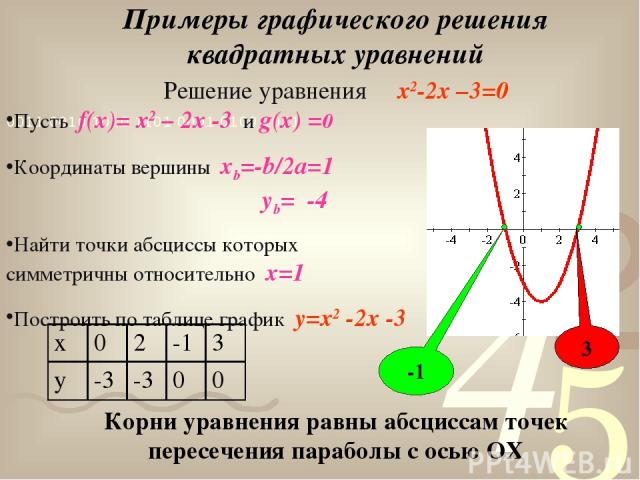
Пусть f(x)= x2 – 2x -3 и g(x) =0 Координаты вершины xb=-b/2a=1 yb= -4 Найти точки абсциссы которых симметричны относительно х=1 Построить по таблице график y=x2 -2x -3 Примеры графического решения квадратных уравнений 3 -1 Решение уравнения x2-2x –3=0 Корни уравнения равны абсциссам точек пересечения параболы с осью ОХ x 0 2 -1 3 y -3 -3 0 0

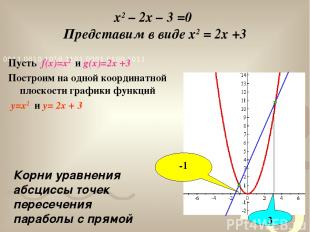
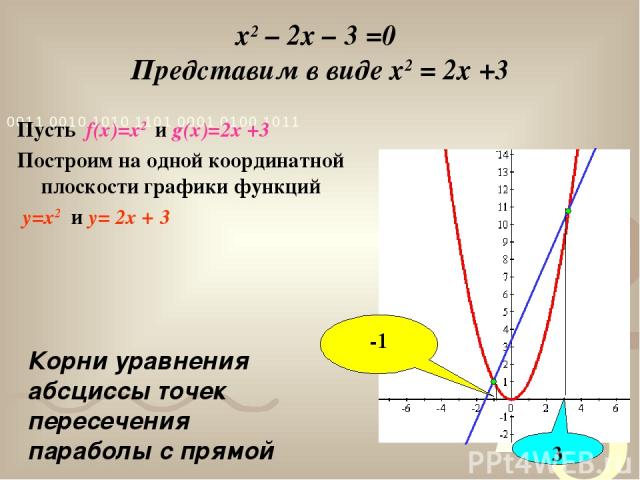
x2 – 2x – 3 =0 Представим в виде x2 = 2x +3 Пусть f(x)=x2 и g(x)=2x +3 Построим на одной координатной плоскости графики функций y=x2 и y= 2x + 3 3 -1 Корни уравнения абсциссы точек пересечения параболы с прямой

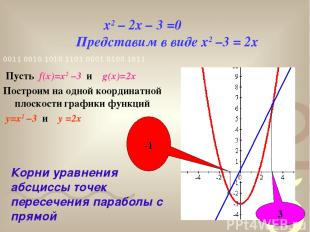
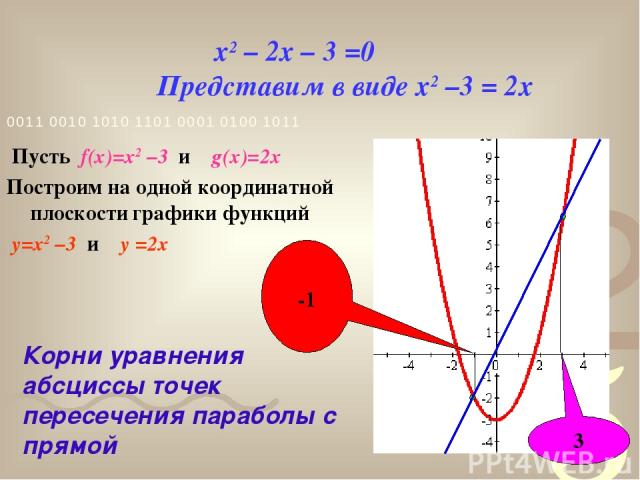
x2 – 2x – 3 =0 Представим в виде x2 –3 = 2x Пусть f(x)=x2 –3 и g(x)=2x Построим на одной координатной плоскости графики функций y=x2 –3 и y =2x -1 3 Корни уравнения абсциссы точек пересечения параболы с прямой

Графический метод решения некоторых уравнений весьма эффективен, когда нужно установить, сколько корней имеет уравнение.

Графический метод при определении количества корней уравнения 1 2 3 4 5

Неравенства Найти наименьшее натуральное решение неравенства Решить неравенства Найти область определения функции

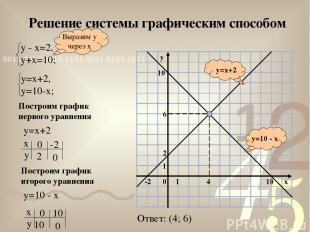
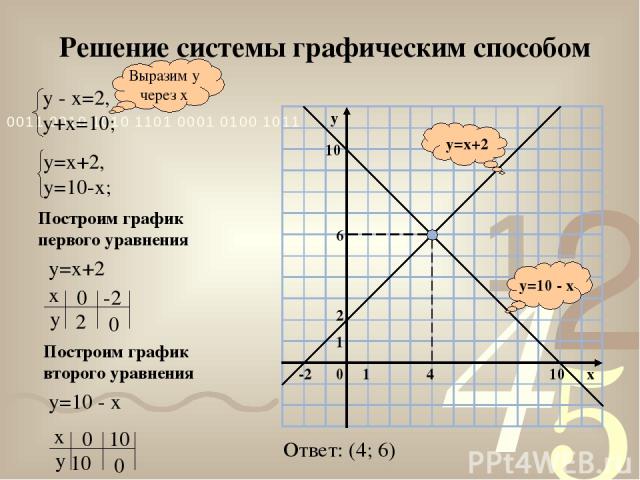
Решение системы графическим способом y=10 - x y=x+2 Выразим у через х Построим график первого уравнения у=х+2 Построим график второго уравнения у=10 - х Ответ: (4; 6)

Решение систем уравнений Найти сумму х+у, где (х;у) – решение системы Найти произведение х*у, где (х;у) – решение системы

ЕГЭ. Задания из части С. При каком значении р уравнение имеет три корня При каком значении а число корней уравнения на 2 больше а ? Найдите абсциссу точки пересечения графиков функций