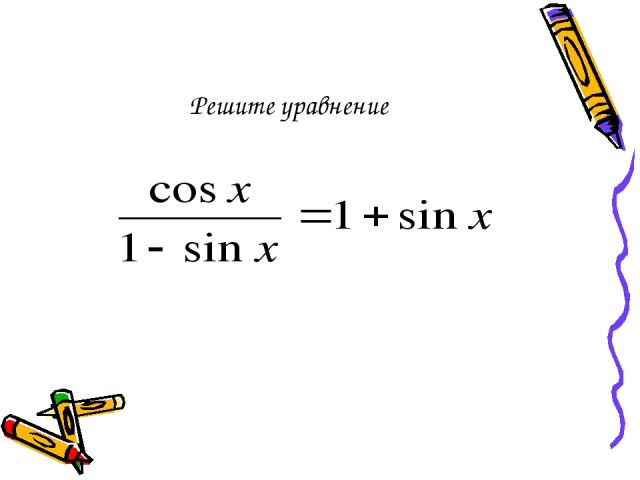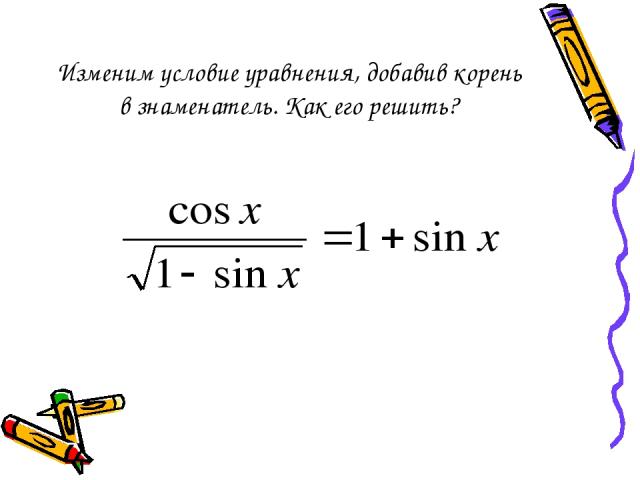Презентация на тему: Тригонометрические неравенства

Примеры простейших тригонометрических неравенств Урок по алгебре и началам анализа в 10 классе Преподавание ведется по учебнику Ш.А.Алимова учитель ГБОУ СОШ № 404 Михайловская Светлана Владимировна 5klass.net

Цели урока Сформировать умения решать тригонометрические неравенства Закрепить решение простейших тригонометрических уравнений Развивать инициативность, настойчивость, аккуратное отношение к работе

Решите уравнения устно sin x = 1 cos x = -1 tg x = 0 cos x = 2,5 sin x = 0,5 tg x = -1 cos x = 0 sin x = -1 tg x = 1 sin x =1,5 сos x = - 0,5 2tg x = - 2

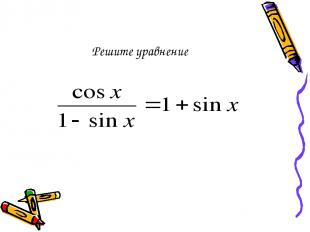
Решите уравнение

Данное уравнение равносильно системе

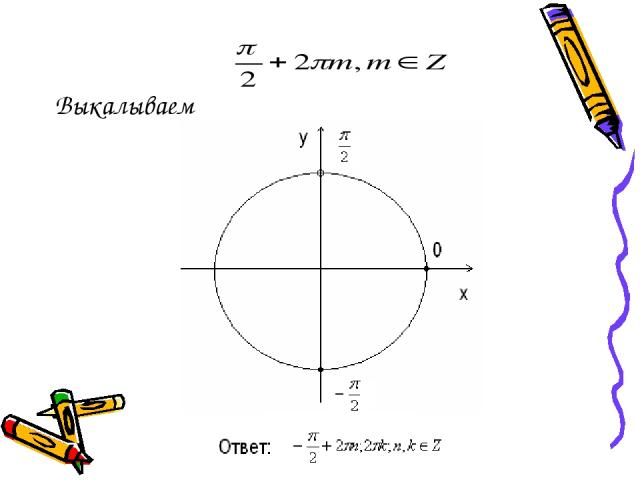
Для окончательного решения системы необходимо отобрать корни на тригонометрическом круге

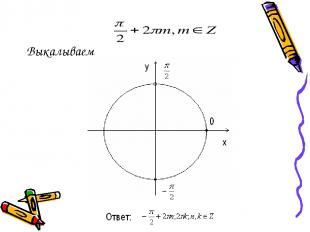
Выкалываем

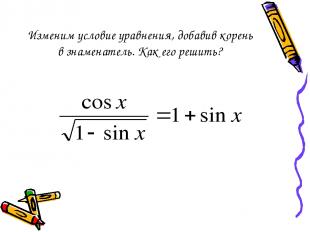
Изменим условие уравнения, добавив корень в знаменатель. Как его решить?

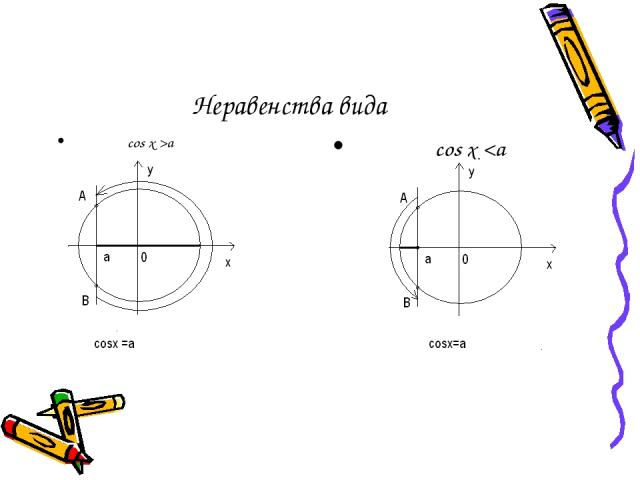
Это уравнение можно решить при условии 1-sinx >0 Для этого нам надо научиться решать тригонометрические неравенства. Определение: неравенства вида cosx >a; cosx a; sinx

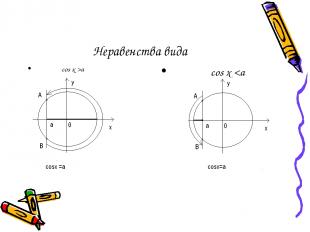
Неравенства вида cos x >a cos x

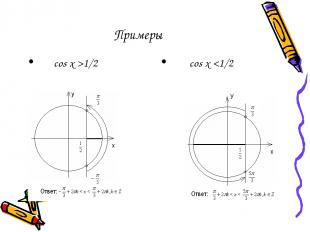
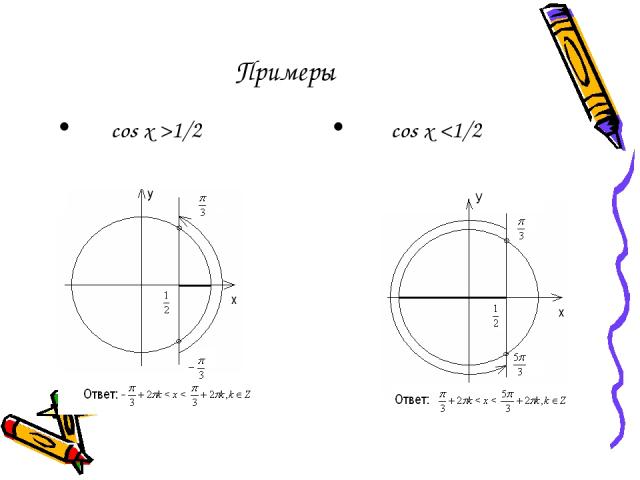
Примеры cos x >1/2 cos x

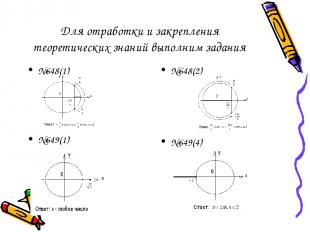
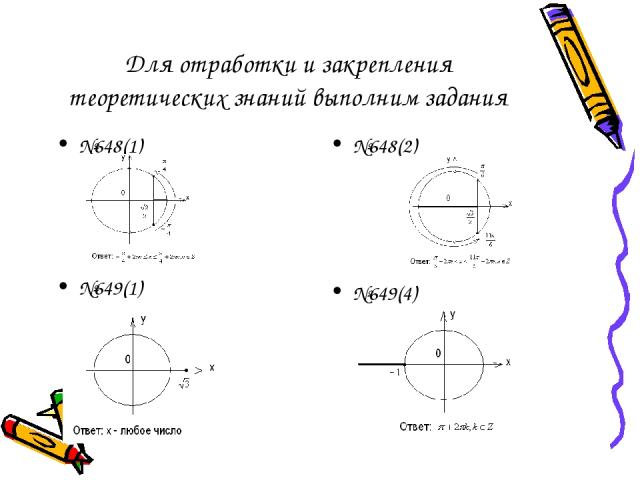
Для отработки и закрепления теоретических знаний выполним задания №648(1) №648(2) №649(1) №649(4)

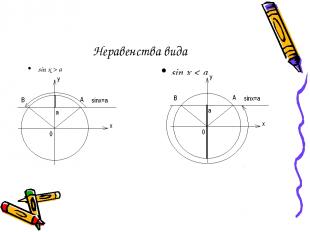
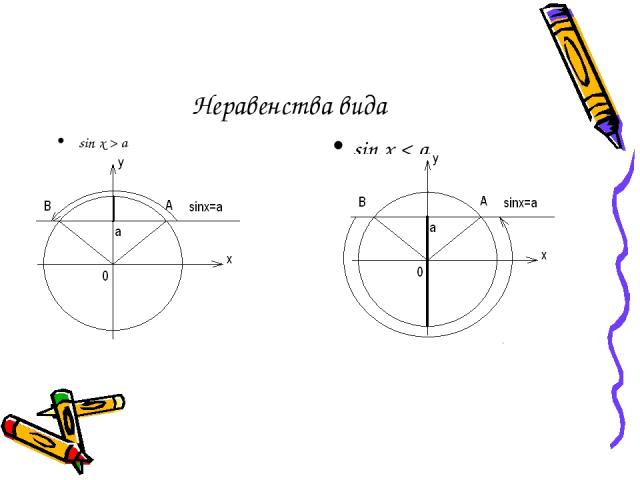
Неравенства вида sin x > a sin x < a

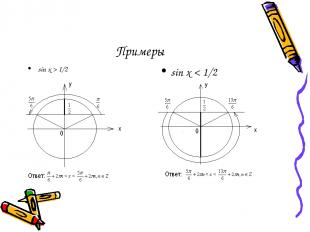
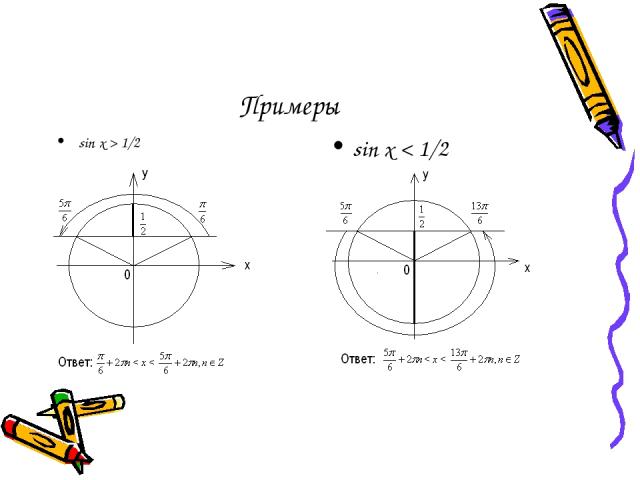
Примеры sin x > 1/2 sin x < 1/2

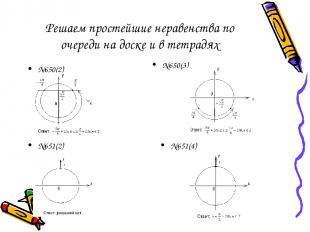
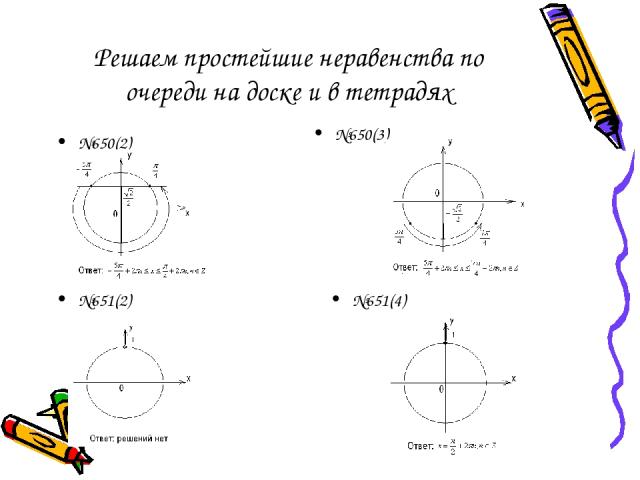
Решаем простейшие неравенства по очереди на доске и в тетрадях №650(2) №650(3) №651(2) №651(4)

Вернемся к уравнению(слайд 8) Решим неравенство, при котором определено данное уравнение 1 – sinx >0 sinx

В чем состоит алгоритм решения простейших тригонометрических неравенств? Что надо построить, чтобы решить тригонометрическое неравенство? Как построить хорду, отчего зависит ее расположение? В каком направлении подписываем значения углов, соответствующих точек пересечения хорды и окружности? В виде какого неравенства всегда записываем ответ? Может ли в ответе быть одна серия решений? В каком случае?

Домашнее задание § 37; №№ 648 (3;4); 649 (2;3);650(4)

На уроке мы рассмотрели решение тригонометрических неравенств с помощью единичной окружности. А можно решать неравенства другим способом? Подумайте над этим. Спасибо за урок!