Презентация на тему: Рекурсия

Рекурсия

Общее определение Рекурсия — метод определения класса объектов или методов предварительным заданием одного или нескольких (обычно простых) его базовых случаев или методов, а затем заданием на их основе правила построения определяемого класса. Другими словами, рекурсия — частичное определение объекта через себя, определение объекта с использованием ранее определённых. Рекурсия используется, когда можно выделить самоподобие задачи.

Рекурсия типов данных: Описание типа данных может содержать ссылку на саму себя. Подобные структуры используются при описании списков и графов. Пример описания списка : class element_of_list; // необходимо по правилам C++ class element_of_list { element_of_list *next; // ссылка на следующий // элемент того же типа int data; // некие данные // };

Рекурсия функций Рекурсия функции— это вызов функции (процедуры) из неё же самой, непосредственно (простая рекурсия) или через другие функции (сложная рекурсия), например, функция A вызывает функцию B, а функция B — функцию A. Количество вложенных вызовов функции или процедуры называется глубиной рекурсии.

Общий вид рекурсии: Если (простейший случай) тогда Решить напрямую Иначе Делать рекурсивный вызов до появления простейшего случая

Задача о вычислении Факториала Вычисление факториала – пример задачи, в которой мы можем использовать рекурсию. Факториал n Это произведение всех натуральных чисел до n включительно. К примеру: 5! = 5 * 4 * 3 * 2 * 1 = 120 4! = 4 * 3 * 2 * 1 = 24 3! = 3 * 2 * 1 = 6 2! = 2 * 1 = 2 1! = 1 0! = 1

Однако мы можем выразить факториал рекурсивно, через другие факториалы: 5! = 5 * 4! 4! = 4 * 3! 3! = 3 * 2! 2! = 2 * 1! 1! = 1 * 0! 0! = 1

Пример реализации функции на с++ int factorial(int n) { if (n == 0) { // простейший случай return 1; } else { // Рекурсивный вызов int value = factorial(n - 1); return n * value; } }

Ханойские башни: В одном из буддийских монастырей монахи уже тысячу лет занимаются перекладыванием колец. Они располагают тремя пирамидами, на которых надеты кольца разных размеров. В начальном состоянии 64 кольца были надеты на первую пирамиду и упорядочены по размеру. Монахи должны переложить все кольца с первой пирамиды на вторую, выполняя единственное условие — кольцо нельзя положить на кольцо меньшего размера. При перекладывании можно использовать все три пирамиды. Монахи перекладывают одно кольцо за одну секунду. Как только они закончат свою работу, наступит конец света.

Помочь уничтожить мир! Данная задача имеет элегантное рекурсивное решение: Итак, нам необходимо перенести n дисков со стержня (a) на стержень (c). Допустим у нас есть функция перенесения n-1 диска, тогда задача легко разрешима. Для этого вначале перенесем n-1 диск со стержня (a) на стержень (b), применяя рекурсивный вызов той же функции, затем перенесем n-ый диск со стержня (a) на стержень (c) и наконец перенесем n-1 диск со стержня (b) на стержень (c). Работа выполнена.

Функция на с++ void Step(int n, char a, char b, char c) // n - количество колец; // a, b, c - башни; { // т. к. на каждом шаге количество колец будет уменьшаться на один, // это условие будет условием выхода из рекурсии if (n <= 0) return; Step(n-1, a, c, b); printf("диск %d с %c на %c \n", n, a, b); Step(n-1, c, b, a); }

Цена рекурсии Использование рекурсии может сократить размер исходного кода программы и сделать код более элегантным и понятным. Однако рекурсия имеет и свои недостатки…

Пример: Вычисление чисел фибоначчи long fib( int n ) { if( n <= 1 ) return n; else return fib( n - 1 ) + fib( n - 2 ); }

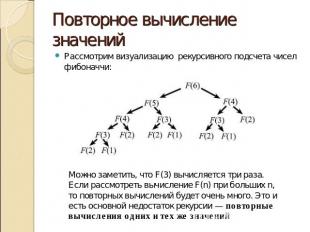
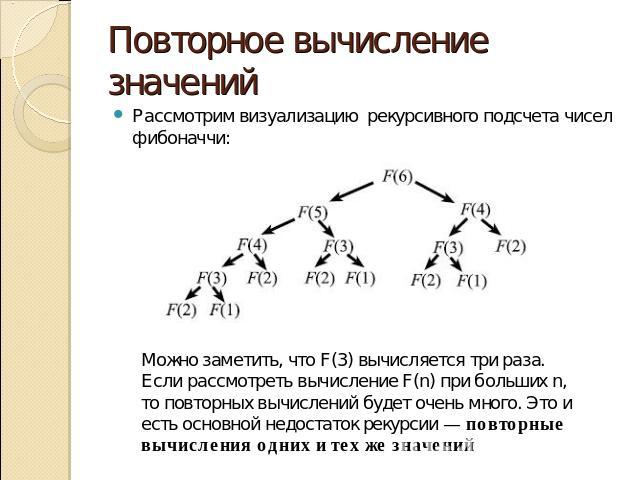
Повторное вычисление значений Рассмотрим визуализацию рекурсивного подсчета чисел фибоначчи: Можно заметить, что F(3) вычисляется три раза. Если рассмотреть вычисление F(n) при больших n, то повторных вычислений будет очень много. Это и есть основной недостаток рекурсии — повторные вычисления одних и тех же значений

Улучшения Для избавления от вычисления одних и тех же значений можно где-то хранить уже посчитанные значения, например как это сделано ниже с использованием итераций вместо рекурсии. long F(unsigned int n) { long F_1 = 1, F_2 = 0, F_cur; if(n <= 1) return n; for(unsigned int k = 2; k <= n; k++) { F_cur = F_1 + F_2; F_2 = F_1; F_1 = F_cur; } return F_cur; }

Требовательность к памяти Алгоритмы, использующие рекурсию весьма требовательны к памяти. Вернемся к примеру с рекурсивным вычислением факториала. При выполнении этого алгоритма образуется стек, в который записываются результаты работы функции на каждой итерации. Однако чем большее число мы будем вычислять, тем больше нам потребуется памяти.

Рекурсия и стек Каждый шаг рекурсии представляет собой независимый алгоритм (отдельный «экземпляр» функции). В случае ветвящейся рекурсии один такой алгоритм порождает несколько подобных, поскольку все они выполняются на одном процессоре, возникают «отложенные шаги», которые необходимо выполнить «потом». Возникает вопрос, а где, собственно, говоря, сохраняются данные об этих отложенных шагах. В случае использования обычной рекурсии само текущее состояние алгоритма, его локальные данные (например, индекс цикла перебора вариантов) и задают поведение текущего шага рекурсии «в будущем». При рекурсивном вызове это состояние запоминается в стеке, при возвращении – автоматически продолжает текущий шаг от точки «замерзания». Но то, что делается автоматически, можно реализовать в явном виде с использованием специально организованного программного стека, если помещать в него набор данных, соответствующих начальному состоянию каждого следующего шага. Тогда рекурсивный алгоритм становится простым циклическим.

Схема рекурсивного алгоритма с явным стеком stack S; // Явный стек data D0={…}; // Начальное состояние – первый шаг S.push(D0); // Поместить в стек while(S.size()!=0){ // Цикл извлечения шагов из стека data D=S.pop(); // Извлечь из стека данные нового шага … // Очередной шаг if (тупик) continue; if (успех) break; for (int i=0; i<N; i++) { data D1; D1=… // Данные нового шага S.push(D1); // сформировать и поместить в стек } }

Волновой алгоритм Рекурсивный алгоритм дает нам последовательность выполнения шагов, известную как «рекурсивный обход дерева», которая определяется свойствами стека, его реализующего. Имеется другая последовательность обхода, которую образно можно представить в виде волны, распространяющейся от корня дерева к вершинам. Такой обход уже нельзя назвать рекурсивным, потому что ее нельзя реализовать с помощью механизма явного рекурсивного вызова функции. Тем не менее, идея разветвляющегося алгоритма с идентичными шагами остается в силе. Для того, чтобы шаги алгоритма выполняются «по слоям», нужно вместо явного стека использовать аналогичную очередь шагов алгоритма.

Задача поиска минимального пути Идея «волны» иногда позволяет резко сократить число просматриваемых вариантов в сравнении с рекурсивным перебором. Например, алгоритм определения кратчайших путей на графе можно решить, представив его как распространение «волны» из исходной вершины. Такая волна, проходя через вершины, запоминает в них длину пройденного пути. Перечислим «составные части» такого алгоритма: - прохождение волны через вершину моделируется помещением ее в очередь; - волновой алгоритм извлекает вершины из очереди и помещает в нее некоторую часть «соседей», в которые эта волна распространяется; - при распространении волны в соседнюю вершину в нее помещается длина пути из начальной: она равна длине пути до текущей (которая уже содержится в текущей вершине согласно этому же алгоритму) плюс расстояние до «соседа»; - волна распространяется в непройденные волной вершины; - волна распространяется в пройденные вершины, если новое расстояние меньше старого, в этом случае она вызывает «повторную волну»; - зацикливание алгоритма и повторное прохождение волны в обратном направлении исключается предыдущим условием.

Пример реализации // Поиск кратчайших путей на графе – волновой алгоритм #define N 100 int A[N][N]; // матрица расстояний до соседей int W[N]; // матрица расстояний от начального void main(){ int nc=0,ncmp=0; for (int i=0;i<N;i++) W[i]=-1; create(0.05); int n0=0; // Начальная вершина и расстояние до самой себя =0 W[n0]=0; queue<int,100> Q; // Очередь номеров вершин Q.in(n0); // Поместить исходную в очередь while(Q.size()!=0){ // Пока очередь не пуста int ni=Q.out(); // Извлечь номер очередной вершины if (W[ni]==-1) continue; // ошибка - она еще не пройдена nc++; // подсчет трудоемкости алгоритма

Продолжение for (i=0;i<N;i++) // проверка всех соседей if (A[ni][i]!=0){ // Это неотмеченный сосед if (W[i]==-1 || W[i]>W[ni]+A[ni][i]) { //или сосед с более длинным путем W[i]=W[ni]+A[ni][i]; // Уменьшить длину пути до него Q.in(i); // Поместить в очередь (вторая волна) } ncmp++; // подсчет трудоемкости алгоритма } } for (i=0;i<N;i++) printf("%d ",W[i]); printf("\nnc=%d ncmp=%d\n",nc,ncmp); }

Резюме Таким образом, Всегда полезно подумать о замене рекурсии на циклические алгоритмы. Однако в некоторых случаях решение задачи без рекурсии может быть чрезвычайно сложным и прирост производительности не будет стоить потраченных усилий.

Если (Вы чего-то не поняли) то:Запустите презентацию сначала.Иначе:Спасибо за внимание, на этом презентация закончена!