Презентация на тему: Методы решения комбинаторных задач

Тема урока: «Решение комбинаторных задач с помощью графов» 900igr.net

Вопросы к уроку. Чем занимается комбинаторика? Что такое граф? Какие задачи относятся к комбинаторным? Как решаются комбинаторные задачи с помощью графов?

1.Чем занимается комбинаторика? Комбинаторика-раздел математики ,рассматривающий вопросы(задачи), связанные с подсчётом числа всевозможных комбинаций из элементов данного конечного множества при сделанных исходных предположениях.

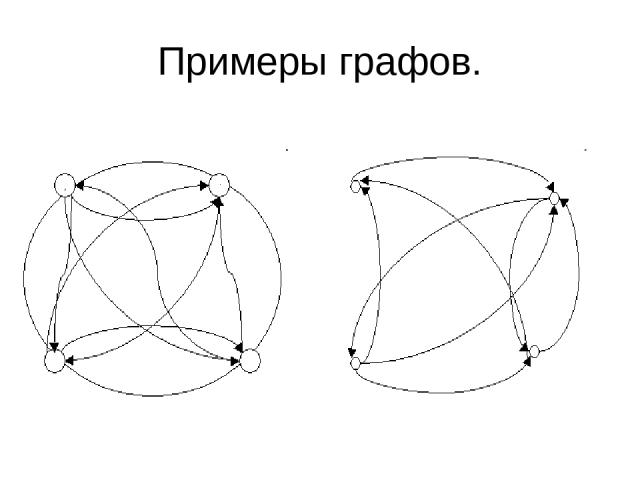
2.Что такое граф? Граф-геометрическая фигура,состоящая из точек(вершины графа) и линий,их соединяющих(рёбра графа).

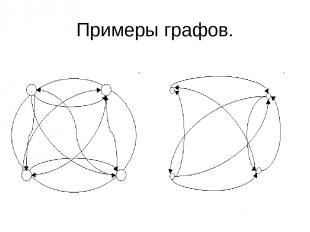
Примеры графов.

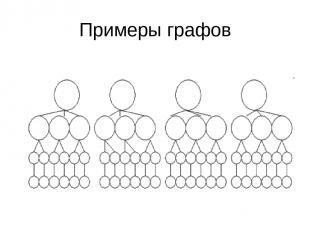
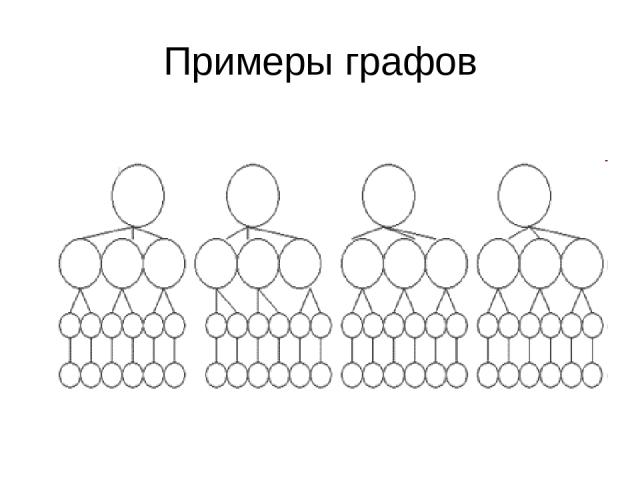
Примеры графов

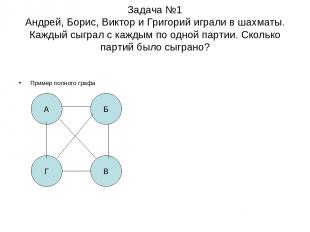
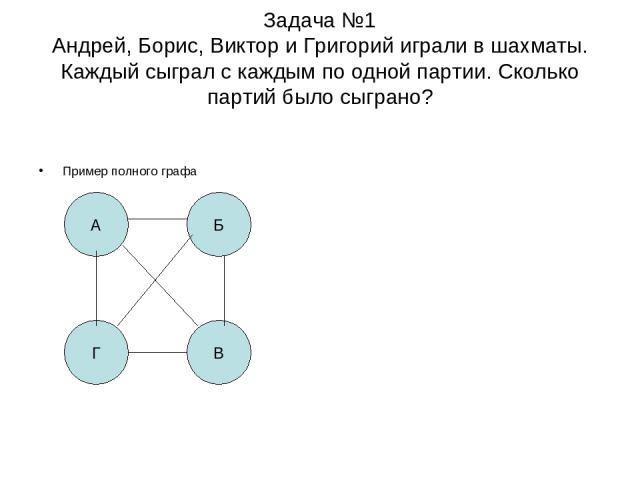
Задача №1 Андрей, Борис, Виктор и Григорий играли в шахматы. Каждый сыграл с каждым по одной партии. Сколько партий было сыграно? Пример полного графа А Б Г В

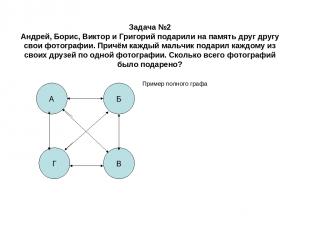
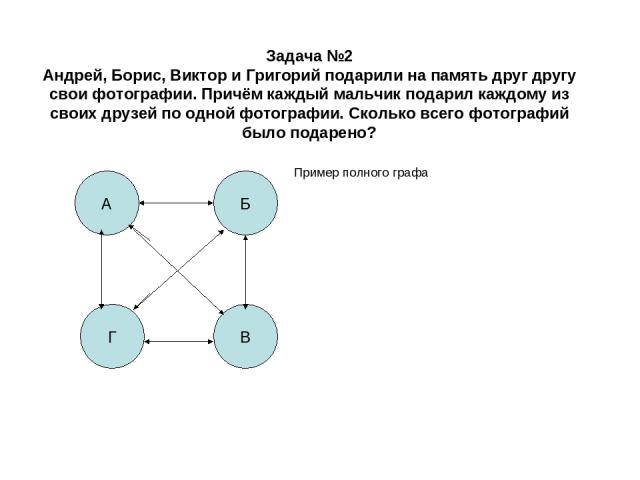
Задача №2 Андрей, Борис, Виктор и Григорий подарили на память друг другу свои фотографии. Причём каждый мальчик подарил каждому из своих друзей по одной фотографии. Сколько всего фотографий было подарено? Пример полного графа А Г Б В

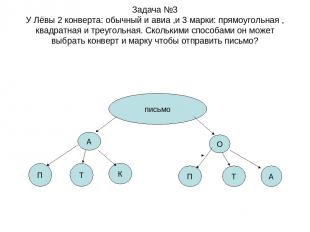
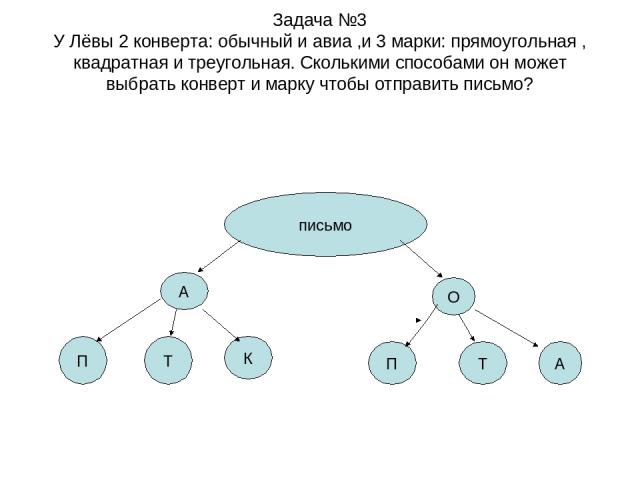
Задача №3 У Лёвы 2 конверта: обычный и авиа ,и 3 марки: прямоугольная , квадратная и треугольная. Сколькими способами он может выбрать конверт и марку чтобы отправить письмо? письмо А О П Т К П Т А

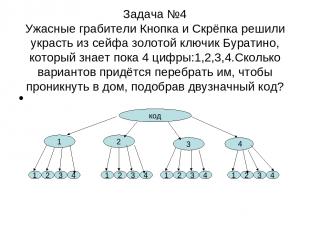
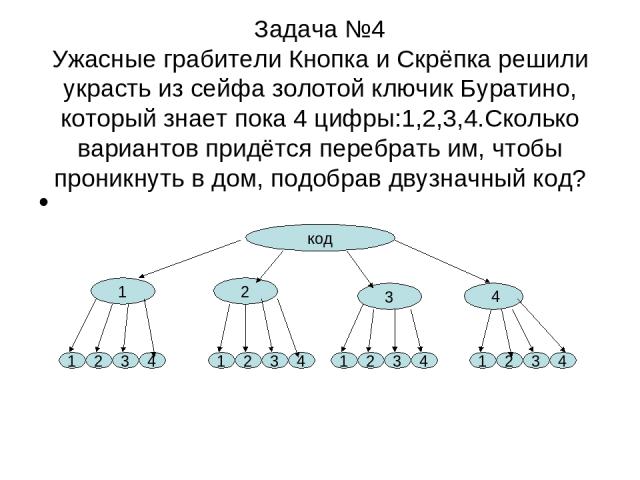
Задача №4 Ужасные грабители Кнопка и Скрёпка решили украсть из сейфа золотой ключик Буратино, который знает пока 4 цифры:1,2,3,4.Сколько вариантов придётся перебрать им, чтобы проникнуть в дом, подобрав двузначный код? код 1 2 3 1 2 4 3 1 2 3 4 1 2 3 4 1 2 3 4 4

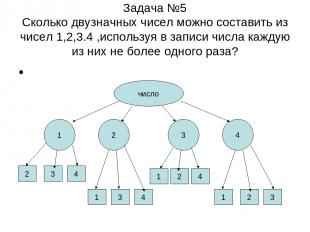
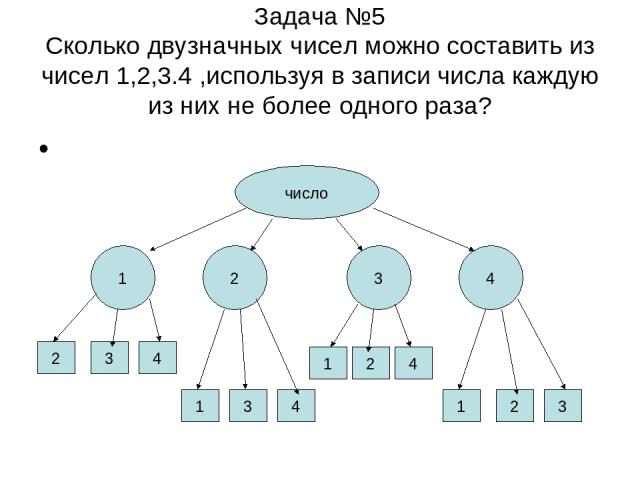
Задача №5 Сколько двузначных чисел можно составить из чисел 1,2,3.4 ,используя в записи числа каждую из них не более одного раза? число 1 2 3 4 2 3 4 1 3 4 1 2 4 1 2 3

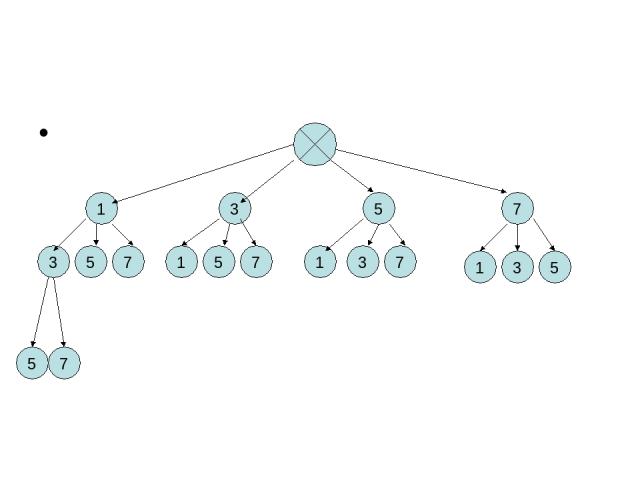
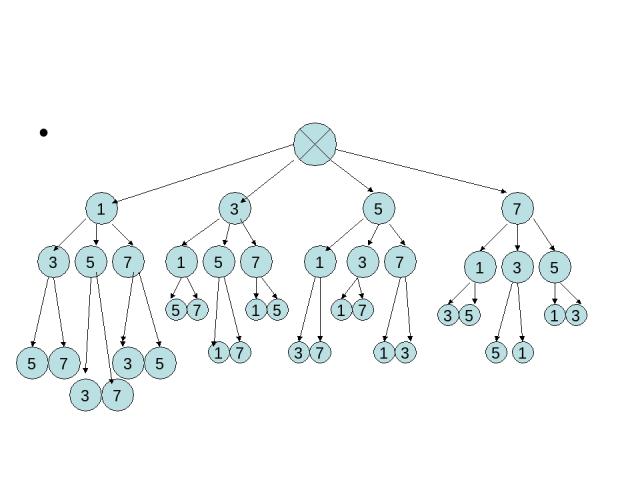
Задача № Сколько трёхзначных чисел можно составить из цифр 1,3,5,7, используя в записи числа каждую из них не более одного раза?

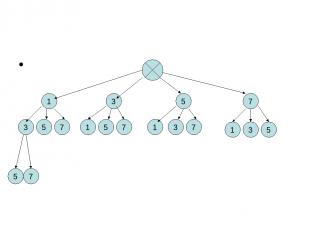
1 3 5 7 3 5 7 1 5 7 1 3 7 1 3 5 5 7

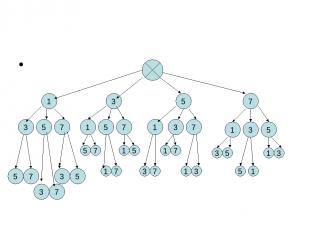
1 3 5 7 3 5 7 1 5 7 1 3 7 1 3 5 5 7 3 7 3 5 7 5 1 7 1 5 3 7 1 7 1 3 3 5 5 1 1 3

Задача № Сколько трёхзначных чисел можно записать из цифр 1,2,3 при условии ,что 1)цифры в записи числа должны быть различны;2)цифры в записи числа могут повторяться?

Задача №(устно) Сколькими способами Петя и Вова могут занять места за двухместной партой? Сколькими способами вы можете рассадить 3-х гостей на 3-х разноцветных табуретках. №. Сколькими способами вы можете рассадить 4-х гостей на 4-х разноцветных табуретках? №.Сколькими способами вы можете рассадить 5-х гостей на 5-х разноцветных табуретках?

«Правило произведения». Если существует n вариантов выбора первого элемента и для каждого из них есть m вариантов выбора второго элемента,то всего существует nxm различных пар с выбранными первым и вторым элементами.

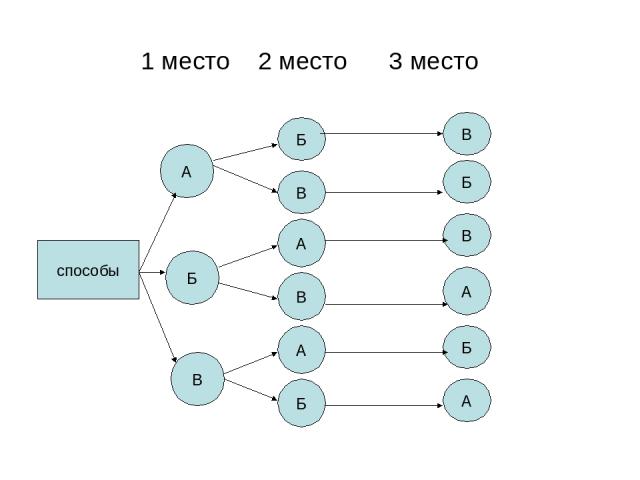
Задача № №.Антон, Борис и Василий купили 3 билета на 1-е,2-е и 3-е места первого ряда на футбольный матч. Сколькими способами они могут занять имеющиеся места?

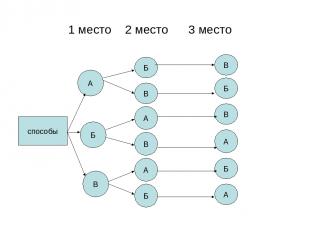
1 место 2 место 3 место способы А Б В Б В А В А Б В Б В А Б А

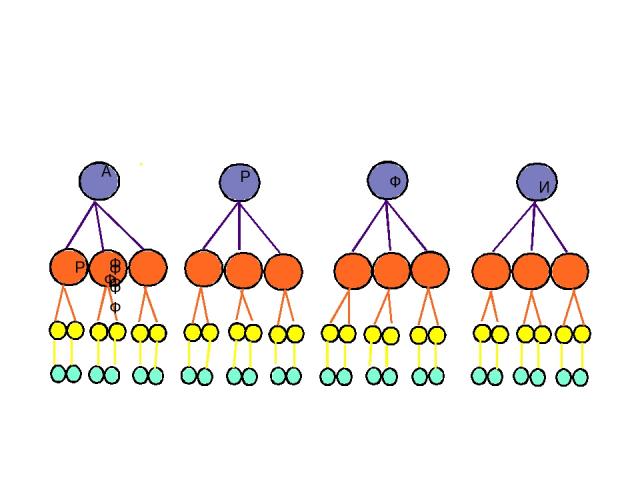
Задача № №.В пятницу у вас 4 уроков: алгебра, русский, физика, история. Сколькими способами можно составить расписание на пятницу?

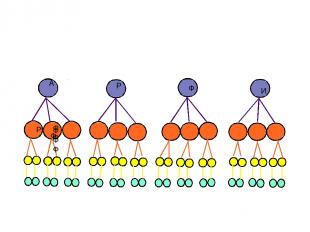
А Р Ф И Р ФФФ Ф ФФ