Презентация на тему: Математическая логика

Математическая логика Единственное средство улучшить наши умозаключения состоит в том, чтобы сделать их столь же наглядными, как и у математиков, - такими, что их ошибочность можно было бы увидеть глазами, и если между людьми возникают разногласия, достаточно было бы только сказать «Вычислим!», чтобы без дальнейших околичностей стало ясно, кто прав. Г.В.Лейбниц 900igr.net

Логика-это наука, изучающая формы и законы мышления, закономерности мыслительного процесса. Логика высказываний- раздел логики, в котором вопрос об истинности или ложности высказываний рассматривается и решается на основе изучения способа построения высказываний из элементарных с помощью логических связок.

Высказывания. Классификация высказываний. Высказыванием называется всякое утверждение (повествовательное предложение), про которое всегда определённо и объективно можно сказать, является ли оно истинным или ложным. Высказывания: 1.Абсолютно истинные 2. Абсолютно ложные логические константы Высказывания обозначаются заглавными латинскими буквами: А, В, С и т. д.

А – «Волга впадает в Каспийское море» А=1 В – «3 больше 5» В=0 Высказывания, которые нельзя разбить на еще более мелкие, называются простыми, а сконструированные при помощи логических связок – сложными.

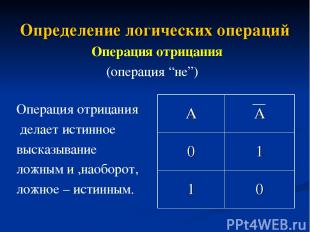
Определение логических операций Операция отрицания (операция “не”) Операция отрицания делает истинное высказывание ложным и ,наоборот, ложное – истинным. А А 0 1 1 0

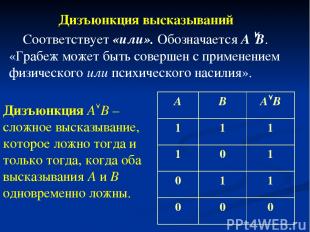
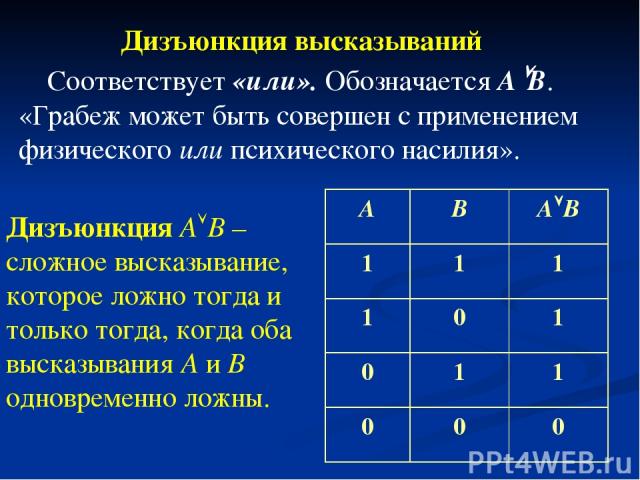
Соответствует «или». Обозначается А В. «Грабеж может быть совершен с применением физического или психического насилия». Дизъюнкция А В – сложное высказывание, которое ложно тогда и только тогда, когда оба высказывания А и В одновременно ложны. Дизъюнкция высказываний А В A B 1 1 1 1 0 1 0 1 1 0 0 0

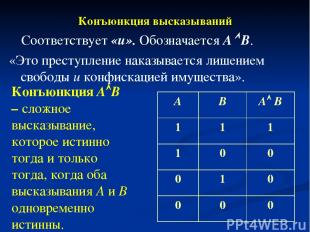
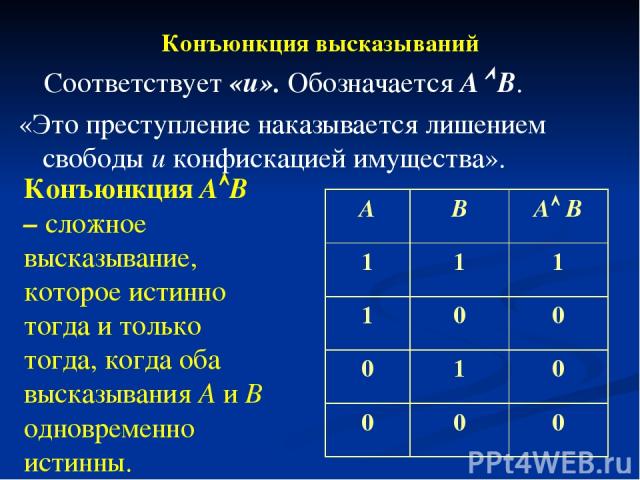
Конъюнкция высказываний Соответствует «и». Обозначается А В. «Это преступление наказывается лишением свободы и конфискацией имущества». Конъюнкция А В – сложное высказывание, которое истинно тогда и только тогда, когда оба высказывания А и В одновременно истинны. А В A B 1 1 1 1 0 0 0 1 0 0 0 0

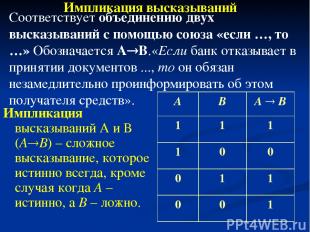
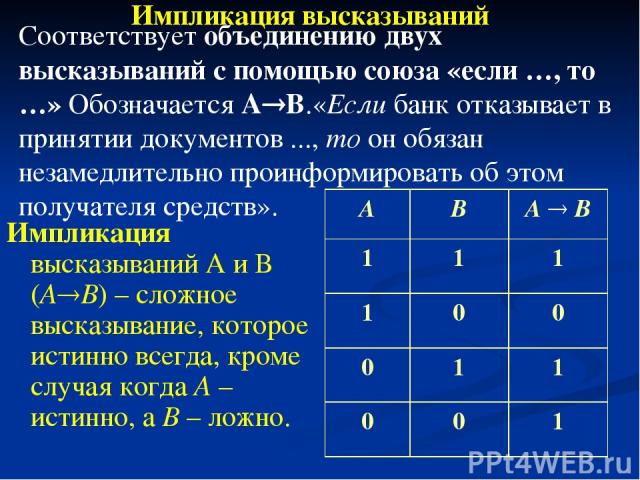
Импликация высказываний А и В (А В) – сложное высказывание, которое истинно всегда, кроме случая когда А – истинно, а В – ложно. Импликация высказываний Соответствует объединению двух высказываний с помощью союза «если …, то …» Обозначается А В.«Если банк отказывает в принятии документов ..., то он обязан незамедлительно проинформировать об этом получателя средств». А В A B 1 1 1 1 0 0 0 1 1 0 0 1

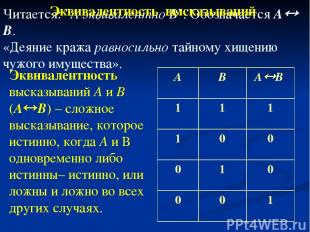
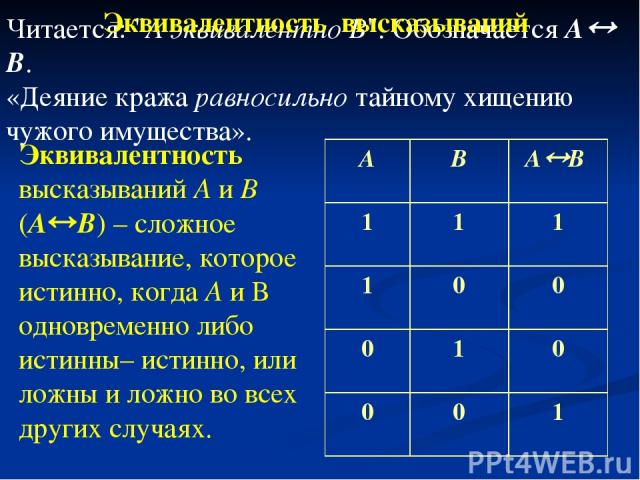
Читается: "А эквивалентно В". Обозначается А В. «Деяние кража равносильно тайному хищению чужого имущества». Эквивалентность высказываний А и В (А В) – сложное высказывание, которое истинно, когда А и В одновременно либо истинны– истинно, или ложны и ложно во всех других случаях. Эквивалентность высказываний А В А В 1 1 1 1 0 0 0 1 0 0 0 1

Моделирование логической структуры правовой нормы Логическая структура правовой нормы: N= (( J→D ) ^ ( J ^ D ))→ S , где J- условие действия нормы права; D- правовое предписание; S- санкция. Структура норм уголовного права: (P≡Q)→S P-конкретный состав преступления; Q-совокупность признаков этого состава; S-санкция, установленная за совершение определённого преступления.

Логические формулы. Таблицы истинности. A→B  C ; (A↔A B )→B ^ A и т.д. Такие высказывания называются логическими формулами или булевыми функциями , а входящие в них простые высказывания- логическими переменными. Символы ¬ ‚ ^ , , → , ↔ называют логическими связками.

Таблица истинности - перебор всех возможных комбинаций значений простых высказываний, из которых состоит сложное, и указание соответствующих значений сложного высказывания.

Равносильные логические формулы. Две логические формулы называются равносильными, если при любых значениях входящих в них логических переменных эти формулы принимают одинаковые значения. Равносильность формул обозначается с помощью знака ≡ : A↔B≡(A→B)^(B→A).

Понятие тавтологии. Законы логики. Если формула принимает значение «истина», то есть 1, при любых значениях входящих в неё логических переменных, то такая логическая формула называется тождественно истинная или тавтология. Факт, что высказывание А является тавтологией, обозначается так |=А. Сложное высказывание называется тождественно ложным, если оно принимает значение «ложь» при любых значениях входящих в него простых высказываний. То есть, если |=А, то А -тождественно ложно.

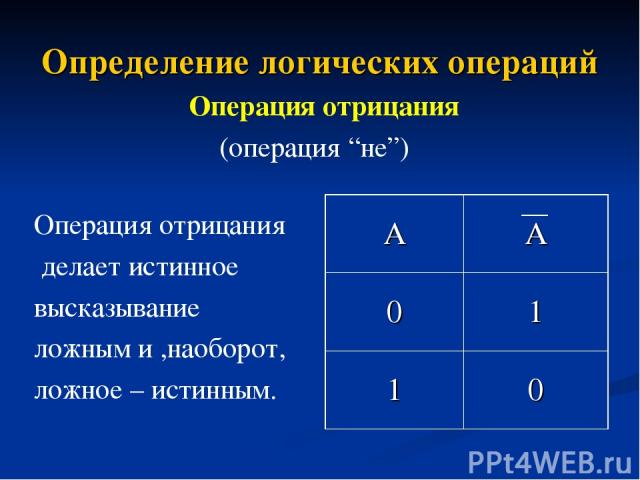
1.Закон силлогизма |=[(A→B)^(B→C)]→(A→C). Если из высказывания А следует В , а из высказывания В следует С, то можно заключить, что из А следует С. 2.Modus ponens. |=[A^(A→B)]→B. Если А – истинно и из А следует В, то В также будет истинно. 3. Закон контрапозиции. |=(A→B)↔(B→A). Следование из высказывания А высказывания В равносильно тому, что из не В следует не А.

4.Закон исключения третьего. |=A A. Для любого высказывания А или само высказывание А истинно, или его отрицание. 5.Закон противоречия. |=А^A. Для любого высказывания А неверно, что одновременно истинны и само А, и его отрицание (не А). 6.Закон двойного отрицания. |=А ↔ A. Отрицание от отрицания равносильно самому высказыванию.