Презентация на тему: Математическая логика. Основные понятия

ОСНОВНЫЕ ПОНЯТИЯ Автор: Аликина Оксана Николаевна, учитель информатики МБОУ «СОШ №77 с углубленным изучением английского языка» г. Пермь

Логика — наука о законах и правилах мышления. Формальная логика — наука о законах и формах мышления. Математическая логика - область знания в которой формальная логика изучается математическими методами.

4 в. до н.э. древнегреческий ученый Аристотель заложил основы формальной логики; 17 в. немецкий математик Лейбниц – заложил основы математической логики; 18 в. английский математик и логик Джордж Буль развил и сформулировал логические исчисления (поэтому иногда математическую логику называют Булевой алгеброй); 19 в. Готлоб Фреге, Чарльз Пирс, Бертран Рассел и др. В ПЕРВОЙ ПОЛОВИНЕ 20 в. МАТЕМАТИЧЕСКАЯ ЛОГИКА ПЕРЕШЛА В САМОСТОЯТЕЛЬНУЮ ДИСЦИПЛИНУ

1. 2. 3.

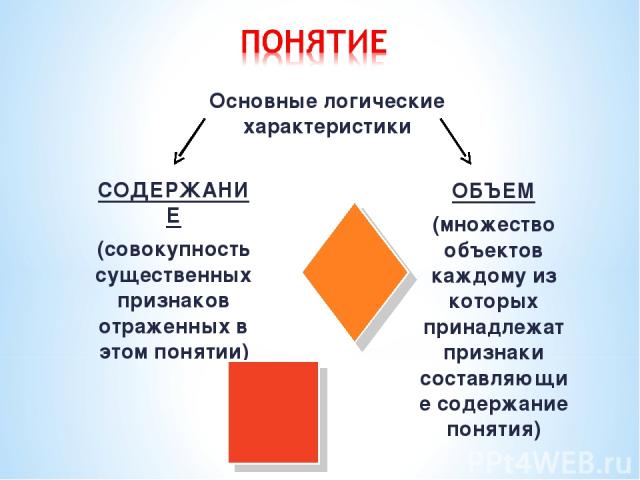
- это форма мышления, которая выделяет существенные признаки предмета или класса предметов, отличающие его от других.

Основные логические характеристики СОДЕРЖАНИЕ (совокупность существенных признаков отраженных в этом понятии) ОБЪЕМ (множество объектов каждому из которых принадлежат признаки составляющие содержание понятия)

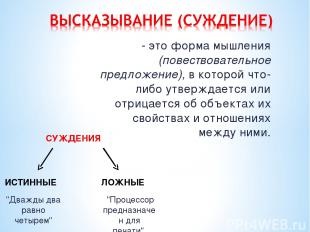
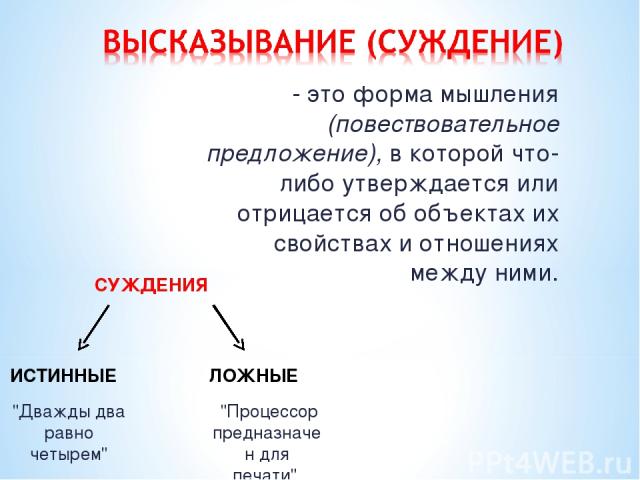
СУЖДЕНИЯ - это форма мышления (повествовательное предложение), в которой что-либо утверждается или отрицается об объектах их свойствах и отношениях между ними. ИСТИННЫЕ ЛОЖНЫЕ "Дважды два равно четырем"  "Процессор предназначен для печати" 

- это прием мышления, позволяющий на основе одного или нескольких суждений-посылок получить новое суждение (знание или вывод). Посылками умозаключения по правилам формальной логики могут быть только истинные суждения. Тогда и умозаключение будет истинным. Иначе можно прийти к ложному умозаключению. 1) Все граждане России имеют право на отдых. (истина) 2) Если цветы поливают, то они не засохнут. (истина)

Алгебра логики — это математический аппарат, с помощью которого записывается, вычисляется, упрощается и преобразуется логическое высказывание. Основным понятием математической логики является высказывание. Высказывание — это повествовательное предложение, про которое всегда можно сказать истинное оно или ложное. Истинна — 1 Ложь — 0

Высказывания обозначаются заглавными буквами латинского алфавита (простые): A,B,C,D… ВЫСКАЗЫВАНИЯ ПРОСТЫЕ СЛОЖНЫЕ «Идет дождь« А  «Если на улице дождь, то асфальт мокрый"  «На улице дождь» - А «Асфальт мокрый» - В А В

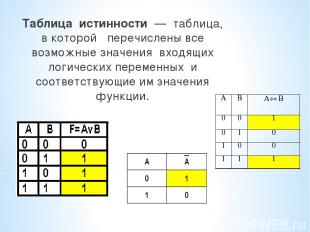
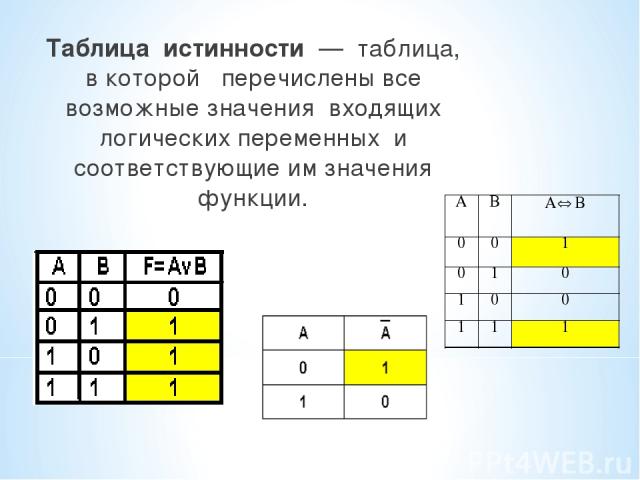
Таблица  истинности  —  таблица, в которой   перечислены все возможные значения  входящих логических переменных  и соответствующие им значения функции.

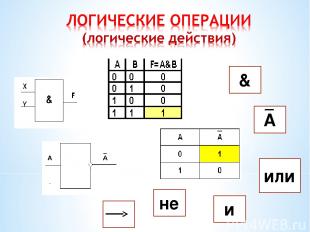
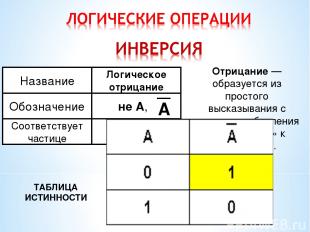
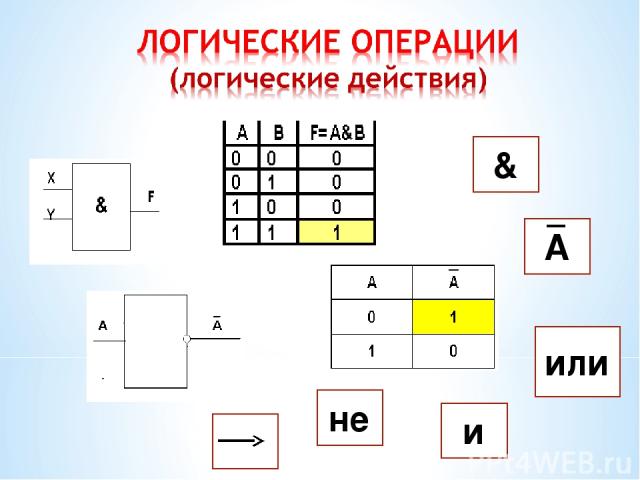
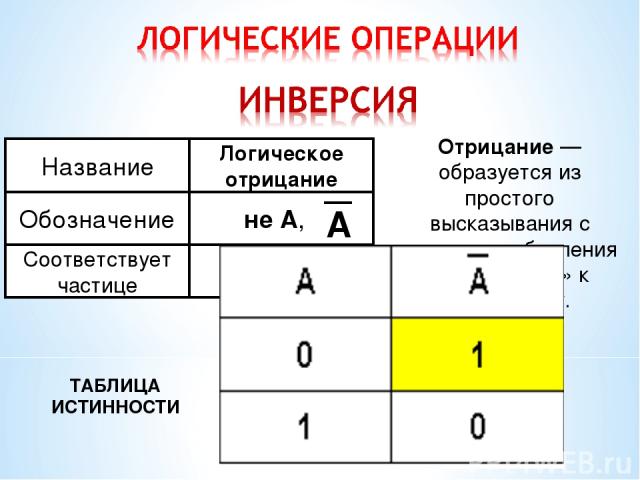
A ТАБЛИЦА ИСТИННОСТИ Отрицание — образуется из простого высказывания с помощью добавления частицы «НЕ» к сказуемому.

Сформулируйте отрицание следующим высказываниям:

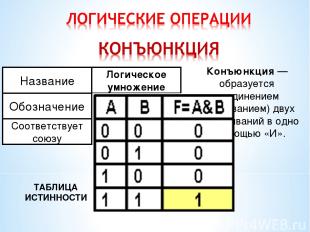
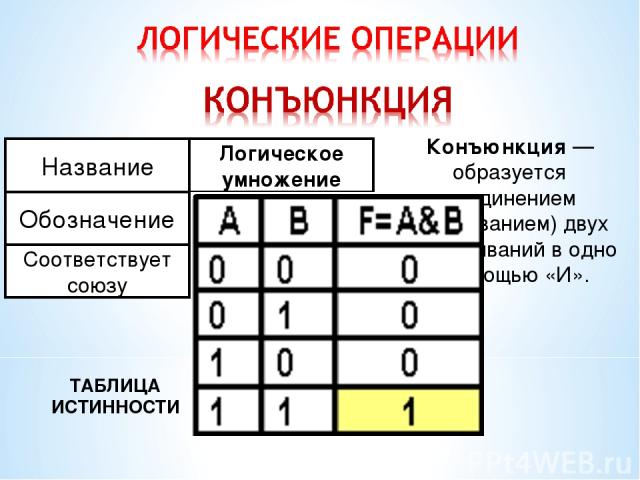
ТАБЛИЦА ИСТИННОСТИ Конъюнкция — образуется соединением (связыванием) двух высказываний в одно с помощью «И».

Определите значения истинности следующим высказываниям: А = 3*3=9 А = Санкт-Петербург расположен на Ниве В = 2+3=5 А =1 В =1 КОНЪЮНКЦИЯ = ИСТИНА (1) В = 4+7=10 А =1 В =0 КОНЪЮНКЦИЯ = ЛОЖЬ (0)

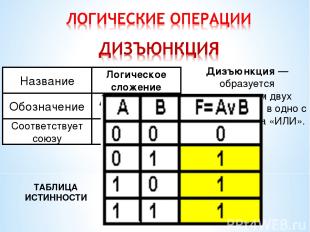
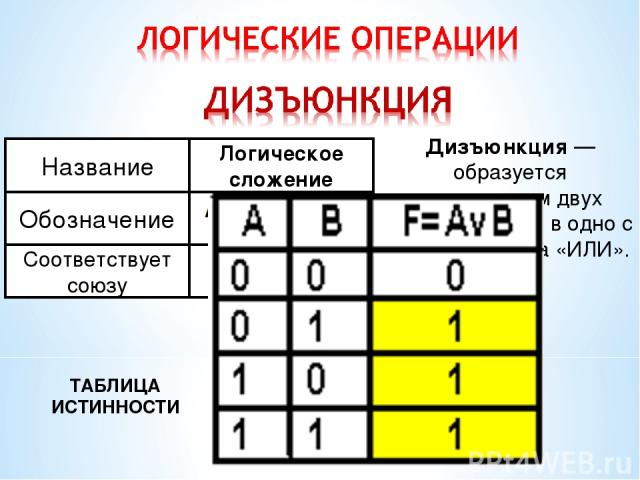
ТАБЛИЦА ИСТИННОСТИ Дизъюнкция — образуется соединением двух высказыванием в одно с помощью союза «ИЛИ».

Определите значения истинности следующим высказываниям: А = 2*2=5 А = число 2 - четное В = число 2 -простое А =1 В =1 ДИЗЪЮНКЦИЯ = ИСТИНА (1) В = белые медведи живут в Африке А =0 В =0 ДИЗЪЮНКЦИЯ = ЛОЖЬ (0)

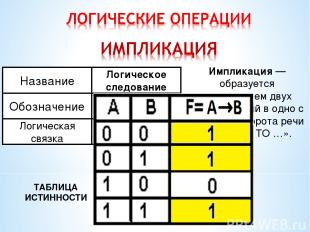
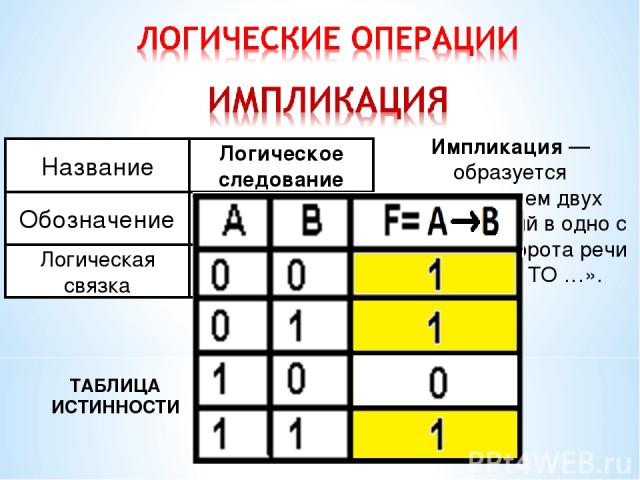
ТАБЛИЦА ИСТИННОСТИ Импликация — образуется соединением двух высказываний в одно с помощью оборота речи «ЕСЛИ …, ТО …».

Определите значение истинности следующему высказыванию: А = на улице снегопад В = замело дороги А =1 В =1 ИМПЛИКАЦИЯ = ИСТИНА (1)

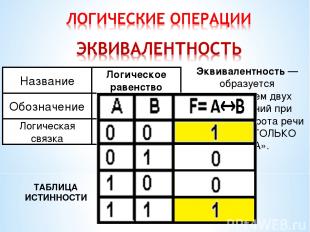
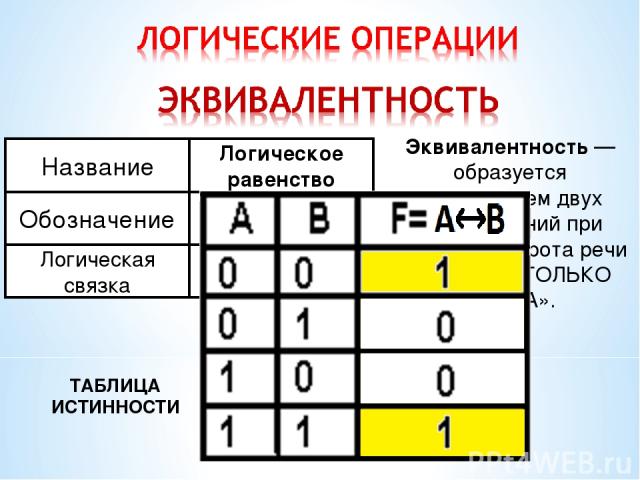
ТАБЛИЦА ИСТИННОСТИ Эквивалентность — образуется соединением двух высказываний при помощью оборота речи «ТОГДА И ТОЛЬКО ТОГДА».

Определите значение истинности следующему высказыванию: А = 12 : 6 В = 15 : 3 А =1 В =1 ЭКВИВАЛЕНТНОСТЬ = ИСТИНА (1)

Составьте и запишите по 2-3 примера на каждую логическую операцию, а так же не забудьте представить свои высказывания на языке алгебры логики.