Презентация на тему: Квадратный трёхчлен

Квадратный трёхчлен Квадратные уравнения Определение квадратного трёхчлена Корни квадратного трёхчлена

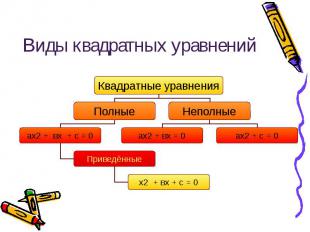
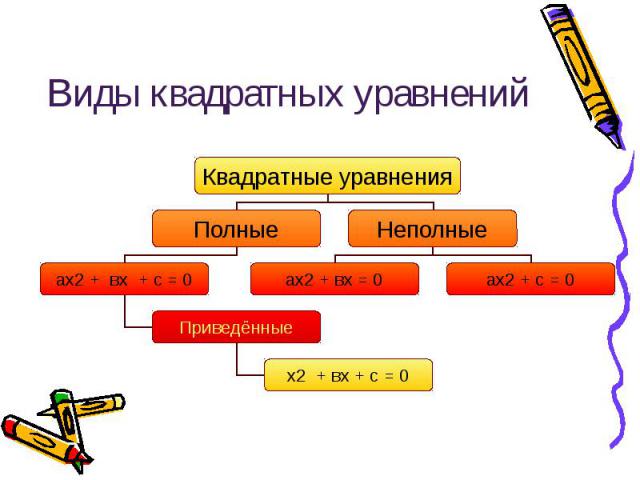
Виды квадратных уравнений

Решить эти уравнения х2 – 3х = 0 5х – 10х2 = 0 3х2 – 27 = 0 1/2х2 = 9 7х2 + 14 = 0 х2 + 5х + 6 = 0 х2 – 11х + 30 = 0 7х – 4х2 – 3 = 0 11х2 + 9х – 2 = 0 10х2 – 7х – 3 = 0

Квадратный трёхчлен ОПРЕДЕЛЕНИЕ Многочлен вида ах2 + вх + с, где х переменная, а, в, с – некоторые числа, при а≠0, называется квадратным трёхчленом Примеры: 3х2 – 5х + 1 4х2 + х (4х2 + х + 0) 7х2 – 8 (7х2 – 0х – 8)

Значение квадратного трёхчлена Значение квадратного трёхчлена неоднозначно, оно зависит от значения переменной. 5х2 – 9х + 4 х = 0; 5·02 - 9·0 + 4 = = 4 х = 1; 5·12 - 9·1 + 4 = = 0 х = 2; 5·22 - 9·2 + 4 = = 6 х = 0,8; 5·0,82 - 9·0,8 + 4 = = 0

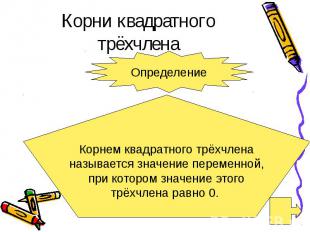
Корни квадратного трёхчлена

Вывод Для того, чтобы найти корни квадратного трёхчлена ах2 + вх + с, надо решить квадратное уравнение ах2 + вх + с = 0. Если квадратное уравнение не имеет корней, то и квадратный трёхчлен не имеет корней.

Полные квадратные уравнения ах2 + вх + с Д = в2 – 4ас ; х1,2 = (-в ± √Д)/2а Если в – чётное число, то Д = (в/2)2 – ас ; х1,2 = (-в/2 ± √Д)/а Если а + в + с = 0, то х1 = 1 ; х2 = с/а Если а – в + с = 0, то х1 = -1;х2=-с/а

Неполные квадратные уравнения ах2 + вх = 0 х(ах + в) = 0 х = 0 или ах + в =0 х = -в/а Ответ: х1=0;х2=-в/а

Приведённые квадратные уравнения х2 + вх + с = 0 Удобно решать по теореме, обратной теореме Виета: если х1 + х2 = -в х1 · х2 = с , то х1 и х2 - корни квадратного уравнения

Из истории Франсуа Виет(1540-1603) французский математик, ввёл систему алгебраических символов. Он был одним из первых, кто стал обозначать числа буквами. Формулы, выражающие зависимость корней уравнения от его коэффициентов, были введены Виетом в 1591 году.