Презентация на тему: Интегрирование рациональных функций

Интегрирование рациональных функций Дробно – рациональная функция Простейшие рациональные дроби Разложение рациональной дроби на простейшие дроби Интегрирование простейших дробей Общее правило интегрирования рациональных дробей 900igr.net

Дробно – рациональная функция Дробно – рациональной функцией называется функция, равная отношению двух многочленов: Рациональная дробь называется правильной, если степень числителя меньше степени знаменателя, то есть m < n , в противном случае дробь называется неправильной. Всякую неправильную рациональную дробь можно, путем деления числителя на знаменатель, представить в виде суммы многочлена L(x) и правильной рациональной дроби:
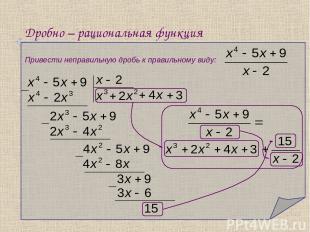
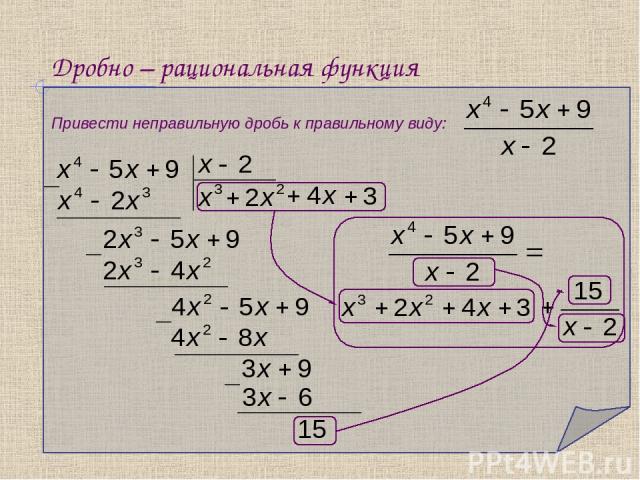
Дробно – рациональная функция Привести неправильную дробь к правильному виду:

Простейшие рациональные дроби Правильные рациональные дроби вида: Называются простейшими рациональными дробями типов.

Разложение рациональной дроби на простейшие дроби Теорема: Всякую правильную рациональную дробь , знаменатель которой разложен на множители: можно представить, притом единственным образом в виде суммы простейших дробей:

Разложение рациональной дроби на простейшие дроби Поясним формулировку теоремы на следующих примерах: Для нахождения неопределенных коэффициентов A, B, C, D… применяют два метода: метод сравнивания коэффициентов и метод частных значений переменной. Первый метод рассмотрим на примере.

Разложение рациональной дроби на простейшие дроби Представить дробь в виде суммы простейших дробей:

Интегрирование простейших дробей Найдем интегралы от простейших рациональных дробей: Интегрирование дроби 3 типа рассмотрим на примере.

Интегрирование простейших дробей

Интегрирование простейших дробей Интеграл данного типа с помощью подстановки: приводится к сумме двух интегралов: Первый интеграл вычисляется методом внесения t под знак дифференциала. Второй интеграл вычисляется с помощью рекуррентной формулы:

Интегрирование простейших дробей a = 1; k = 3

Общее правило интегрирования рациональных дробей Если дробь неправильная, то представить ее в виде суммы многочлена и правильной дроби. Разложив знаменатель правильной рациональной дроби на множители, представить ее в виде суммы простейших дробей с неопределенными коэффициентами Найти неопределенные коэффициенты методом сравнения коэффициентов или методом частных значений переменной. Проинтегрировать многочлен и полученную сумму простейших дробей.

Пример Приведем дробь к правильному виду.

Пример

Пример