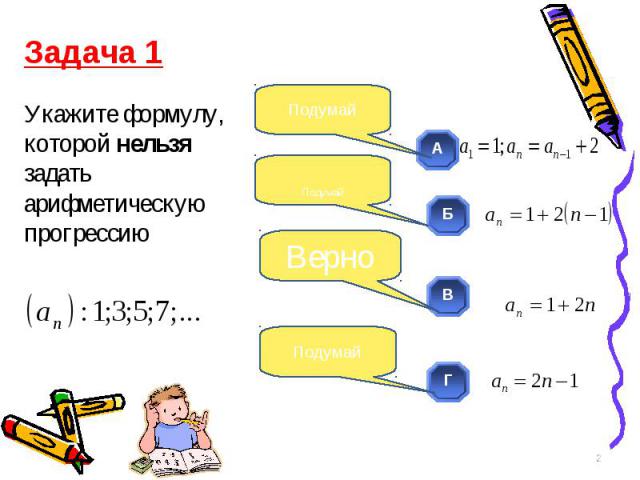
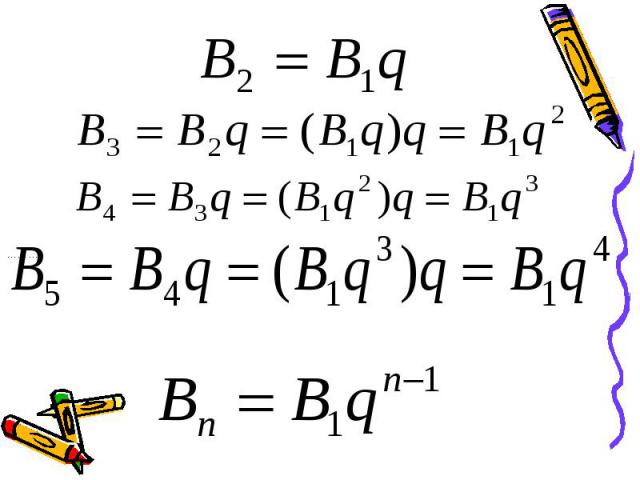Презентация на тему: Геометрические прогрессии

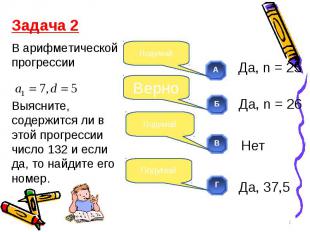
Рассмотрим последовательности: Рассмотрим последовательности: а) 2; 4; 8; 16; 32; 64; … б) 2; 6; 18; 54; 162… в)-10; 100; -1000; 10000; -100000…..

а) а) Каждый последующий член последовательности равен предыдущему члену, умноженному на 2.

б) б) -Каждый последующий член последовательности равен предыдущему члену, умноженному на 3

в) -Каждый последующий член последовательности равен предыдущему члену, умноженному на -10.

Определение. Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число. Определение. Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число. Иначе, последовательность (вn)- геометрическая прогрессия, если для любого натурального n выполняется условие и , где

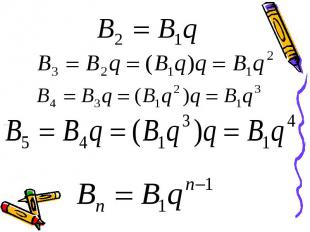
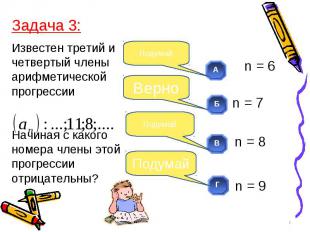
Задача 4. Задача 4. Выберите из последовательностей геометрические прогрессии. А) 3; 6; 9; 12… Б) 5; 5; 5; … В) 1;2;4;8;16; Г) -2; 2; -2; 2…

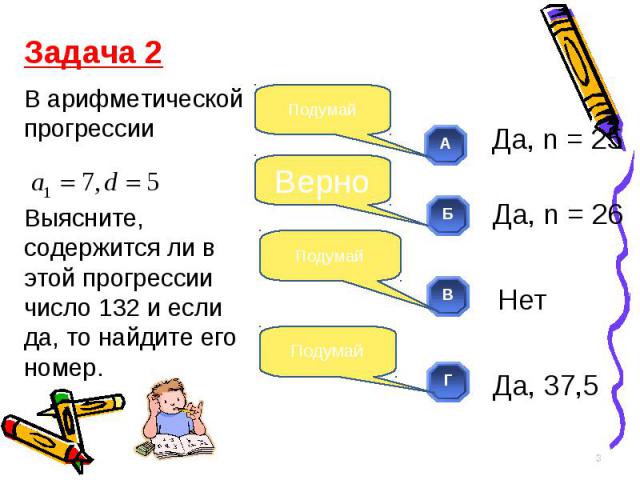
Задача 5. Задача 5. В геометрической прогрессии = 13, 4 и q=0,2. Найти Решение. По формуле n-ого члена геометрической прогрессии

Задача 6. Задача 6. Найти пятый член геометрической прогрессии: 2; -6… Решение. Зная первый и второй члены геометрической прогрессии, можно найти её знаменатель. q= -6:2= -3. Таким образом

1) Определите, какая последовательность является геометрической прогрессией 1) Определите, какая последовательность является геометрической прогрессией 2; 5; 8; 11 … . 2; 1; 0,5; 0,25 -2; -8; -32; -128 … -2; -4; -6; -8; …