Презентация на тему: Арифметический квадратный корень и его свойства

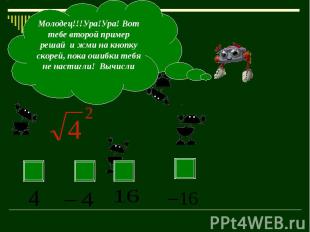
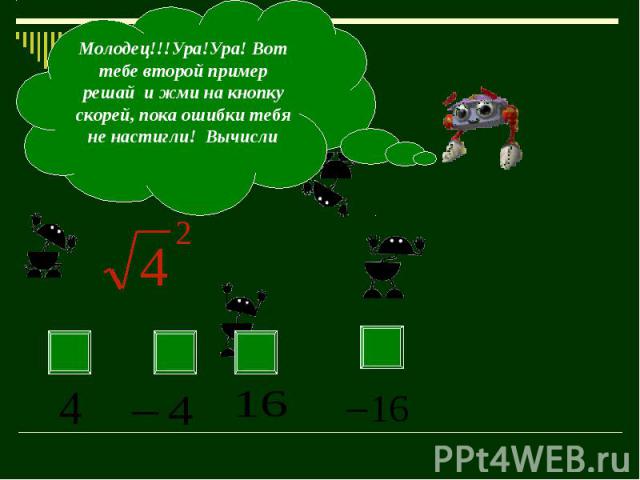
Пусть а и b – любые неотрицательные числа, с – положительное число, тогда справедливы равенства Пусть а и b – любые неотрицательные числа, с – положительное число, тогда справедливы равенства √аb = √а √b, (1) √а/с = √а /√с. (2) Для любого действительного числа а верно равенство √а2 =lаl (3)

Корень из произведения неотрицательных чисел равен произведению корней этих чисел Корень из произведения неотрицательных чисел равен произведению корней этих чисел Корень из частного от деления неотрицательного числа наположительное равен частному корней этих чисел

Равенства (1), (2), (3) помогают упрощать числовые выражения, содержащие квадратные корни Равенства (1), (2), (3) помогают упрощать числовые выражения, содержащие квадратные корни Пример 1. √80 = √16 · 5 = √16 √5 =4 √5 Пример 2. √27/25 = √9·3/25 = √9/25·√3/1=3/5· √3 Пример 3. √8 · √32 = √8·32 = √162 = 16

Преобразование √16 · 5 = √16 √5 =4 √5 Преобразование √16 · 5 = √16 √5 =4 √5 Называют вынесением множителя из-под знака корня Обратное преобразование 4 √5 = √16 · 5 называют внесением множителя под знак корня Преобразование

П.3.5 П.3.5 №151(е - ж)