Презентация на тему: Вычисление площади криволинейной трапеции


1 задание 1 задание
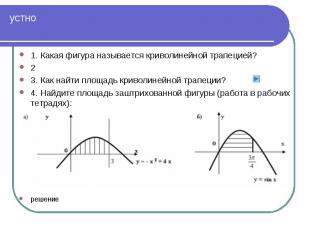
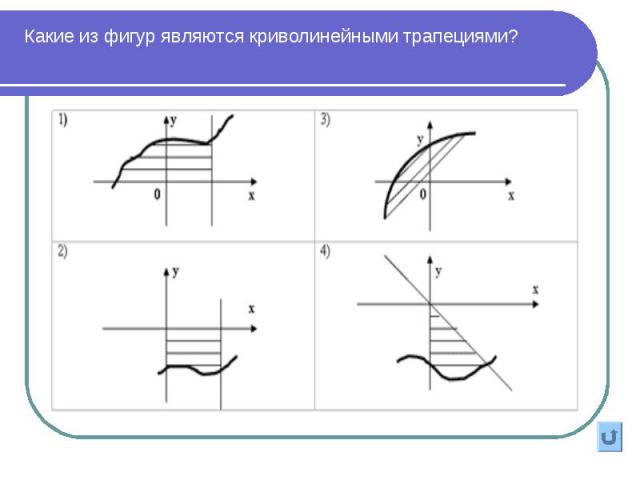
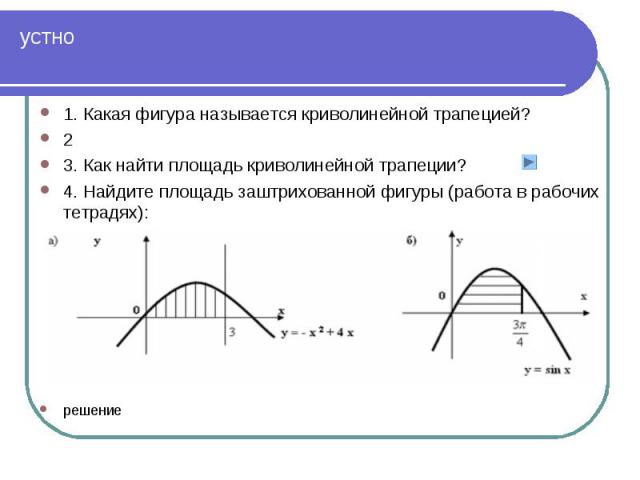
1. Какая фигура называется криволинейной трапецией? 1. Какая фигура называется криволинейной трапецией? 2 3. Как найти площадь криволинейной трапеции? 4. Найдите площадь заштрихованной фигуры (работа в рабочих тетрадях): решение
![Фигура, ограниченная снизу отрезком [a;b] оси Ох, сверху графиком непрерывной фу Фигура, ограниченная снизу отрезком [a;b] оси Ох, сверху графиком непрерывной фу](https://fs1.ppt4web.ru/images/95232/129669/310/img3.jpg)
Фигура, ограниченная снизу отрезком [a;b] оси Ох, сверху графиком непрерывной функции у = f(x), принимающей положительные значения, а с боков отрезками прямых х = а и х = b, называется криволинейной трапецией. Фигура, ограниченная снизу отрезком [a;b] оси Ох, сверху графиком непрерывной функции у = f(x), принимающей положительные значения, а с боков отрезками прямых х = а и х = b, называется криволинейной трапецией. Формула для вычисления площади криволинейной трапеции S = F(a) – F(b) = формула Ньютона – Лейбница
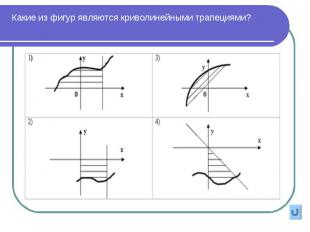

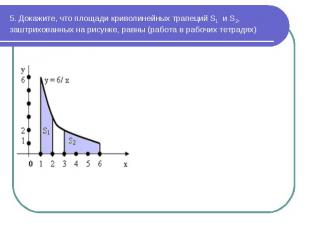
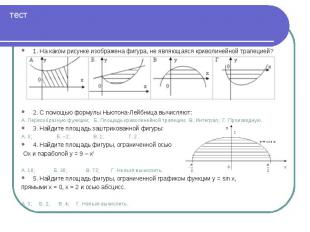
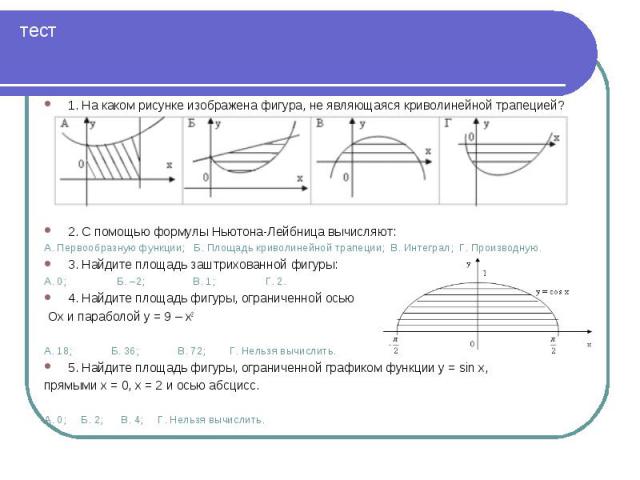
1. На каком рисунке изображена фигура, не являющаяся криволинейной трапецией? 1. На каком рисунке изображена фигура, не являющаяся криволинейной трапецией? 2. С помощью формулы Ньютона-Лейбница вычисляют: А. Первообразную функции; Б. Площадь криволинейной трапеции; В. Интеграл; Г. Производную. 3. Найдите площадь заштрихованной фигуры: А. 0; Б. –2; В. 1; Г. 2. 4. Найдите площадь фигуры, ограниченной осью Ох и параболой у = 9 – х2 А. 18; Б. 36; В. 72; Г. Нельзя вычислить. 5. Найдите площадь фигуры, ограниченной графиком функции у = sin x, прямыми х = 0, х = 2 и осью абсцисс. А. 0; Б. 2; В. 4; Г. Нельзя вычислить.

1. Б; Г 1. Б; Г 2. Б,В; 3. Г; 4. Б; 5. В.

1. При каких значениях а площадь фигуры, ограниченной линиями у = х2, у = 0, х = а, равна 9? 1. При каких значениях а площадь фигуры, ограниченной линиями у = х2, у = 0, х = а, равна 9?

Площадь криволинейной трапеции вычисляется с помощью интеграла. Интеграл вычисляется с помощью формулы Ньютона-Лейбница (если удается найти первообразную) или с помощью интегральных сумм (если не удается найти первообразную). Площадь криволинейной трапеции вычисляется с помощью интеграла. Интеграл вычисляется с помощью формулы Ньютона-Лейбница (если удается найти первообразную) или с помощью интегральных сумм (если не удается найти первообразную). Дома прочитать §58, в тексте параграфа задачи 3, 4. Дома выполнить № 1014 (2,4), 1009 (2,4) Принести шаблоны графиков функций: у = х2 , у =1/3 х2 , у =1/2 х2



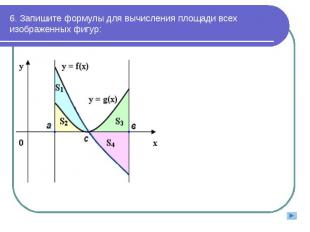
![Фигура, ограниченная снизу отрезком [a;b] оси Ох, сверху графиком непрерывной функции у = f(x), принимающей положительные значения, а с боков отрезками прямых х = а и х = b, называется криволинейной трапецией. Фигура, ограниченная снизу отрезком [a;… Фигура, ограниченная снизу отрезком [a;b] оси Ох, сверху графиком непрерывной функции у = f(x), принимающей положительные значения, а с боков отрезками прямых х = а и х = b, называется криволинейной трапецией. Фигура, ограниченная снизу отрезком [a;…](https://fs1.ppt4web.ru/images/95232/129669/640/img3.jpg)