Презентация на тему: Понятие площади фигуры и её измерение

Понятие площади фигуры и её измерение. Что такое площадь. Свойства площади. Какие фигуры называют равными. Какие фигуры называют равновеликими. Какие фигуры называют равносоставленными. Вспомните: Единицы измерения площади. Формулу площади прямоугольника, квадрата. Какая величина называется скалярной. Что такое палетка?

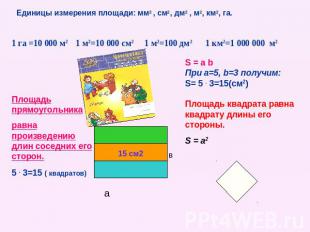
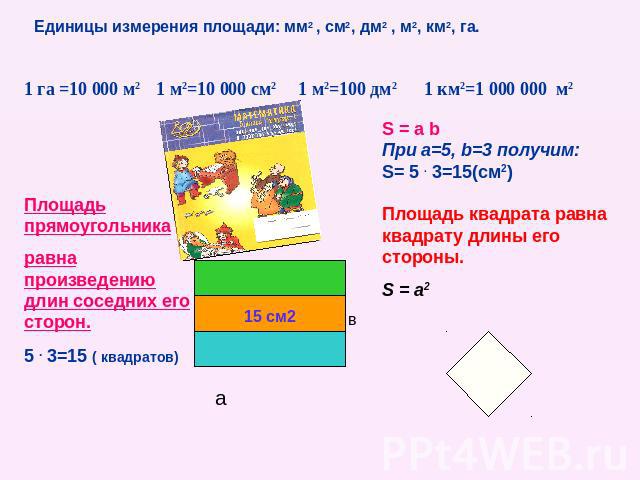
Единицы измерения площади: мм2 , см2, дм2 , м2, км2, га. 1 га =10 000 м2 1 м2=10 000 см2 1 м2=100 дм2 1 км2=1 000 000 м2 Площадь прямоугольника равна произведению длин соседних его сторон. 5 . 3=15 ( квадратов) S = a b При a=5, b=3 получим: S= 5 . 3=15(см2) Площадь квадрата равна квадрату длины его стороны. S = a2

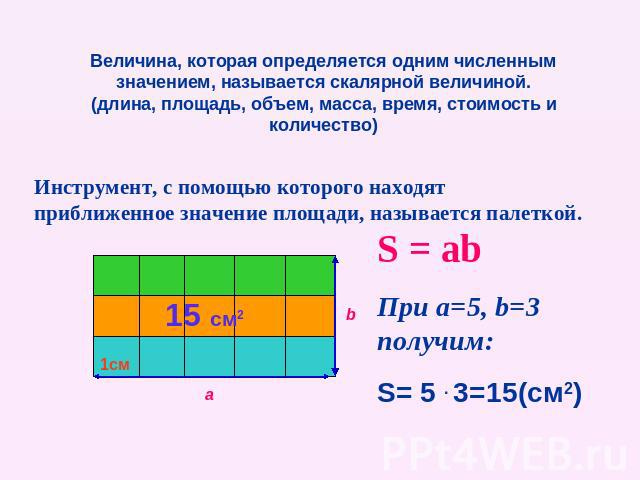
Величина, которая определяется одним численным значением, называется скалярной величиной. (длина, площадь, объем, масса, время, стоимость и количество) Инструмент, с помощью которого находят приближенное значение площади, называется палеткой. S = ab При a=5, b=3 получим: S= 5 . 3=15(см2)

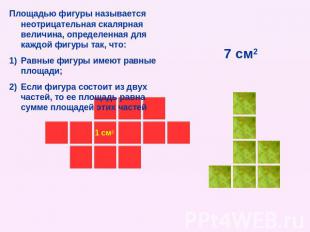
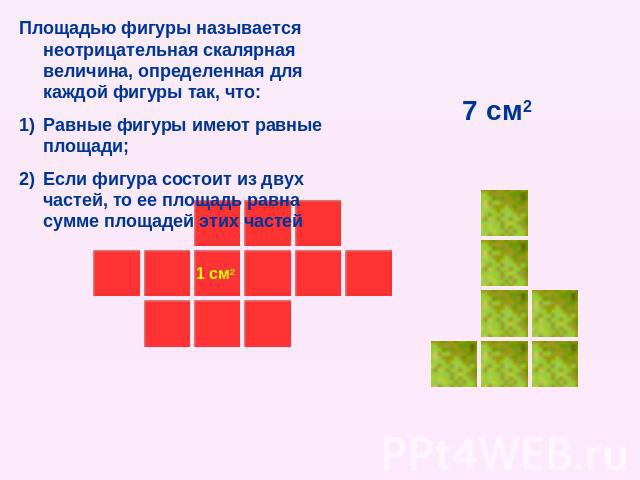
Площадью фигуры называется неотрицательная скалярная величина, определенная для каждой фигуры так, что: Равные фигуры имеют равные площади; Если фигура состоит из двух частей, то ее площадь равна сумме площадей этих частей

Свойства площадей плоских фигур. 1. Если фигуры равны, то равны численные значения их площадей, т. е. F1 = F2 ⇒ S(F1)=S(F2) 2. Если фигура F состоит из фигур F1 и F2 , то численное значение площади фигуры равно сумме численных значений площадей фигур F1 и F2 ,т.е. S(F1⊕F2)=S(F1)+S(F2) 3. Численное значение площади единичного квадрата принимается равным 1, т.е. S(E) =1. 4. При замене единицы площади численное значение площади фигуры F увеличивается ( уменьшается) во столько раз, во сколько новая единица меньше (дольше) старой. 5. Если фигура F1 является частью фигуры F2 ,то численное значение площади фигуры F1 не больше численного значения площади фигуры F2 , т.е. F1 ⊂ F2 ⇒ S(F1)≤S(F2)

ЗАДАЧА №1. Найдите площадь столешницы, длина которой равна 10дм, а ширина – 5см. Дано: a = 10дм, b = 5см. Найти S. Решение. S = a b. 10дм=100см. S = 100 * 5 =500(см2).

ЗАДАЧА №2 Длина школьного коридора равна 28м, а его ширина в 4 раза меньше. Чему равна площадь коридора? Дано: a = 28м, b – в 4 раза меньше Найти S. Решение. b = 28 : 4 = 7(м). S = 28 * 7 = 196(м2). Ответ: 196м2.

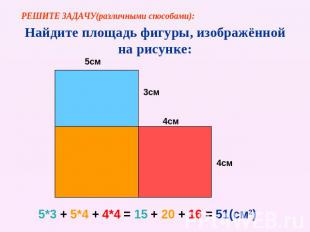
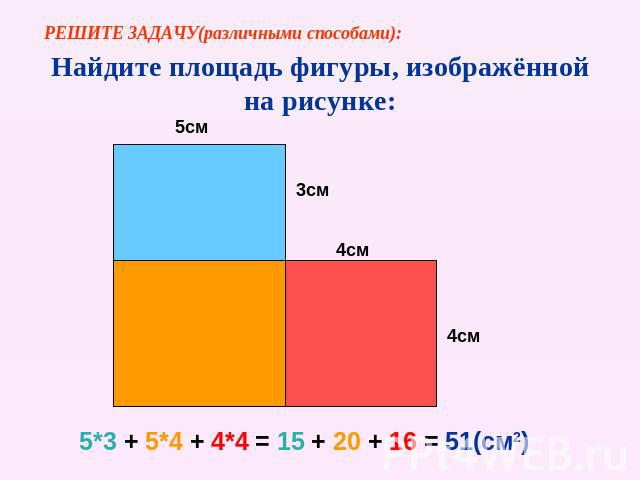
РЕШИТЕ ЗАДАЧУ(различными способами): Найдите площадь фигуры, изображённой на рисунке:

ЗАДАЧА №4 Найдите площадь полной поверхности куба. S = 4*4 = 16(cм2) S = a .a S = a2 Sn=6а2 S = 6*42 =96(cм2) Ответ: 96 см2

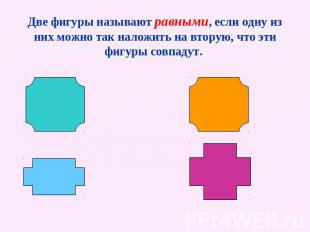
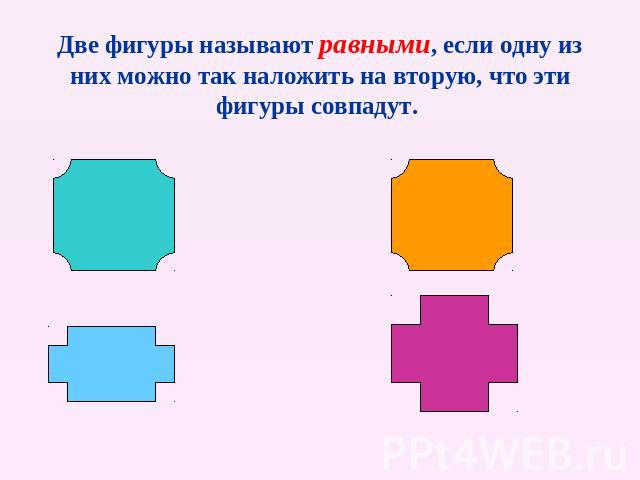
Две фигуры называют равными, если одну из них можно так наложить на вторую, что эти фигуры совпадут.

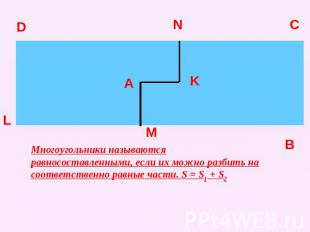
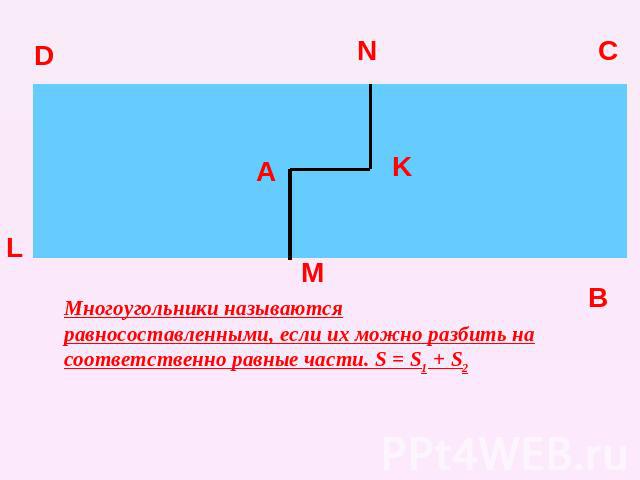
Многоугольники называются равносоставленными, если их можно разбить на соответственно равные части. S = S1 + S2

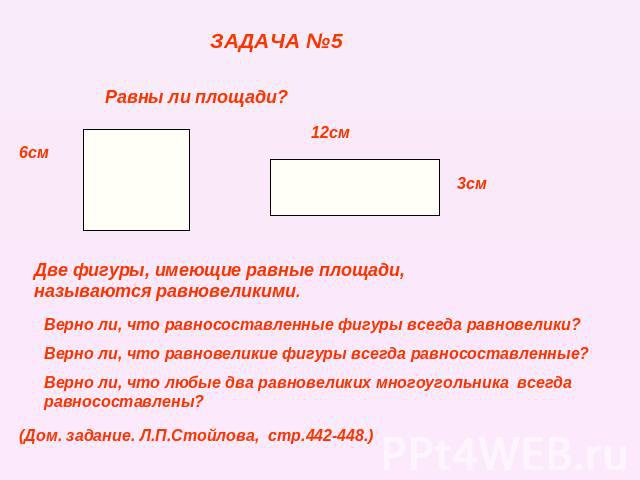
ЗАДАЧА №5 Равны ли площади? Две фигуры, имеющие равные площади, называются равновеликими. Верно ли, что равносоставленные фигуры всегда равновелики? Верно ли, что равновеликие фигуры всегда равносоставленные? Верно ли, что любые два равновеликих многоугольника всегда равносоставлены? (Дом. задание. Л.П.Стойлова, стр.442-448.)

Вычисли площадь фигур, если площадь каждой клетки равна 1см2. Алгоритм вычисления площади с помощью палетки. Наложить палетку на фигуру. Сосчитать число а целых клеток внутри фигуры. Сосчитать число в клеток, входящих в фигуру частично. Сосчитать приближенное значение площади: S ≈а+в:2(если число в нечетно, то увеличить или уменьшить его на 1).