Презентация на тему: Экстремум функции

Тема урока: «Признаки возрастания и убывания функции. Исследование функции на экстремум» 900igr.net

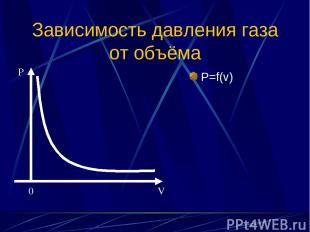
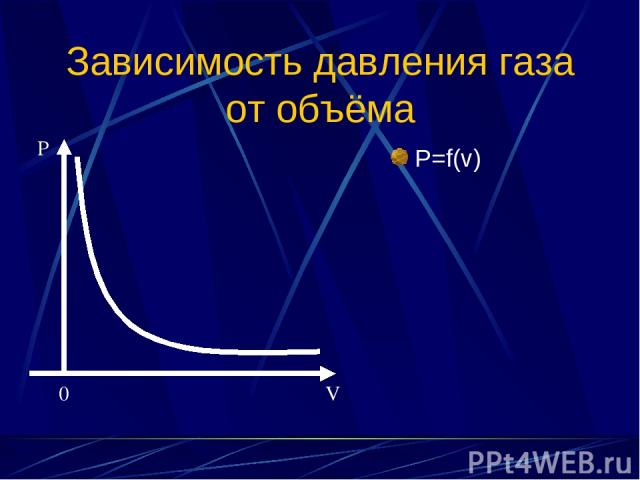
Зависимость давления газа от объёма P=f(v) P 0 V

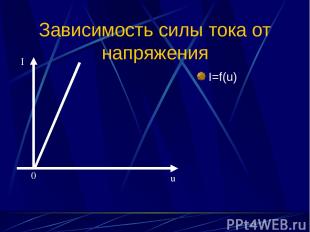
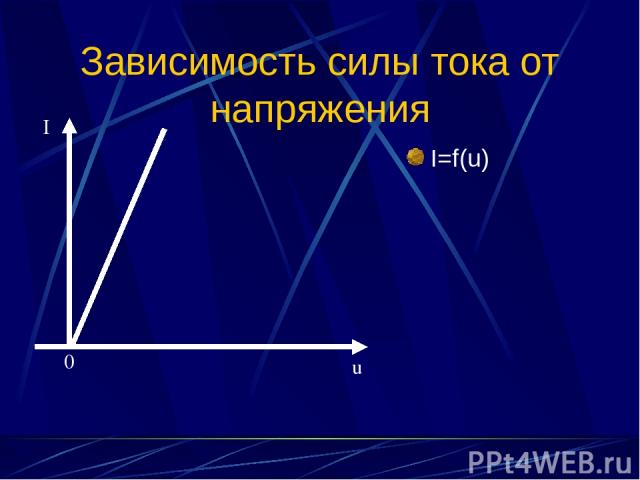
Зависимость силы тока от напряжения I=f(u) I 0 u

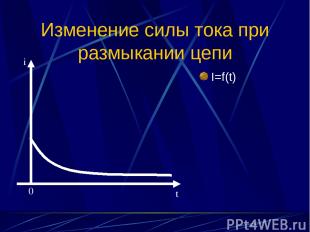
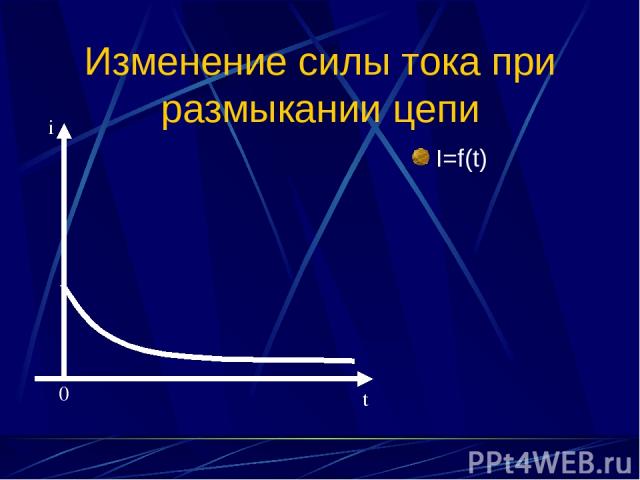
Изменение силы тока при размыкании цепи I=f(t) i 0 t

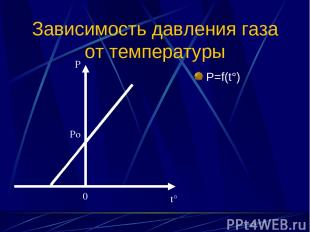
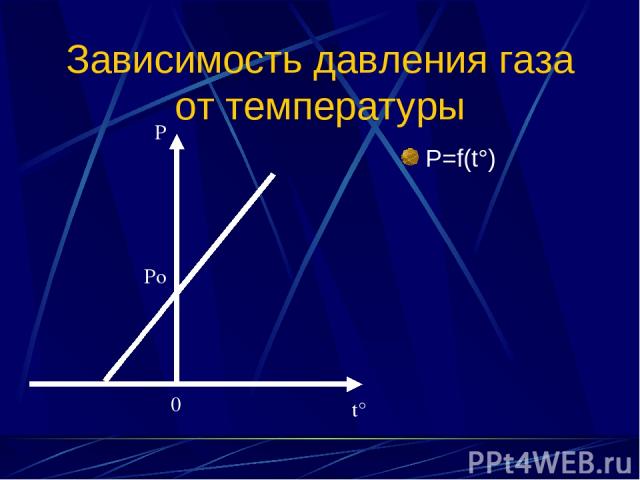
Зависимость давления газа от температуры P=f(t°) Po P 0 t°

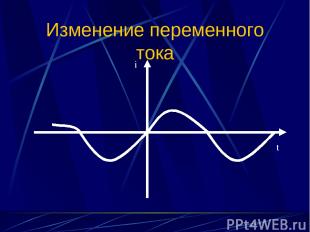
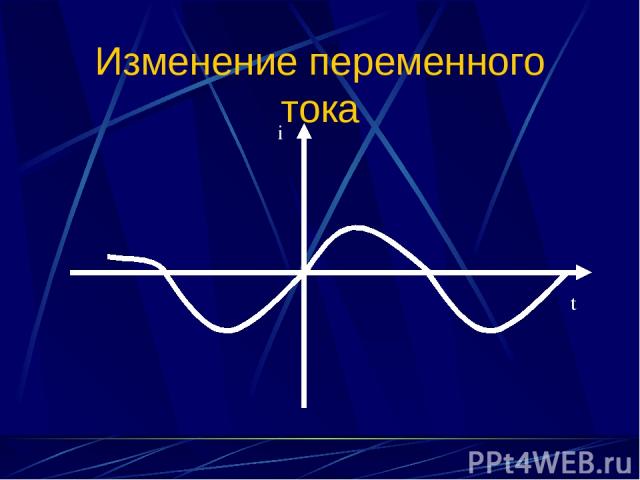
Изменение переменного тока i t

План: 1. Признаки возрастания и убывания функции. 2. Максимум и минимум функции (экстремум); необходимое и достаточное условия существования экстремума функции в точке. 3. Исследование функции на экстремум.

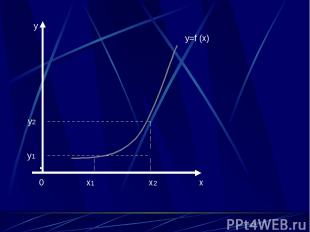
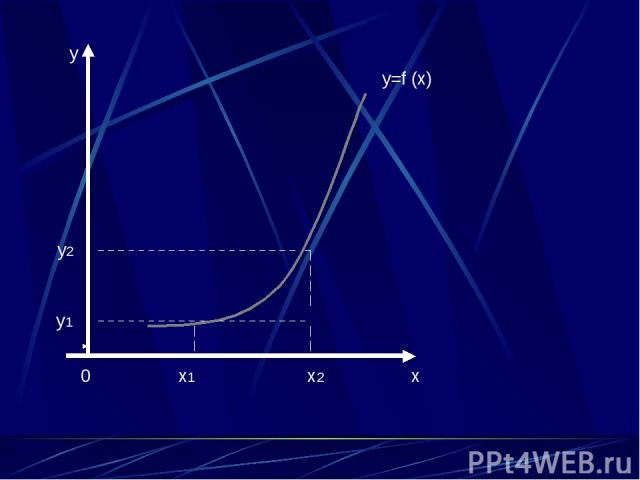
0 x1 x2 x y y1 y2 y=f (x)

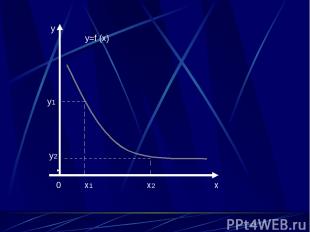
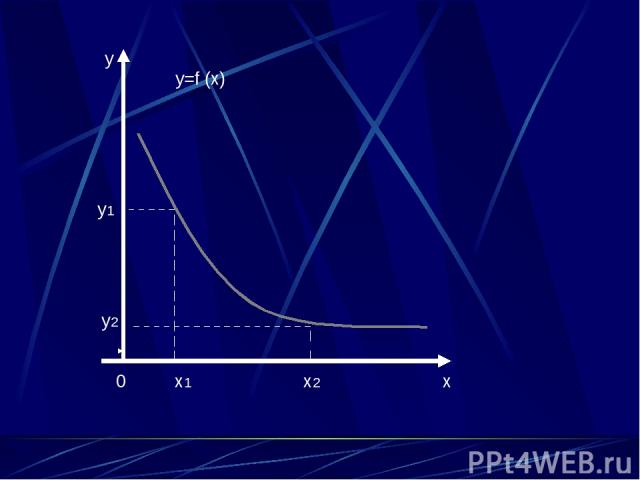
0 x1 x2 x y y2 y1 y=f (x)

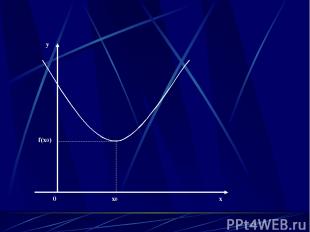
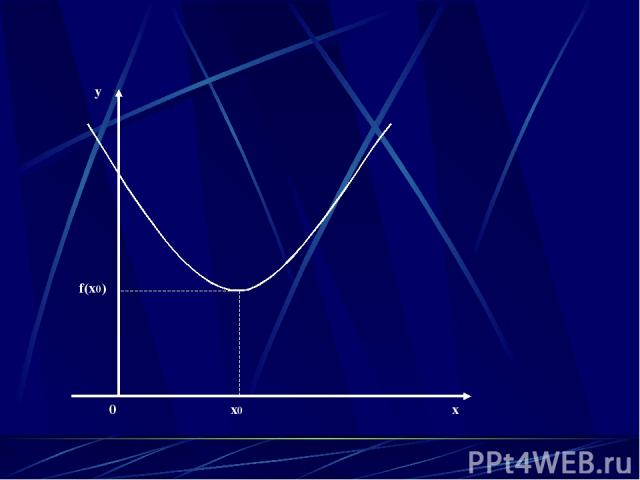
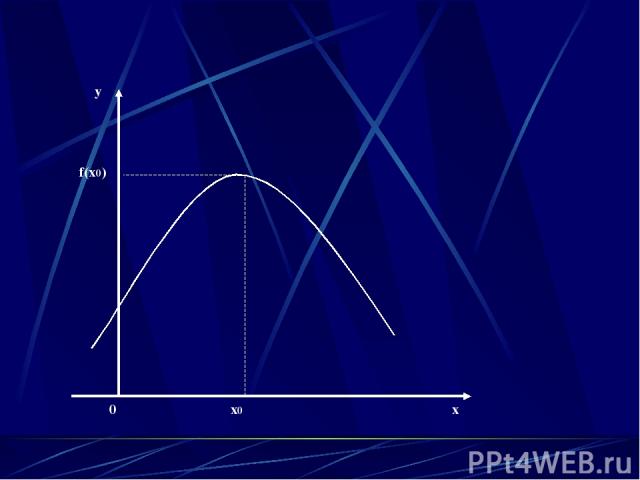
0 x0 x y f(x0)

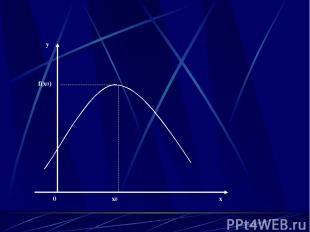
0 x0 x y f(x0)

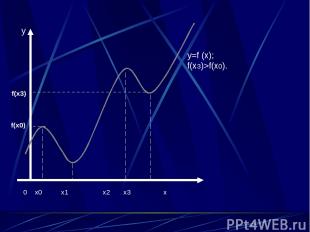
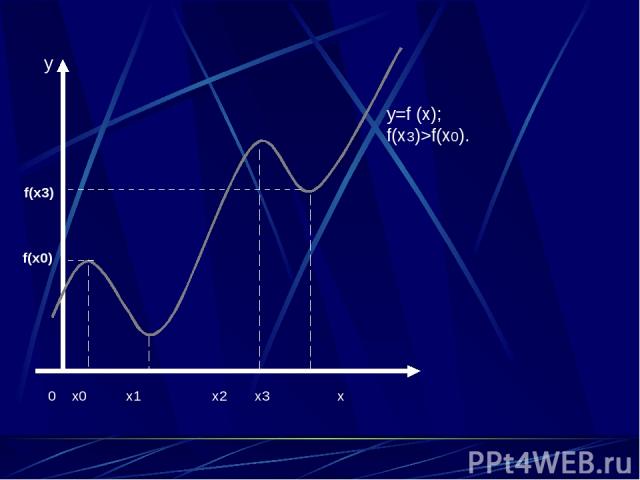
0 x0 x1 x2 x3 x y=f (x); f(x3)>f(x0). y f(x3) f(x0)

Тест. Тема: «Признаки возрастания и убывания функции. Исследование функции на экстремум»

1.Используя данные о функции y=f(x), определить промежутки в которых производная y' имеет отрицательные значения (см. таблицу) X Y -7 3 -3 -1 5 2 (- ∞ ; -7 ) ( -7 ; -3 ) ( -3 ; 5 ) ( 5 ; + ∞) Ответы: 1.(- ∞ ; -7)U(-3 ; 5); 2.(-7 ; -3); 3.(- ∞ ; 5); 4.(-7 ; -3)U(5 ; + ∞)

2. Укажите точки минимума функции y= (x),если данные о её производной указаны в таблице. x y + 0 - 0 + 0 - (- ∞ ; -1) -1 (-1 ; 5) 5 (5 ; 9) 9 (9 ; + ∞) Ответы: 1. Xo = 5; 2. Xo = 9; 3. Xo = -1; 4. Таких точек нет.

3.Определить промежутки возрастания функции y=f(x), используя данные о её производной y‘. (см. таблицу) x (- ∞ ; -9) -9 (-9 ; -1) -1 (-1 ; 3) 3 (3 ; + ∞) y' + 0 - 0 + 0 - Ответы: 1. (- ∞ ; 3); 2. (- ∞ ; -9) U (-1 ; 3) 3. (-9 ; -1) U (-1 ; 3); 4. (-9 ; + ∞)

4.Укажите точки максимума функции y=f(x), если данные о её производной y‘ указаны в таблице: X (-∞ ; -4) -4 (-4 ; 2) 2 (2 ; 8) 8 (8 ; +∞) y' – 0 + 0 - 0 + Ответы: 1. Xo = -4; 2. Xo = 8; 3. Xo = 2 4. Таких точек нет