Презентация на тему: Золотое сечение в математике и в жизни

Золотое сечениев математикеи в жизни Выполнила: Богомолова Оксана, ученица 11А класса МОУ СОШ №4, г.Нелидово Руководитель: Миловидова А.В.Учитель математики МОУ СОШ №4, г.Нелидово

« В геометрии существует два сокровища – теорема Пифагора и деление отрезка в крайнем и среднем отношении. Первое можно сравнить с ценность золота, второе можно назвать драгоценным камнем». Иоганн Кеплер

Задачи 1. Более подробно рассмотреть понятие «золотое сечение», история происхождения, алгебраическое нахождение «золотого сечения», геометрическое построение «золотого сечения».2. Рассмотреть применение «золотого сечения» в архитектуре Древней Греции.3. Рассмотреть «золотое сечение» как гармоническую пропорцию.4. Изучить такие понятия как «второе золотое сечение», «золотой треугольник».5. Постараться найти в окружающем меня мире применение этих понятий.

Цель Воспользовавшись различной литературой по геометрии, черчению, различными справочными материалами для более подробного изучения темы «золотое сечение», дать наиболее полное представление о данной теме; рассмотреть применение «золотого сечения» в архитектуре городов Тверской области.

Геометрическое определение"золотого сечения" Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему.

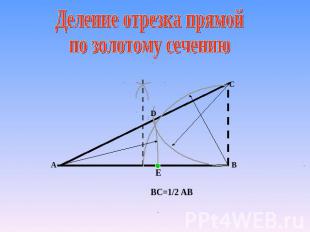
Деление отрезка прямой по золотому сечению

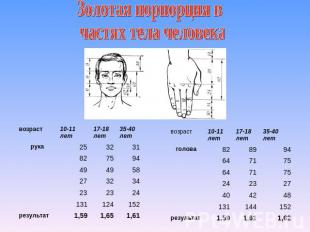
Золотая порпорция в частях тела человека

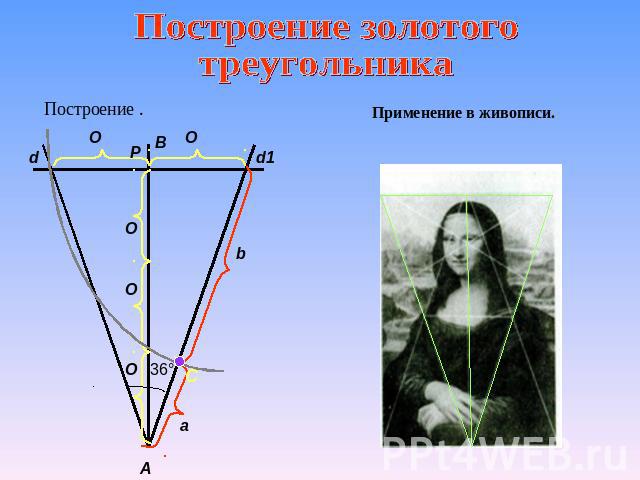
Построение золотого треугольника

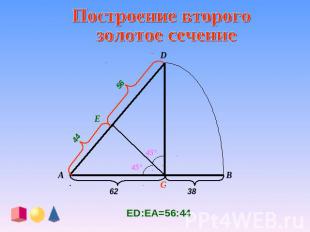
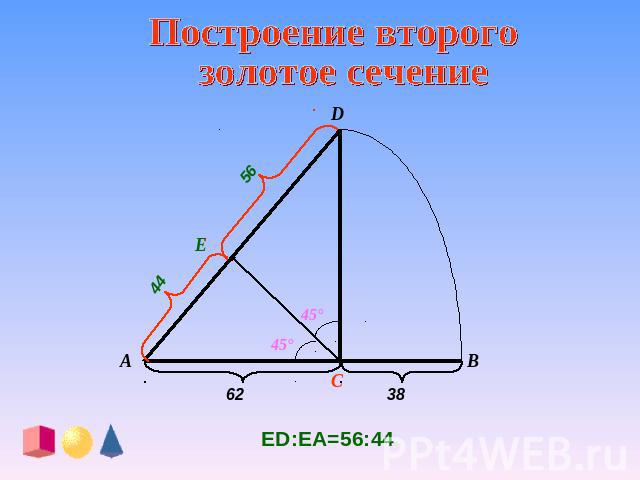
Построение второго золотое сечение

Применение "золотого" сеченияв архитектуре города Нелидова

Применение "золотого" сеченияв архитектуре города Старицы Успенский собор Церковь Иоанна Богослова

Приложение

Золотое сечение в архитектуре Парфенон Дворец культуры г.Нелидово

Золотое сечение в скульптуре Дорифор

Золотое сечение в музыке Ещё ничего не зная о природе звуков, человек интуитивно подстраивал струны так, чтобы они создавали благозвучие. Пифагору принадлежит математическое объяснение основ гармонии; по его определению, наиболее естественно воспринимаются человеком частоты, которые находятся между собой в простых числовых отношениях. Вот откуда и отношение частот в октаве 1: 2, и благозвучное трезвучие с отношением частот 4: 5: 6. Уменьшая последовательно длины струн, мы получим природный звукоряд из 16 звуков, но почему же древние музыканты приняли звукоряд, состоящий из семи основных звуков, и лишь позже добавили еще пять дополнительных (так появились черные клавиши в пианино).Значение работ Пифагора по научному объяснению основ музыкальной гармонии трудно переоценить. Это была первая научно обоснованная теория гармонии в музыке. Познав истинность и красоту своей музыкальной теории, Пифагор пытался распространить ее на космологию; по его представлениям, и планеты Солнечной системы располагались в соответствии с музыкальной октавой. Эта гипотеза Пифагора не потеряла своей привлекательности и в более поздние времена.

Золотое сечение в биологии Цветки и семена подсолнуха, ромашки, чешуйки в плодах ананаса, хвойных шишках "упакованы" по логарифмическим спиралям, завивающимся навстречу друг другу. Причем числа "правых "и "левых " спиралей, всегда относятся друг к другу, как соседние числа Фибоначчи В формулах листорасположения (филлотаксис) многих растений встречаются числа Фибоначчи, расположенные строго закономерно - через одно, например, орешник -1/3, дуб, вишня - 2/5, облепиха-5/13

Золотое сечение в живописи На знаменитой картине И.И.Шишкина «Сосновая роща» с очевидностью просматриваются мотивы золотого сечения. Ярко освещенная солнцем сосна (стоящаяна первом плане) делит длину картины по золотому сечению. Справа от сосны - освещённыйсолнцем пригорок. Он делит по золотому сечению правую часть картины по горизонтали. Слева от главной сосны находится множество сосен - при желании можно с успехом продолжить деление картины по золотому сечению и дальше.

Золотое сечение в физике Ускорение силы тяжести при удалении от земной поверхности описывается следующей формулой: где h - высота над поверхностью Земли, R - ее радиус. При опускании тела в глубь Земли характер зависимости g от h меняется: Когда gh=g-h? Ясно, что одним из решений будет h=0. Второе решение таково: Мы видим в решении уже знакомую нам формулу золотого сечения.

Золотое сечение в построении снежинок Золотое сечение присутствует в строении всех кристаллов, но большинство кристаллов микроскопически малы, так что мы не можем разглядеть их невооруженным глазом. Однако снежинки, также представляющие собой водные кристаллы, вполне доступны нашему взору. Все изысканной красоты фигуры, которые образуют снежинки, все оси, окружности и геометрические фигуры в снежинках также всегда без исключений построены по совершенной четкой формуле золотого сечения.