Презентация на тему: Знаменитые задачи древности. Трисекция угла

Научно-исследовательская работа по математике: «Знаменитые задачи древности. Трисекция угла».

Выполнил: ученик 6 класса Зеленин НикитаРуководитель:учитель математикиЛевищенко О. П.Образовательное учреждение:МОУ «Средняя общеобразовательная школа № 59» г. Курска

План работы: 1. Введение2. Историческая справка3. Решение Древних греков4. Решение пифагорейцев5. Решение Архимеда6. Решение по системе «ПОКО»7. Ещё один метод решения задачи8. Доказательство невозможности9. Заключение10. Список литературы

Математические задачи, возникающие в жизни и в практической деятельности людей, в технике, и в науке, в том числе и в математике, весьма многочисленны и многообразны.Среди математических задач есть такие, которые пользуются популярностью; им со временем присвоили эпитеты: «знаменитые», «коварные», «неподдающиеся» и т.п.Особенно большое внимание привлекали к себе в течение многих веков задачи, которые с давних времён известны как «знаменитые задачи древности». Под этим названием обычно формулировали три знаменитые задачи: 1. Квадратура круга;2. Трисекция угла;3. Удвоение куба.Некоторые авторы причисляют к ним ещё две задачи эпохи античности: деление окружности на равные части (построение правильных многоугольников) и квадратура луночек.Все эти задачи возникли в глубокой древности из практических потребностей людей. На первом этапе своего существования они выступали как вычислительные задачи: по некоторым правилам вычислялись приближённые значения искомых величин.

В древней Греции этим задачам придали классические формулировки:1. разделить данный угол на три равные части;2. построить квадрат, равновеликий данному кругу;3. построить ребро нового куба, объём которого был бы в 2 раза больше данного куба;4. построить правильный п- угольник (разделить окружность на п равных частей);5. построить прямолинейную фигуру, равновеликую данной круговой луночке.Эти задачи пытались решить методами геометрической алгебры, а именно: с помощью циркуля и линейки.Простота формулировок этих задач и непреодолимые трудности, возникшие на пути их решения, способствовали росту их популярности. Над ними бились лучшие геометрические умы. Затем им отдавали силы арабские математики. В течение столетий лучшие европейские математики трудились над решением задач античности. Пытаясь найти строгие решения указанных задач, учёные получали «попутно» многие важные результаты для математики.

Впервые о знаменитых задачах математики я услышал от нашего учителя математики на факультативном занятии «Наглядная геометрия». Мне захотелось узнать: чем же знамениты эти задачи? Почему я до сих пор о них ничего не знаю? Кто автор этих задач?Возникшие вопросы определили цели и задачи моей работы.Цель исследования: рассмотреть подробно одну из знаменитых задач математики.Объект исследования: задача о трисекции угла.Предмет исследования: значимость данной задачи в математике, в жизни.Гипотеза: знаменитые задачи античности имеют важное значение в развитии математики и носят практическую значимость до сих порпри решении, составлении задач, применении на практике. Цель, предмет и гипотеза исследования определили постановку следующих задач: 1) изучить различные источники информации по вопросу о трисекции угла;2) рассмотреть историю возникновения знаменитых задач;3) познакомиться с различными способами решения задачи о трисекции угла; 4) проанализировать роль и место знаменитых задач в развитии математики и их применение на практике.

2. Историческая справка Деление любого угла на три равные части называют трисекцией угла. Задача трисекции угла возникла в Древней Греции, примерно в V веке до н.э. из потребностей архитектуры и строительной техники. Древним грекам удалось решить задачу о трисекции прямого угла при помощи циркуля и линейки.Можно построить треть прямого угла: поделив пополам угол правильного треугольника. А, проведя биссектрису в образовавшемся угле в 30˚, получим угол величиной 15˚ - треть угла в 45˚. Есть и другие углы, для которых трисекция выполнима. Наверное, подобные построения и вселили надежду открыть способ трисекции любого угла посредством циркуля и линейки. В дальнейшем было также доказано, что угол вида a = p /2n, где n N , можно разделить на три равные части. Р. Декарт высказал предположение о неразрешимости задачи о трисекции произвольного угла при помощи циркуля и линейки без засечек.Это утверждение было доказано в 1837 году Ванцелем.В 15 веке самаркандский ученый применил трисекцию угла к составлению весьма точных тригонометрических таблиц. В 16 веке французский математик Ф. Виет на основе трисекции угла нашел тригонометрическое решение квадратного уравнения при помощи циркуля и линейки без засечек. Задачу на трисекцию угла можно решить, если угол равен:1. 90°, 45°, 22,5°,... p /2n, где n N (все эти углы образуют бесконечно малую геометрическую прогрессию со знаменателем q =1/2). 2. 180°. 3. 360°.

3. Решение Древних греков Из приведенной таблицы видно, что задача трисекции угла в 90 градусов разрешима. Любой острый угол нельзя разделить на 3 равные части при помощи циркуля и линейки, а углы a = p /2n, где nI N можно.

4. Решение пифагорейцев  Деление прямого угла на три равные части умели производить ещё пифагорейцы, основываясь на том, что в равностороннем треугольнике каждый угол равен 60°. Пусть требуется разделить на три равные части прямой угол MAN, откладываем на полупрямой AN произвольный отрезок AC, на котором строим равносторонний треугольник ACB. Так как угол CABравен 60°, то угол BAM равен 30°. Построим биссектрису AD             угла САВ, получаем искомое деление прямого угла MANна три равных угла: NAD, DAB, BAM.Задача о трисекции угла оказывается разрешимой и при некоторых других частных значениях угла (например, для углов в 90°/2n, n – натуральное число), однако не в общем случае, т.е. любой угол невозможно разделить на три равных части с помощью только циркуля и линейки. Это было доказано лишь в первой половине ХIХ в.    Задача о трисекции угла становится разрешимой и общем случае, если не ограничиваться в геометрических построениях одними только классическими инструментами, циркулем и линейкой.

5. Решение Архимеда Решение Архимеда            Рис. 4                                                          Рис. 5Интересное решение задачи о трисекции угла дал Архимед в своей книге «Леммы», в которой доказывается , что если продолжить хорду AB (рис.4) окружности радиуса r на отрезок BC = r и провести через С диаметр FE , то дуга BF будет втрое меньше дуги АЕ. Действительно на основе теорем  о внешнем угле треугольника и о равенстве углов при основании равнобедренного треугольника имеем:                        AOE = OAB + ACO,                OAB = ABO, ACO = BOCзначит, AOE = 3 BOC                                     Отсюда следует так называемый способ «вставки» для деления на три равные части угла AOE. Описав окружность с центром O и  радиусом  и , проводим диаметр . Линейку CB на которой нанесена длина  радиуса r (например,  помощью двух штрихов), прикладываем и двигаем так, чтобы её точка C скользила по продолжению диаметра , а сама линейка всё время проходила бы через точку A окружности, пока точка B линейки не окажется на окружности. Тогда угол BCF и будет искомой третьей частью угла AOE (Рис.5). Как видно, в этом приёме используется вставка отрезка CB между продолжением диаметра EF и окружностью так, чтобы продолжение отрезка CB прошло через заданную точку A окружности. В указанном выше построении применяется, помимо циркуля, не просто линейка как инструмент для проведения прямых, а линейки с  делениями, которая даёт длину определённого отрезка.

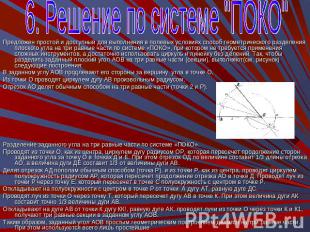
6. Решение по системе "ПОКО" Предложен простой и доступный для выполнения в полевых условиях способ геометрического разделения плоского угла на три равные части по системе «ПОКО», при котором не требуется применения сложных инструментов, а достаточно использовать циркуль и линейку без делений. Так, чтобы разделить заданный плоский угол АОВ на три равные части (секции), выполняют(см. рисунок) следующие построения:В заданном углу АОВ продлевают его стороны за вершину угла в точке О.Из точки О проводят циркулем дугу АВ произвольным радиусом.Отрезок АО делят обычным способом на три равные части (точки 2 и Р).Разделение заданного угла на три равные части по системе «ПОКО».Проводят из точки О, как из центра, циркулем дугу радиусом ОР, которая пересечет продолжение сторон заданного угла за точку О в точках Д и Е. При этом отрезок ОД по величине составит 1/3 длины отрезка АО, а величина дуги ДЕ составит 1/3 от величины дуги АВ.Делят отрезок АД пополам обычным способом (точка Р), и из точки Р, как из центра, проводят циркулем полуокружность радиусом АР, которая пересечет продолжение отрезка АО в точке Д. Проводят луч из точки Р через точку Е, который пересечет в точке С полуокружность с центром в точке Р.Откладывают на полуокружности с центром в точке Р от точки А дугу АТ, равную дуге ДС.Проводят луч из точки О через точку Т, который пересечет дугу АВ в точке К. При этом величина дуги АК составит точно 1/3 величины дуги АВ.Откладывают на дуге АВ от точки К дугу КК!, равную дуге АК, проводят лучи из точки О через точки К и К1, получают три равные секции в заданном углу АОВ.Таким образом, заданный угол АОВ простым геометрическим построением делится на три равные части. При этом используются всего лишь простейшие

Алгоритм решения задачи:1. С помощью циркуля определяются точки В и С таким образом, что АВ=АС2. Проводится прямая через точки ВС3. В точке С строится перпендикуляр к прямой ВС4. Определяется точка D таким образом, что ВС=СD5. В прямоугольном треугольнике ВСD опускаем перпендикуляр на гипотенузу DВ (получаем точку Е и прямоугольный треугольнике СЕВ)6. Из точки В проводим прямую параллельную отрезку ЕС7. На этой прямой находим точку F таким образом, что ВF=2*ЕС8. Проводим отрезок ЕF, определяя точку G, так как угол СЕF=30гр., то отрезок СG=ВС/39. Поделить отрезок ВG на две равные части не составляет никакого труда, таким образом, задача трисекции угла решена.

8. Доказательство невозможности Уже в умах древнегреческих математиков зародилась мысль о том, что средствами геометрической алгебры эти задачи не разрешить. И лишь в 19 веке было строго доказано, что все эти задачи неразрешимы с помощью циркуля и линейки.Французский математик П. Ванцель в 1837 г. первым строго доказал, что невозможно осуществить трисекцию циркулем и линейкой. Пусть β = α/3. По известной формуле, соs 3α = = 4 соs3 β - 3 соs β. Тогда для величины х = 2 соs β получается уравнение x3 – 3x - а = 0, где а = 2 соs α . Геометрическая задача трисекции данного угла а циркулем и линейкой разрешима тогда и только тогда, когда полученное алгебраическое уравнение разрешимо в квадратных радикалах. Возьмём, например, α = 60°. Тогда уравнение примет вид х3 – 3x - 1 = 0. Оно неразрешимо в квадратных радикалах, а потому и трисекция с помощью циркуля и линейки в данном случае невозможна. Тем более она невозможна в общем случае. Интересно, что вообще для углов вида З60°/n с целым п трисекцию удаётся осуществить тогда и только тогда, когда n не делится на 3. Задача о трисекции угла в общем случае не разрешима при помощи циркуля и линейки, но это вовсе не значит, что данную задачу нельзя решить другими вспомогательными средствами.

Первый из древнегреческих учёных, кто дал строгое решение задачи о трисекции любого острого угла при помощи дополнительных вспомогательных средств, был Гипий из Элиды. Он применил для решения задачи о трисекции угла трансцендентную кривую, которую позже Лейбниц назвал в 17 веке квадратрисой.Вспомогательные средства использовали и другие учёные Древней Греции. Так, например, Никомед во 2 веке до н. э. открыл кривую Конхоиду и применял её при решении задач трисекции угла и удвоения куба.Но построить конхоиду Никомеда было достаточно сложно. Поэтому для решения задачи трисекции угла использовали метод вставок, положив в основу идеи Никомеда.Таким образом, учёным Древней Греции удалось найти строгое решение задачи трисекции угла, но только с помощью дополнительных вспомогательных средств.Другие весьма оригинальные, но довольно сложные способы решения задачи о трисекции угла дали учёные Декарт, Ньютон, Клеро, Шаль. Все эти решения основаны на отыскании точек пересечения конического сечения с окружностью.

А впервые использовал конические сечения для решения задачи о трисекции угла Папа Александрийский.Для достижения указанной цели придумано много механических приборов, которые называются трисекторами. Простейший трисектор легко изготовить из плотной бумаги, картона или тонкой жести. Он послужит подсобным чертёжным инструментом.Трисектор и схема его применения. На рис. 143 трисектор изображен в натуральную величину (заштрихованная фигура). Примыкающая к полукругу полоска АВ равна по длине радиусу полукруга. Край полоски ВD составляет прямой угол с прямой АС; он касается полукруга в точке В; длина этой полоски произвольна. На том же рисунке показано употребление трисектора. Пусть, например, требуется разделить на три равные части угол КSМ.

Трисектор помещают так, чтобы вершина угла S находилась на линии ВD, одна сторона угла прошлачерез точку А, а другая сторона коснулась полукруга. Затем проводят прямые SВ и SО, и деление данного угла на три равные части окончено. Для доказательства соединим отрезком прямой центр полукруга О с точкой касания N. Легко убедиться в том, что треугольник АSВ равен треугольнику SВО, а треугольник SВО равен треугольнику OSN. Из равенства этих трех треугольников следует, что углы АSВ, ВS0 и 0SN равны между собой, что и требовалось доказать.Такой способ трисекции угла не является чисто геометрическим; его скорее можно назвать механическим.

Итак, было доказано, что знаменитые задачи невозможно решить только циркулем и линейкой. Но ужу постановка задачи – «доказать неразрешимость» - была смелым шагом вперёд. Вместе с тем предлагалось множество решений при помощи нетрадиционных инструментов. Всё это привело к возникновению и развитию совершенно новых идей в геометрии и алгебре.Немало преуспели в нестандартных и различных приближённых решениях любители математики – среди них 3 знаменитые задачи древности особенно популярны. Задачи кажутся доступными любому: вводят в заблуждение их простые формулировки.До сих пор редакции математических журналов время от времени получают письма, авторы которых пытаются опровергнуть давно установленные истины и подробно излагают решение какой – либо из знаменитых задач с помощью циркуля и линейки. Изучив различные информационные источники по данному вопросу, я достиг поставленной цели: 1) узнал формулировки знаменитых задач, их суть;2) проследил историю развития известных задач;3) открыл для себя имена учёных – математиков, занимавшихся «коварными задачами»;4) научился применять методы геометрической алгебры для решения задач.

Моя гипотеза о важности древних задач, их применении в практической деятельности – подтвердилась. С пользой прошло время сбора материала по теме. Я научился выбирать главное из обилия литературы, сравнивать различные способы решения задач, систематизировать материал. Попытки решить эти задачи с помощью методов геометрической алгебры способствовали попутным открытиям математиков, изготовлению различных технических приспособлений, помогающих разделить угол на 3 равные части.Заинтересовали меня и другие знаменитые задачи: о квадратуре круга, удвоении куба. Некоторые мои одноклассники занимались изучением этих задач. В дальнейшем мы планируем выступить со своими исследовательскими работами перед учениками – любителями математики, во время предметной недели математики, традиционно проводимой в нашей школе.

10. Литература и источники из Интернета: «Энциклопедия для детей. Математика» Аванта+ Москва 2004г., с. 321-322.http:// demo.karelia.ruhttp:// cultinfo.ruhttp:// inventors.ru