Презентация на тему: Введение в мир фракталов

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ МОРДОВИЯМОУ «ИНСАРСКАЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА №1» Конкурс научно – исследовательских работ «Интеллектуальное будущее Мордовии» Секция: математика ВВЕДЕНИЕ В МИР ФРАКТАЛОВ Автор работы: ЯМАШКИН ПАВЕЛ,

ЦЕЛЬ РАБОТЫ исследование и изучение основ фрактальной теории, знакомство с математическим обоснованием графической интерпретации фрактальных образов МЕТОДЫ ИЗУЧЕНИЯ Анализ литературы по теме исследования, Изучение фракталов различного вида, Разработать классификацию фракталов, Собрать коллекцию фрактальных образов.

ОСНОВНЫЕ НАПРАВЛЕНИЯ РАБОТЫ

ПОНЯТИЕ ФРАКТАЛА Фрактал - геометрическая фигура, состоящая из частей, которые могут быть поделены на части, каждая из которых будет представлять уменьшенную копию целого. Fractal от латинского слова fractus, означает разбитый (поделенный на части).Основное свойство фракталов: самоподобие, в самом простом случае небольшая часть фрактала содержит информацию о всем фрактале.

ФРАКТАЛЫ В ПРИРОДЕ

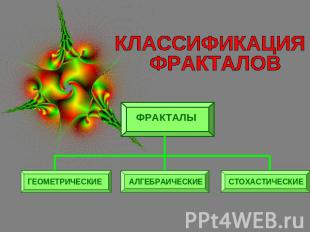
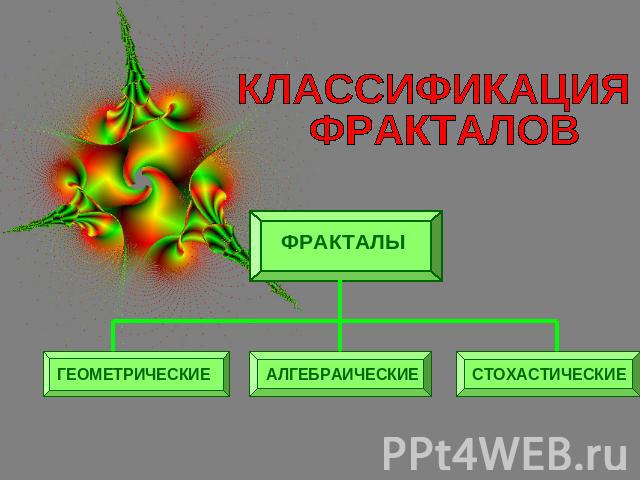
КЛАССИФИКАЦИЯ ФРАКТАЛОВ

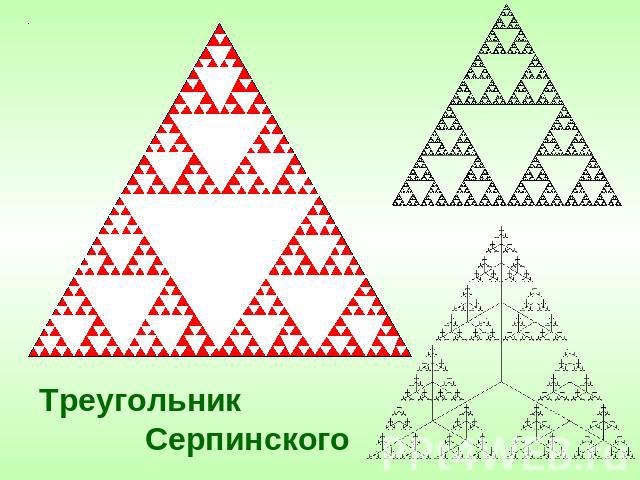
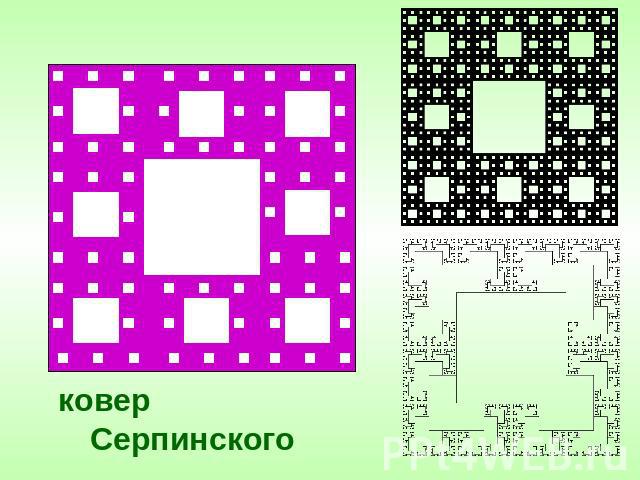
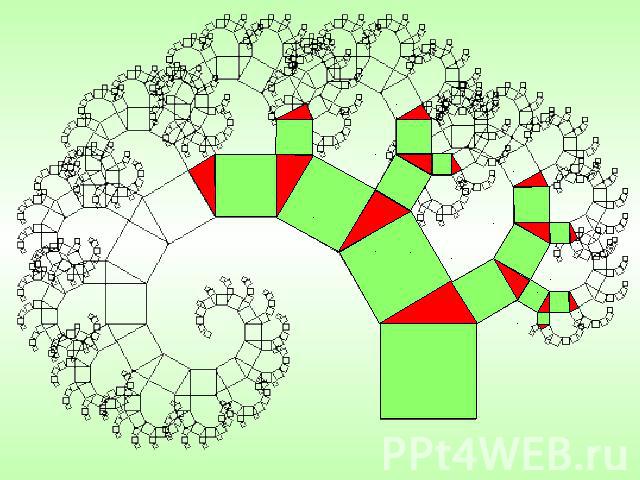
ГЕОМЕТРИЧЕСКИЕ ФРАКТАЛЫ Это «функции - монстры», которых так называли за недифференцируемость в каждой точке. Геометрические фракталы являются также самыми наглядными, т.к. сразу видна самоподобность. Для построения геометрических фракталов характерно задание «основы» и «фрагмента», повторяющегося при каждом уменьшении масштаба.

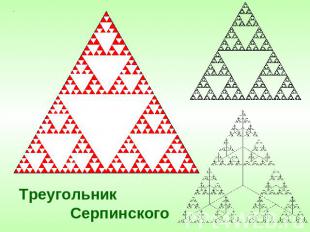
Треугольник Серпинского

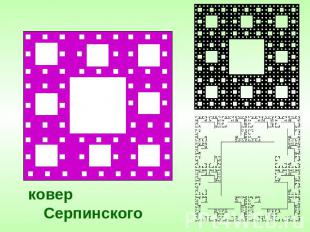
ковер Серпинского

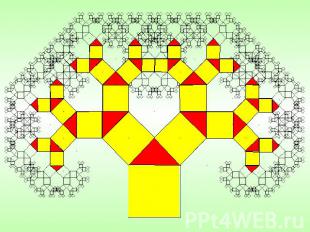
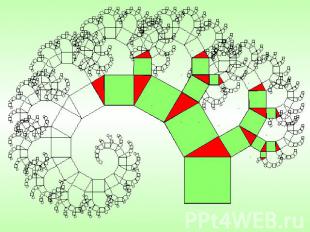
АЛГЕБРАИЧЕСКИЕ ФРАКТАЛЫ Это фракталы, которые можно построить, используя простые алгебраические формулы.Получают их с помощью нелинейных процессов в n–мерных пространствах.Самыми известными из них являются множества Мандельброта и Жюлиа, Бассейны Ньютона

Множество Жюлиа Цвет каждой точки зависит от того, сколько итераций комплексной функцииможет быть сделано, пока точка z не выйдет за пределы круга радиуса r  Здесь z — комплексное число, соответствующее точке . Множество Жюлиа — это множество таких точек, что отображения видане отображают их в окрестность бесконечности. На рисунке эти точки окрашены лиловым цветом.Картинка получена выбором параметровa = 1.8, и b = 0.2 i и поворотом на 900

МНОЖЕСТВО МАНДЕЛЬБРОТА (окрашено лиловым цветом). Картинка получается с помощью той же процедуры, что и выше. Различие состоит в том, что начальное значение для точки z берётся всегда равным нулю, а точке с координатами (х; у) на картинке соответствует комплексный параметр b = x + y i.

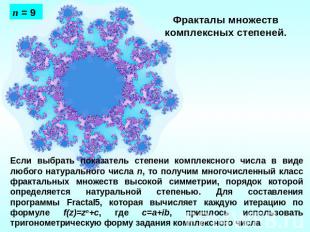
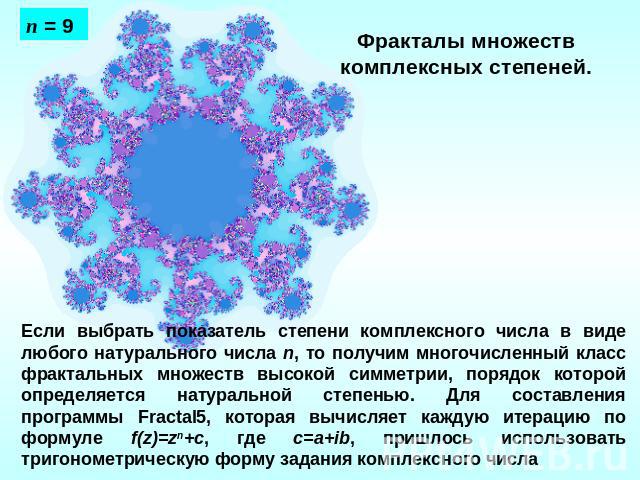
Фракталы множеств комплексных степеней. Если выбрать показатель степени комплексного числа в виде любого натурального числа n, то получим многочисленный класс фрактальных множеств высокой симметрии, порядок которой определяется натуральной степенью. Для составления программы Fractal5, которая вычисляет каждую итерацию по формуле f(z)=zn+c, где с=a+ib, пришлось использовать тригонометрическую форму задания комплексного числа

СТОХАСТИЧЕСКИЕ ФРАКТАЛЫ Это фракталы, при построении которых в итеративной системе случайным образом изменяются какие-либо параметры.Эти фракталы используются при моделировании рельефов местности и поверхности морей, процесса электролиза.Стохастические фракталы очень похожи на природные объекты – несимметричные деревья, изрезанные береговые линии.

Фрактальная наука еще очень молода, и ей предстоит большое будущее. Красота фракталов далеко не исчерпана и еще подарит нам немало шедевров- тех, которые услаждают глаз, и тех, которые доставляют истинное наслаждение разуму. ПРИМЕНЕНИЕ ФРАКТАЛОВ

ЗАКЛЮЧЕНИЕ 1. Проанализирована и проработана литература по теме исследования.2. Рассмотрены и изучены различные виды фракталов.3. Представлена классификация фракталов.4. Собрана коллекция фрактальных образов для первичного ознакомления с миром фракталов.5. Составлены программы для построения графического образа фракталов.