Презентация на тему: Три основные задачи на проценты

Три основные задачи на процентыНахождение процента от числаНахождение числа по его процентуНахождение процентного отношения двух чисел

1. Нахождение процента от числаЧтобы найти 0,01p от a, надо a умножить на 0,01p b=a 0,01pЧтобы найти процент от числа, надо это число умножить на соответствующую дробь.Например, 20% от 45 кг равны 45 0.2=9 кг, а 118% от x равны 1.18x.

2. Нахождение числа по его проценту Чтобы найти число по его части b, выраженной дробью 0,01p, надо b разделить на 0,01pa=b : 0,01pЧтобы найти число по его проценту, надо часть, соответствующую этому проценту, разделить на дробь.Например, 8% длины отрезка составляют 2,4 см, то длина всего отрезка равна 2,4:0,08=30см

3. Нахождение процентного отношения двух чиселР = (b:a) 100%Чтобы найти, сколько процентов число b составляет от a, надо сначала узнать, какую часть b составляет от a, затем эту часть выразить в процентах %.Чтобы узнать, сколько процентов одно число составляет от второго, надо первое число разделить на второе и результат умножить на 100%.Например, 9 г соли в растворе массой 180 г составляют (9 100):180=5% раствора.

Решение задач на смеси и сплавыТаблица для решения задач имеет следующий вид: 

Задача 1. В сосуд содержащий 2 кг 80 % -го водного раствора уксуса добавили 3 кг воды. Найдите концентрацию получившегося раствора уксусной кислоты.Масса уксусной кислоты не изменилась

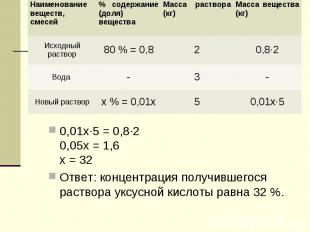
0,01х·5 = 0,8·2 0,05х = 1,6х = 32Ответ: концентрация получившегося раствора уксусной кислоты равна 32 %.

Задача 2.Сколько нужно добавить воды в сосуд, содержащий 200 г 70 % -го раствора уксусной кислоты, чтобы получить 8 % раствор уксусной кислоты?

Задача 3. Смешали некоторое количество 12% раствора соляной кислоты с таким же количеством 20 % раствора этой же кислоты. Найти концентрацию получившейся соляной кислоты. Ответ : концентрациясоляной кислоты16%

Задача 4. Смешали 8кг 18 % раствора некоторого вещества с 12 кг 8 % раствора этого же вещества. Найдите концентрацию получившегося раствора.

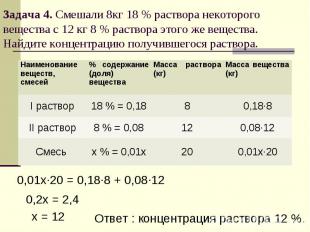
Задача 4. Смешали 8кг 18 % раствора некоторого вещества с 12 кг 8 % раствора этого же вещества. Найдите концентрацию получившегося раствора.

Задача 5 Смешав 40 % и 15 % растворы кислоты, добавили 3 кг чистой воды и получили 20 % раствор кислоты. Если бы вместо 3 кг воды добавили 3 кг 80 % раствора той же кислоты, то получили бы 50 %-ый раствор кислоты. Сколько килограммов 40 % -го и 15 % растворов кислоты было смешано?.

выполним вторую операцию Смешав 40 % и 15 % растворы кислоты, добавили 3 кг чистой воды и получили 20 % раствор кислоты. Если бы вместо 3 кг воды добавили 3 кг 80 % раствора той же кислоты, то получили бы 50 %-ый раствор кислоты. Сколько килограммов 40 % -го и 15 % растворов кислоты было смешано?. 0,4х + 0,15у + 0,8·3 = 0,5(х + у +3).

Для решения задачи получаем систему уравнений:Ответ:3,4 кг 40 % кислоты и 1,6 кг 15 % кислоты.