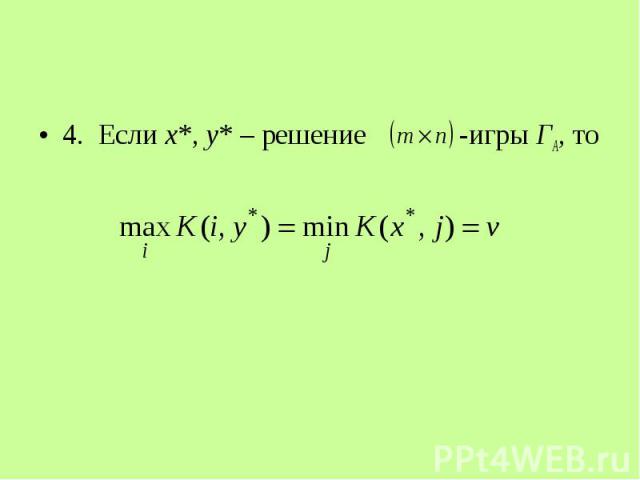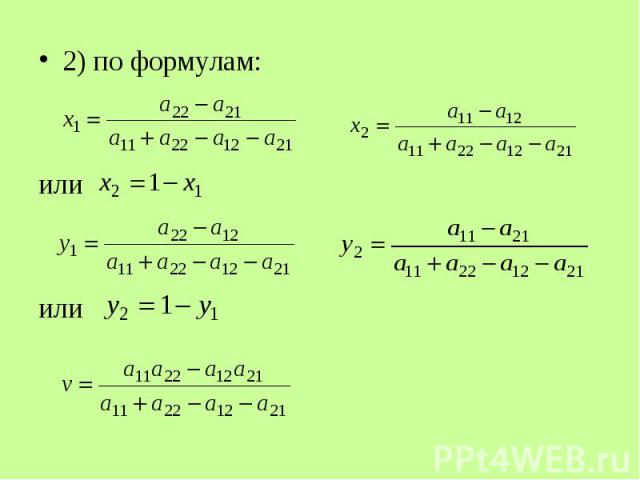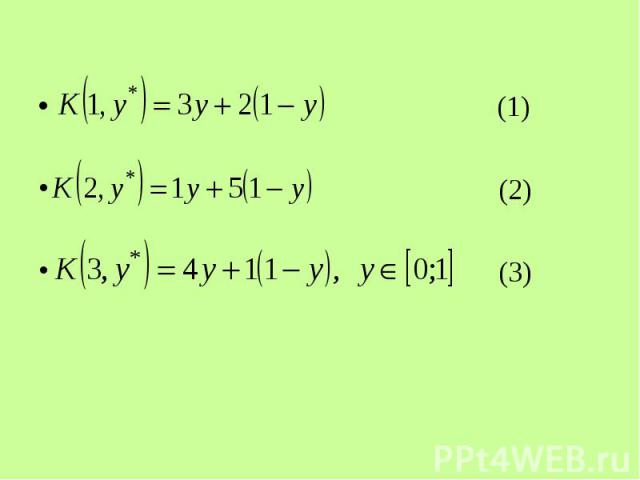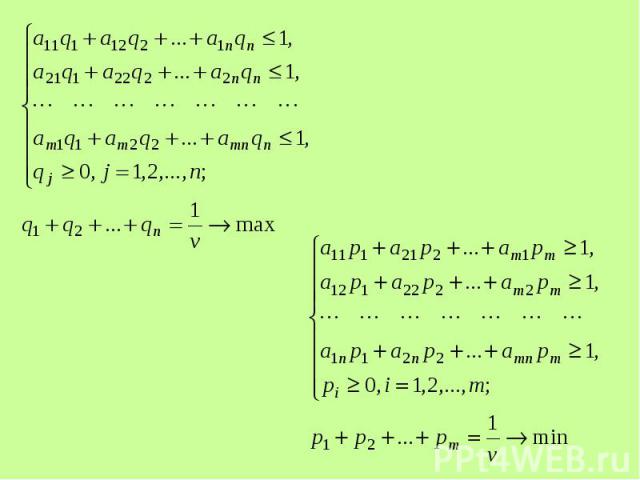Презентация на тему: ТЕОРИЯ ИГР

ТЕОРИЯ ИГР

Литература Петросян Л.А., Зенкевич Н.А., Семина Е.А. Теория игр. – М., 1998. 2. Воробьев Н.Н. Теория игр для экономистов-кибернетиков. – М.: Наука, 1985. 3. Дюбин Г.Н., Суздаль В.Г. Введение в прикладную теорию игр.– М.: Наука, 1981.

1. Основные понятия теории 1. Основные понятия теории матричных игр

Теория игр – это совокупность математических методов анализа и оценки конфликтных ситуаций. Теория игр – это совокупность математических методов анализа и оценки конфликтных ситуаций.

Содержание теории игр: Содержание теории игр: установление принципов оптимального поведения в условиях неопределенности (конфликта), доказательство существования решений, удовлетворяющих этим принципам, указание алгоритмов нахождения решений, их реализация.

Моделями теории игр можно описать экономические, правовые, классовые, военные конфликты, взаимодействие человека с природой. Моделями теории игр можно описать экономические, правовые, классовые, военные конфликты, взаимодействие человека с природой. Все такие модели в теории игр принято называть играми.

Игры можно классифицировать по различным признакам: Игры можно классифицировать по различным признакам: стратегические и чисто случайные, бескоалиционные и коалиционные, игры 1, 2, …, n лиц (по числу игроков), конечные и бесконечные (по числу стратегий), игры в нормальной форме и динамические, с нулевой суммой («антагонистические») и с ненулевой суммой.

Рассмотрим простейшую модель – игру, в которой участвуют два игрока, множество стратегий каждого игрока конечно, а выигрыш одного игрока равен проигрышу другого (бескоалиционная, конечная, антагонистическая игра двух лиц). Рассмотрим простейшую модель – игру, в которой участвуют два игрока, множество стратегий каждого игрока конечно, а выигрыш одного игрока равен проигрышу другого (бескоалиционная, конечная, антагонистическая игра двух лиц).

Такую игру (Г ) называют матричной. Такую игру (Г ) называют матричной. Она определяется тройкой Г=(X,Y,K), где Х – множество стратегий 1-го игрока, Y – множество стратегий 2-го игрока, K=K(x,y) – функция выигрыша (выигрыш 1-го игрока и соответственно проигрыш 2-го при условии, что 1-й игрок выбрал стратегию , а 2-й – стратегию ). Пару (x,y) называют ситуацией в игре Г.

Пусть 1-й игрок имеет всего m стратегий, а 2-й – n стратегий: Пусть 1-й игрок имеет всего m стратегий, а 2-й – n стратегий: Х=М={1,2, …, m}, Y=N={1,2, …, n}. Тогда игра Г полностью определяется заданием матрицы , где aij=K(i,j) – выигрыш 1-го игрока при условии, что он выбрал стратегию (т.е. строку) i, а 2-й игрок – стратегию (т.е. столбец) j (эти стратегии называют чистыми). Матрица А называется матрицей игры или платежной матрицей.

Пусть – платежная матрица игры Г. Пусть – платежная матрица игры Г. Если 1-й игрок выбрал стратегию i, то в худшем случае он выиграет . Поэтому он всегда может гарантировать себе выигрыш , обозначим его – нижняя цена игры, или максимин, соответствующая стратегия 1-го игрока называется максиминной.

Второй игрок, выбрав стратегию j, в худшем случае проиграет , а значит, может гарантировать себе проигрыш , Второй игрок, выбрав стратегию j, в худшем случае проиграет , а значит, может гарантировать себе проигрыш , обозначим его – верхняя цена игры, или минимакс, соответствующая стратегия 2-го игрока называется минимаксной.

Схема:

Например, Например, Соответствующие стратегии: i0=1(максиминная), j0=1,2 (минимаксная).

Справедливо неравенство: Справедливо неравенство:

Ситуация (i*, j*) называется ситуацией равновесия, или седловой точкой, если для любых , , выполняется неравенство Ситуация (i*, j*) называется ситуацией равновесия, или седловой точкой, если для любых , , выполняется неравенство Соответствующие стратегии i*, j* называются оптимальными чистыми стратегиями 1-го и 2-го игроков, а число называется ценой игры. Элемент является одновременно минимумом в своей строке и максимумом в своем столбце.

Ситуация равновесия существует тогда и только тогда, когда (это значение и является ценой игры v). Ситуация равновесия существует тогда и только тогда, когда (это значение и является ценой игры v).

Например, Например, (2,3)-ситуация равновесная, v =4 – цена игры, i*=2, j*=3 – оптимальные стратегии 1-го и 2-го игроков. Выбрав их, 1-й игрок обеспечит себе выигрыш не менее 4 ед., а 2-й игрок проиграет не более 4 ед. при любом выборе другого игрока.

Смешанной стратегией для 1-го игрока называется упорядоченная система m действительных чисел x=(x1, x2, …, xm), , Смешанной стратегией для 1-го игрока называется упорядоченная система m действительных чисел x=(x1, x2, …, xm), , , которые можно рассматривать как относительные частоты (вероятности), с которыми 1-й игрок выбирает чистые стратегии i=1, 2, …, m. Аналогично определяется смешанная стратегия для 2-го игрока: y=(y1, y2, …, yn), , .

Функция выигрыша K(x,y) в ситуации (x,y) определяется как математическое ожидание выигрыша 1-го игрока при условии, что 1-й и 2-й игроки выбрали соответственно стратегии x=(x1, x2, …, xm) и y=(y1, y2, …, yn): Функция выигрыша K(x,y) в ситуации (x,y) определяется как математическое ожидание выигрыша 1-го игрока при условии, что 1-й и 2-й игроки выбрали соответственно стратегии x=(x1, x2, …, xm) и y=(y1, y2, …, yn): .

Если для некоторых и и для всех и выполняется неравенство , то x*, y* называются оптимальными смешанными стратегиями игроков, Если для некоторых и и для всех и выполняется неравенство , то x*, y* называются оптимальными смешанными стратегиями игроков, число называется ценой игры, пара (x*, y*) – стратегической седловой точкой тройка x*, y*, v – решением игры.

Свойства оптимальных стратегий. Свойства оптимальных стратегий.

1. Пусть K(x,y) – математическое ожидание выигрыша в игре ГА с ценой v. 1. Пусть K(x,y) – математическое ожидание выигрыша в игре ГА с ценой v. Тогда, для того чтобы элемент был оптимальной стратегией 1-го игрока, необходимо и достаточно, чтобы для каждого элемента выполнялось неравенство Аналогично, для того чтобы был оптимальной стратегией 2-го игрока, необходимо и достаточно, чтобы для каждого выполнялось неравенство

2. Пусть K(x,y) – математическое ожидание выигрыша в игре ГА, 2. Пусть K(x,y) – математическое ожидание выигрыша в игре ГА, v – действительное число, , . Тогда, для того чтобы v было ценой игры, а x* и y* были оптимальными стратегиями соответственно 1-го и 2-го игроков, необходимо и достаточно, чтобы для любых и выполнялось неравенство

3. Пусть K(x,y) – математическое ожидание выигрыша в игре ГА с ценой v. 3. Пусть K(x,y) – математическое ожидание выигрыша в игре ГА с ценой v. Тогда, для того чтобы элемент был оптимальной стратегией 1-го игрока, необходимо и достаточно, чтобы для каждого выполнялось неравенство . Аналогично, для того чтобы был оптимальной стратегией 2-го игрока, необходимо и достаточно, чтобы для каждого выполнялось неравенство .

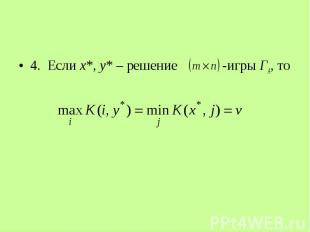
4. Если x*, y* – решение -игры ГА, то 4. Если x*, y* – решение -игры ГА, то

5. Пусть , , v – решение игры ГА. 5. Пусть , , v – решение игры ГА. Тогда для любого , при котором , выполняется неравенство xi=0, а для любого , при котором , выполняется неравенство yj=0.

6 (Лемма о масштабе). 6 (Лемма о масштабе). Если ГА – игра с матрицей , а – игра с матрицей , где , где α, =const, α>0, то множества оптимальных стратегий игроков в играх ГА и совпадают, а . Иначе говоря, две игры, отличающиеся лишь началом отсчета выигрышей и масштабом их измерения, стратегически эквивалентны.

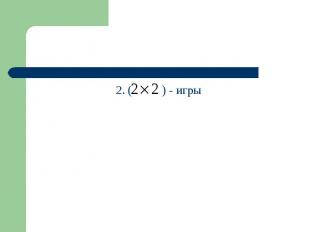
2. ( ) - игры 2. ( ) - игры

Пусть – платежная матрица игры Г. Если она не имеет седловой точки, то единственное решение игры Г можно найти

1) решив две системы: 1) решив две системы:

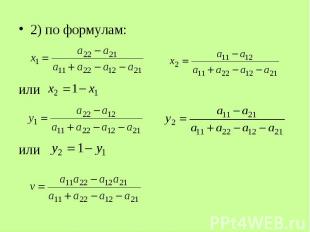
2) по формулам: 2) по формулам: или или

3) в матричном виде: 3) в матричном виде: где – определитель матрицы А, А* – присоединенная к А матрица, , , , JT и yT – транспонированные матрицы J и y.

Найдем, например, решение игры с Найдем, например, решение игры с платежной матрицей , которая не имеет седловой точки.

1) Составим системы: 1) Составим системы: Решив системы, получим: то есть -решение игры.

2) Найдем решение по формулам: 2) Найдем решение по формулам:

3) Найдем решение в матричном виде: 3) Найдем решение в матричном виде:

3. и – игры 3. и – игры

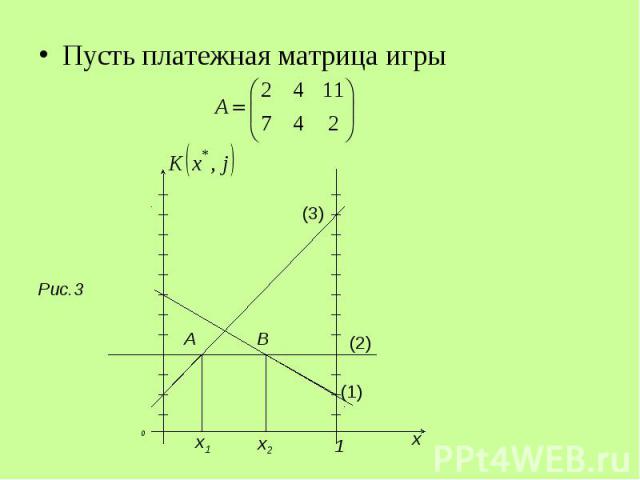
Рассмотрим игру с платежной матрицей Рассмотрим игру с платежной матрицей

Если 1-й игрок применит смешанную стратегию , а 2-й игрок – чистую стратегию , то Если 1-й игрок применит смешанную стратегию , а 2-й игрок – чистую стратегию , то .(1)

Аналогично при выборе 2-м игроком чистых стратегий , , Аналогично при выборе 2-м игроком чистых стратегий , , (2) (3) (4)

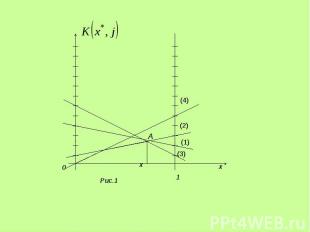
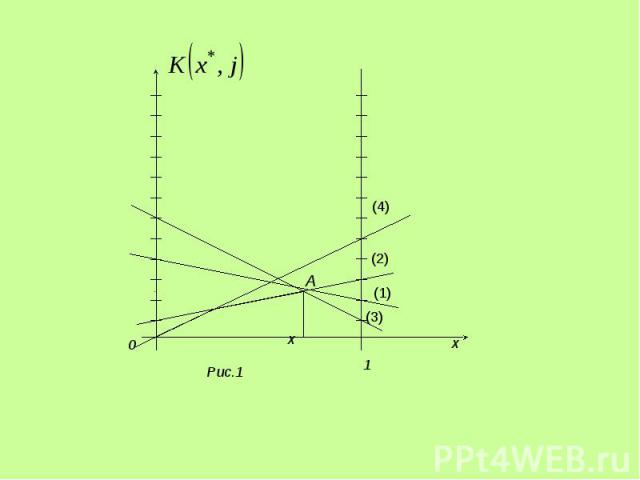
Точка A является точкой пересечения прямых (2) и (3), поэтому решение исходной игры можно найти, решив игру Точка A является точкой пересечения прямых (2) и (3), поэтому решение исходной игры можно найти, решив игру

По формулам решения – игры получим: По формулам решения – игры получим:

Тогда решение исходной игры имеет вид Тогда решение исходной игры имеет вид (номерам столбцов, не вошедших в матрицу , соответствуют нулевые координаты вектора ), .

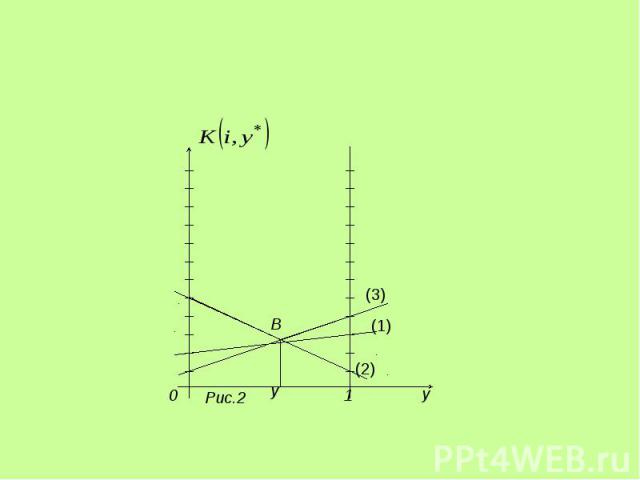
Аналогично решаются - игры. Аналогично решаются - игры. Пусть, например, , – смешанная стратегия 2-го игрока, 1-й игрок выбирает чистые стратегии i=1,2,3.

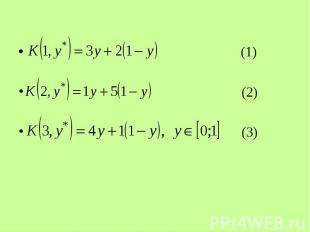
(1) (2) (3)

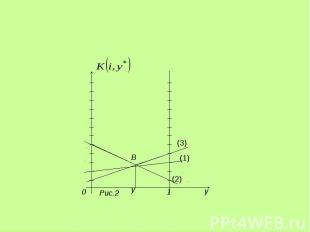
Точка B является точкой пересечения прямых (2) и (3). Найдем решение игры Точка B является точкой пересечения прямых (2) и (3). Найдем решение игры

Тогда решение исходной игры: Тогда решение исходной игры:

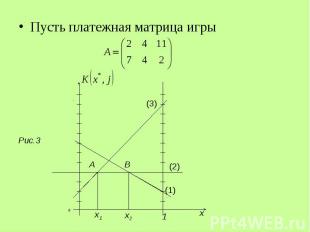
Пусть платежная матрица игры Пусть платежная матрица игры

A – точка пересечения прямых (2) и (3), ее абсциссу найдем, решая игру A – точка пересечения прямых (2) и (3), ее абсциссу найдем, решая игру

B – точка пересечения прямых (1) и (2), ее абсциссу найдем, решая игру B – точка пересечения прямых (1) и (2), ее абсциссу найдем, решая игру

Решение исходной игры: Решение исходной игры: , где , , то есть 1-й игрок имеет множество оптимальных стратегий, 2-й игрок – единственную оптимальную стратегию, это чистая стратегия j=2.

4. Доминирование стратегий 4. Доминирование стратегий

Иногда на основании простого рассмотрения матрицы игры можно сказать, что некоторые чистые стратегии могут войти в оптимальную смешанную стратегию лишь с нулевой вероятностью. Иногда на основании простого рассмотрения матрицы игры можно сказать, что некоторые чистые стратегии могут войти в оптимальную смешанную стратегию лишь с нулевой вероятностью.

В результате вместо игры ГА с матрицей А можно рассмотреть игру с матрицей

Легко найти решение игры Легко найти решение игры Можно предположить, что решение игры ГА будет иметь вид:

Говорят, что i-я стратегия 1-го игрока доминирует его k-ю стратегию, если для всех и хотя бы для одного j . Говорят, что i-я стратегия 1-го игрока доминирует его k-ю стратегию, если для всех и хотя бы для одного j . В этом случае говорят также, что i-я стратегия (или строка) – доминирующая, k-я – доминируемая.

Говорят, что j-я стратегия 2-го игрока доминирует его l-ю стратегию, если Говорят, что j-я стратегия 2-го игрока доминирует его l-ю стратегию, если для всех и хотя бы для одного i В этом случае j-ю стратегию (столбец) называют доминирующей, l-ю – доминируемой.

Стратегия может доминироваться также выпуклой линейной комбинацией других стратегий. Стратегия может доминироваться также выпуклой линейной комбинацией других стратегий. Так, i-я стратегия 1-го игрока доминируется выпуклой линейной комбинацией остальных стратегий, если ; j-я стратегия 2-го игрока доминируется выпуклой линейной комбинацией остальных стратегий, если

Если – некоторая смешанная стратегия, то ее расширением на i-ом месте будем называть стратегию вида Если – некоторая смешанная стратегия, то ее расширением на i-ом месте будем называть стратегию вида

теорема: пусть ГА – -игра, в которой i-я строка доминируема, – игра с матрицей , полученной из А вычеркиванием i-ой строки. Тогда теорема: пусть ГА – -игра, в которой i-я строка доминируема, – игра с матрицей , полученной из А вычеркиванием i-ой строки. Тогда 1) ; 2) всякая оптимальная стратегия 2-го игрока в игре является оптимальной и в игре ГА; 3) если x* – оптимальная стратегия 1-го игрока в игре , то – его оптимальная стратегия в игре ГА. Аналогичная теорема имеет место для доминируемого столбца.

5. Множество решений матричной игры 5. Множество решений матричной игры

Чтобы найти множество всех решений игры с платежной матрицей А, нужно рассмотреть все квадратные подматрицы матрицы А. Найдя решения игр, заданных подматрицами, нужно составить их расширения на соответствующих местах и проверить, являются ли полученные стратегии оптимальными для игры ГА.

Множество всех решений каждого игрока является выпуклой линейной комбинацией найденных решений. Множество всех решений каждого игрока является выпуклой линейной комбинацией найденных решений.

Решение игры, заданной квадратной подматрицей В, можно найти в матричном виде по формулам Решение игры, заданной квадратной подматрицей В, можно найти в матричном виде по формулам

Найдем, например, множество всех решений игры ГА с платежной матрицей Найдем, например, множество всех решений игры ГА с платежной матрицей

Подматрицы не дадут решений, так как матрица А не имеет седловых точек. Рассмотрим подматрицы : Подматрицы не дадут решений, так как матрица А не имеет седловых точек. Рассмотрим подматрицы :

Для В: является решением игры ГА (убеждаемся в этом проверкой). Для В: является решением игры ГА (убеждаемся в этом проверкой).

Для С: Для С: – является решением игры ГА. Для D получим такое же решение, как для В.

Таким образом, в игре ГА 1-й игрок имеет единственную оптимальную стратегию Таким образом, в игре ГА 1-й игрок имеет единственную оптимальную стратегию 2-й игрок имеет множество оптимальных стратегий где , , цена игры v=1.

6. Сведение матричной игры к двойственной задаче линейного программирования 6. Сведение матричной игры к двойственной задаче линейного программирования

Пусть матрица игры имеет вид Пусть матрица игры имеет вид K=K(x,y)– функция выигрыша, , , .

Тогда по свойству 2 оптимальных стратегий для любых , должно выполняться условие Тогда по свойству 2 оптимальных стратегий для любых , должно выполняться условие

То есть То есть

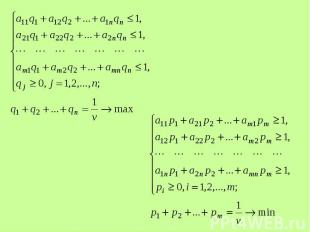
Пример. Найти решение игры с матрицей Пример. Найти решение игры с матрицей

Решение. Перейдем к положительной матрице, прибавив 3 ко всем элементам матрицы А: Решение. Перейдем к положительной матрице, прибавив 3 ко всем элементам матрицы А:

Составим двойственную задачу линейного программирования: Составим двойственную задачу линейного программирования:

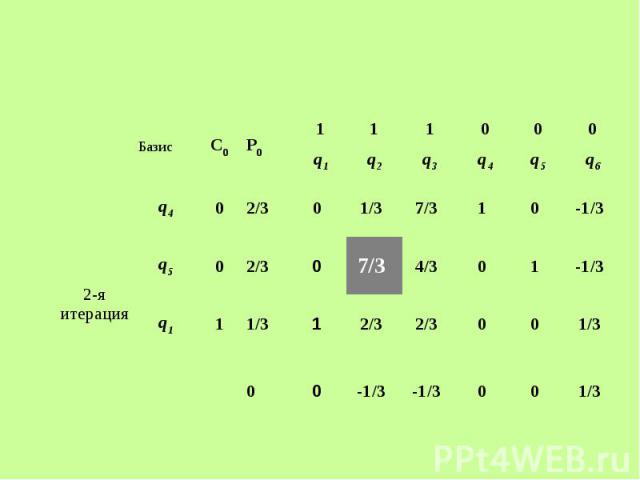
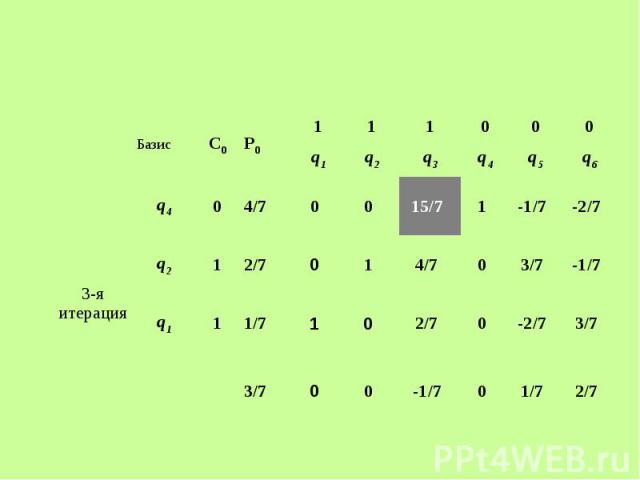
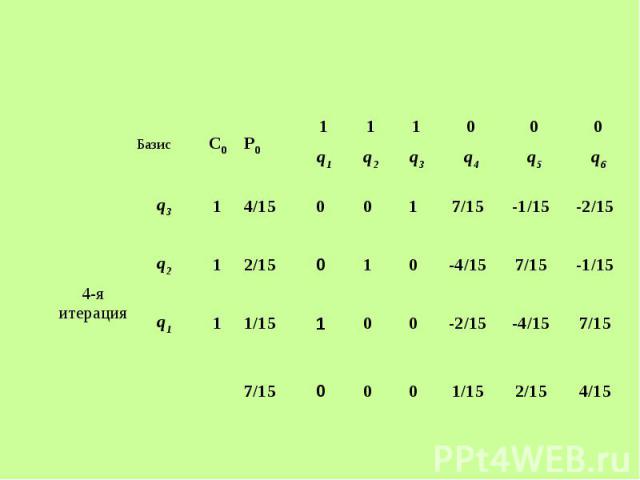
Решим задачу симплексным методом Решим задачу симплексным методом

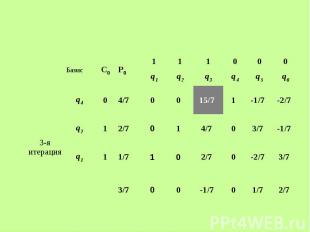
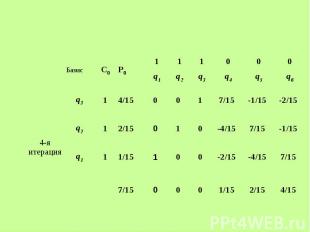
Получаем решение двойственной задачи: Получаем решение двойственной задачи:

Тогда решение игры с матрицей Тогда решение игры с матрицей Решение исходной игры:

7. Приближенное решение матричных игр 7. Приближенное решение матричных игр

где v – цена игры, где v – цена игры, k– номер партии, – максимальное значение суммарного выигрыша 1-го игрока в k-ой партии при выборе различных стратегий, – минимальное значение суммарного проигрыша 2-го игрока в k-ой партии при выборе различных стратегий.

За приближенные оптимальные стратегии игроков принимают векторы, координатами которых являются относительные частоты выбора соответствующих чистых стратегий. За приближенные оптимальные стратегии игроков принимают векторы, координатами которых являются относительные частоты выбора соответствующих чистых стратегий.

Пример. Найти приближенное решение игры, заданной матрицей Пример. Найти приближенное решение игры, заданной матрицей

Приближенное решение игры за 12 партий: v =1,45,