Презентация на тему: СИММЕТРИЯ И ДВИЖЕНИЕ (9 КЛАСС)

Со времён Пифагора известны они. Со времён Пифагора известны они. В них равные стороны и равны углы. Их встретим в орнаментах и на паркетах В стихотворениях разных поэтов. И даже пчёлы с ними работают, Строя в их форме домики-соты. О. Панишева.

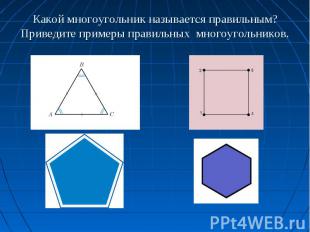
Какой многоугольник называется правильным? Приведите примеры правильных многоугольников.

Как найти сумму углов правильного многоугольника ? Как найти градусную величину внутреннего угла правильного выпуклого многоугольника?

Задача №1 Во дворе нашей школы есть клумба квадратной формы. Весной мы будем высаживать цветы на нашу клумбу. Сначала высаживать будем ландыши по окружности, которую можно вписать в квадратную клумбу. Затем тюльпаны в форме квадрата, вписанного в окружность. Сколько саженцев ландышей и клубней тюльпанов нужно высадить, если размеры клумбы 6х6 квадратных метров. Воспользоваться значением , . Высаживать цветы нужно через каждые 20 см.

Задача №2 Пчелиные соты представляют собой прямоугольник, покрытый правильными шестиугольниками. Найти, какими ещё правильными многоугольниками можно покрыть плоскость. Что для этого нужно знать?

n=3. Три угла, плотно составленные, составляют 180°, шесть углов - 360°. Плоскость покрыта без просветов. n=3. Три угла, плотно составленные, составляют 180°, шесть углов - 360°. Плоскость покрыта без просветов. n=4. Четыре внутренних угла вместе дают 360°, плоскость покрыта без просветов. n=5. Внутренний угол правильного многоугольника равен 108°, остаётся просвет в 36°. Плоскость без просветов не покрывается. n=6. Внутренний угол правильного шестиугольника равен 120°, три шестиугольника, составленные вместе, образуют 360°. Плоскость покрывается без просветов. Метод перебора можно продолжать и дальше, итогом будет служить вывод, чтобы без просветов плоскость можно покрыть лишь правильными треугольниками, квадратами, правильными шестиугольниками.

Почему пчёлы выбрали именно шестиугольник?

Для ответа на этот вопрос нужно сравнить периметры разных многоугольников, имеющих одинаковую площадь. Пусть даны правильный треугольник, квадрат и правильный шестиугольник. У какого из этих многоугольников наименьший периметр? Для ответа на этот вопрос нужно сравнить периметры разных многоугольников, имеющих одинаковую площадь. Пусть даны правильный треугольник, квадрат и правильный шестиугольник. У какого из этих многоугольников наименьший периметр? Пусть S- площадь каждой из названных фигур, сторона аn- соответствующего правильного n-угольника. Для сравнения периметров запишем их соотношение Р3 : Р4 : Р6 = 1 : 0,877 : 0,816 Мы видим, что из трёх правильных многоугольников с одинаковой площадью наименьший периметр имеет правильный шестиугольник. Стало быть, мудрые пчёлы, экономят воск и время для построения сот.

На этом математические секреты пчёл не заканчиваются. Интересно и дальше исследовать строение пчелиных сот. Расчётливые пчёлы заполняют пространство так, что не остаётся просветов, экономя при этом 2% воска. Как не согласиться с мнением Пчелы из сказки «Тысяча и одна ночь»: «Мой дом построен по законам самой строгой архитектуры. Сам Евклид мог бы поучиться, познавая геометрию моих сот». Так с помощью геометрии мы прикоснулись к тайне математических шедевров из воска, ещё раз убедившись во всесторонней эффективности математики. На этом математические секреты пчёл не заканчиваются. Интересно и дальше исследовать строение пчелиных сот. Расчётливые пчёлы заполняют пространство так, что не остаётся просветов, экономя при этом 2% воска. Как не согласиться с мнением Пчелы из сказки «Тысяча и одна ночь»: «Мой дом построен по законам самой строгой архитектуры. Сам Евклид мог бы поучиться, познавая геометрию моих сот». Так с помощью геометрии мы прикоснулись к тайне математических шедевров из воска, ещё раз убедившись во всесторонней эффективности математики.

Задача №3. Пол комнаты, имеющий форму прямоугольника со сторонами 5,5 м и 6 м, нужно покрыть паркетом прямоугольной формы. Длина каждой дощечки паркета равна 30 см, а ширина — 5 см. Сколько потребуется таких дощечек для покрытия пола?

Рефлексия: Что нового вы сегодня для себя узнали? Чему научились? Что давалось легко, а что вызывало затруднения? Где вы будете использовать данные ЗУНы? Какой информации было недостаточно при выполнении тех или иных заданий? Над чем стоит еще поработать дома?