Презентация на тему: Решение задач на нахождение площади

Решение задач на нахождение площади МОУ ООШ с.Ст.ТурдакиДемидова Людмила Анатольевна
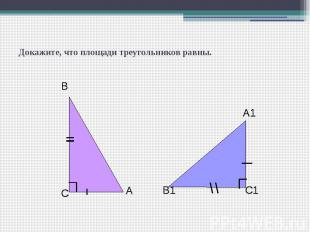
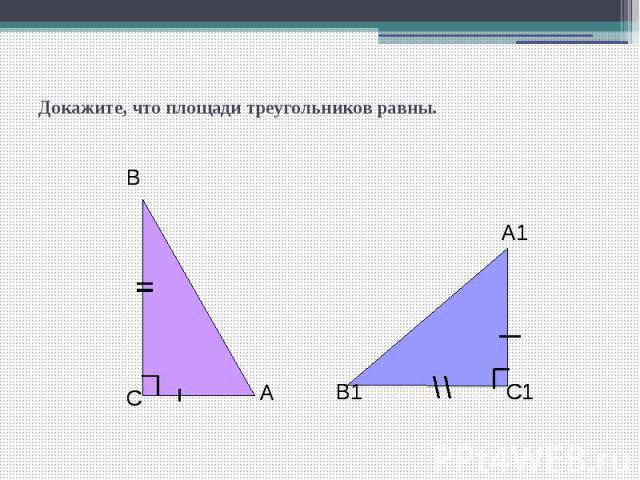
Докажите, что площади треугольников равны.
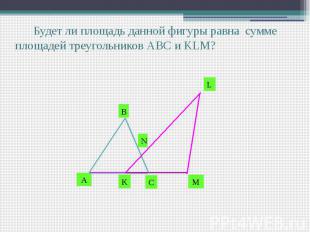
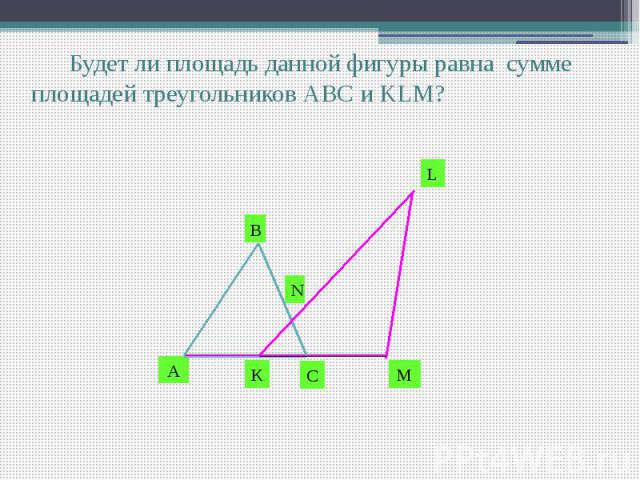
Будет ли площадь данной фигуры равна сумме площадей треугольников АВС и KLM?

Свойства площадей многоугольников Равные многоугольники имеют равные площади.Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.

Повторим формулы площадей Sквадрата = а·а = а² Sквадрата =0,5 d² S = а·b
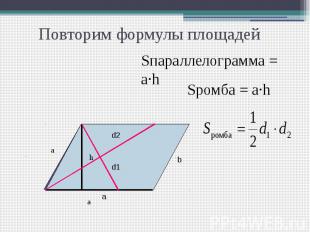
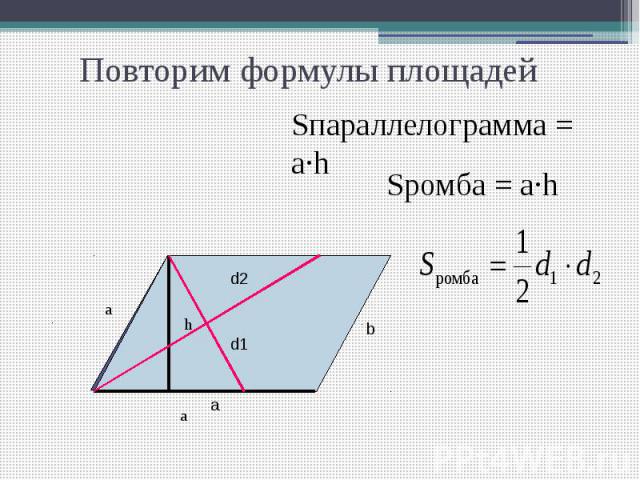
Повторим формулы площадей Sпараллелограмма = а·h Sромба = а·h

Повторим формулы площадей

Теорема Пифагора В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. c²=a²+b² Теорема, обратная теореме Пифагора: если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный.
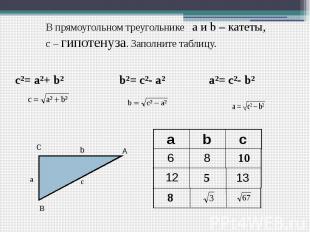
В прямоугольном треугольнике а и b – катеты, с – гипотенуза. Заполните таблицу. c²= a²+ b² b²= c²- a² a²= c²- b²
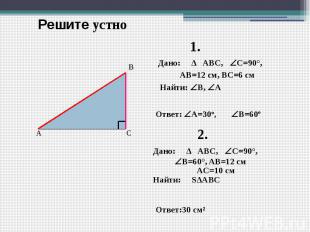
Решите устно Дано: ∆ ABC, C=90°, AB=12 см, ВC=6 см Найти: B, А Ответ: А=30º, Дано: ∆ ABC, C=90°, B=60°, AB=12 см AC=10 см Найти: S∆АВС

Диагонали ромба равны 12 см и 16 см.Найдите сторону и площадь ромба. ∆ABO – прямоугольный, найдем АВ по теореме Пифагора: АВ²=ВО²+АО² АВ=10 (см) Ответ: 10 см и 96 см².
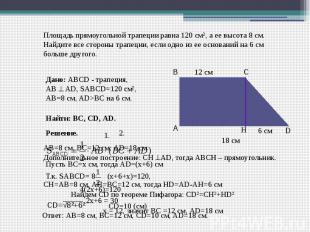
Площадь прямоугольной трапеции равна 120 см², а ее высота 8 см. Найдите все стороны трапеции, если одно из ее оснований на 6 см больше другого. Дано: ABCD - трапеция, АВ AD, SАВСD=120 см², АВ=8 см, AD>BC на 6 см.
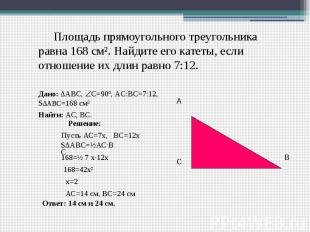
Площадь прямоугольного треугольникаравна 168 см². Найдите его катеты, если отношение их длин равно 7:12. Дано: ∆ABC, С=90º, АC:ВС=7:12, S∆ABC=168 см² Найти: АС, BС.

Домашнее задание№517, 504