Презентация на тему: Работа с КИМ-2010

Урок- повторение: «Работа с КИМ-2010»

«Величие человека – в его способности мыслить.» Б. Паскаль

Устно.3х = 7; 2х = 32;
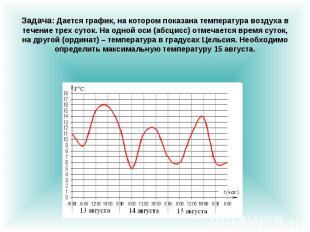
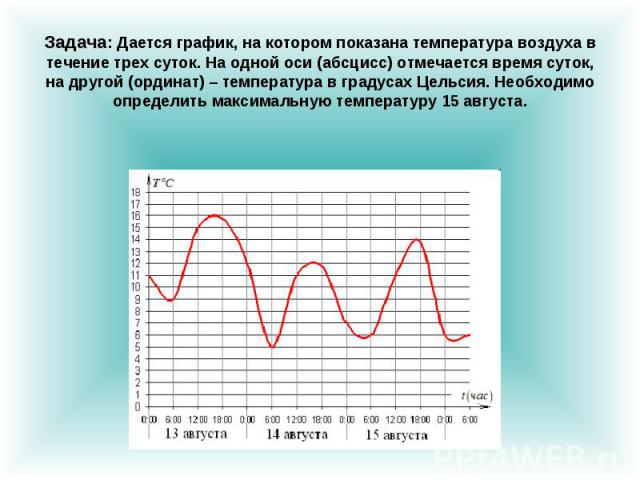
Задача: Дается график, на котором показана температура воздуха в течение трех суток. На одной оси (абсцисс) отмечается время суток, на другой (ординат) – температура в градусах Цельсия. Необходимо определить максимальную температуру 15 августа.
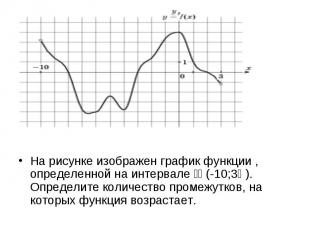
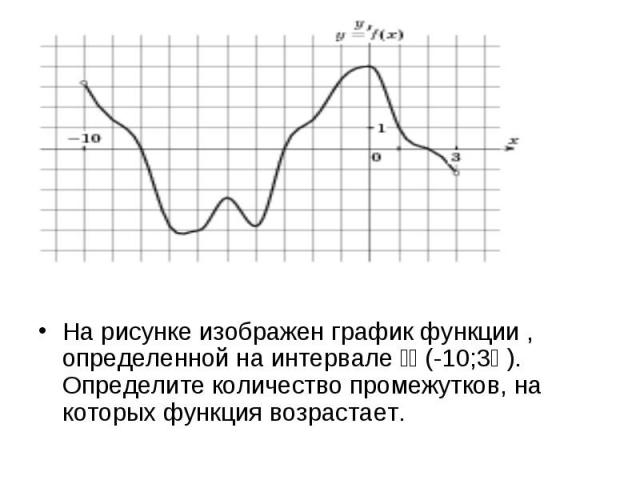
На рисунке изображен график функции , определенной на интервале (-10;3 ). Определите количество промежутков, на которых функция возрастает.
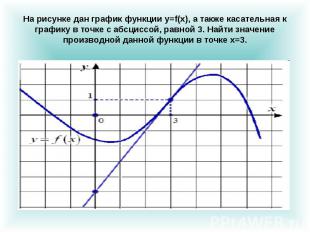
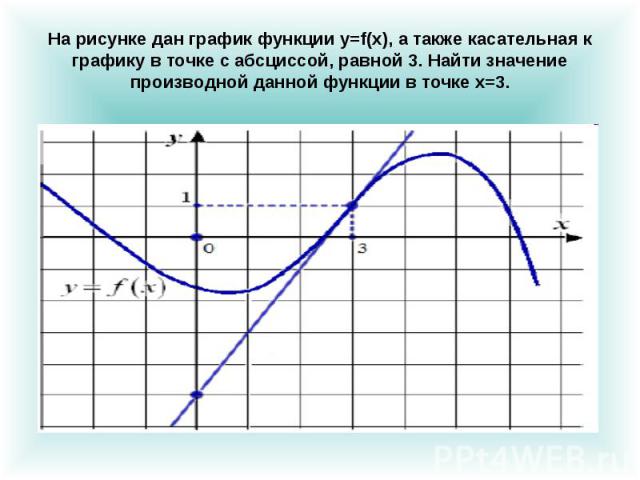
На рисунке дан график функции y=f(x), а также касательная к графику в точке с абсциссой, равной 3. Найти значение производной данной функции в точке х=3.
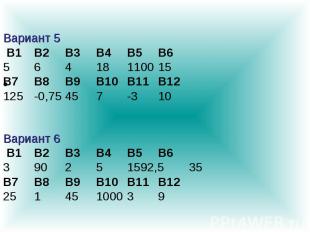
Вариант 5 В1 В2 В3 В4 В5 В6 5 6 4 18 1100 15 В7 В8 В9 В10 В11 В12 125 -0,75 45 7 -3 10 Вариант 6 В1 В2 В3 В4 В5 В6 3 90 2 5 1592,5 35 В7 В8 В9 В10 В11 В12 25 1 45 1000 3 9

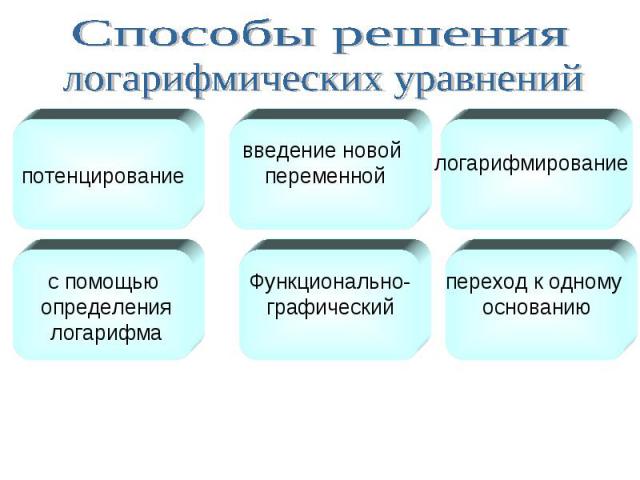
Способы решения логарифмических уравнений
Способы решениялогарифмических уравнений

Метод потенцирования Он основан на теореме равносильности.Теорема: Пусть а>0 и а =1, x- решение системы неравенства f (x)>0, g (x)>0,Тогда уравнение logaf(x)=logag(x) на множестве x уравнению f(x)=g(x)

Метод введения новой переменной

Решение логарифмических уравнений на основании определения логарифма2.f(x)=ab (по определению логарифма)3.отбор корней, удовлетворяющих ОДЗ.

Функционально-графический методРешая уравнение f(x)=g(x):Нужно построить график функции у =f (x) ,y=g(x) и найти точки их пересечения. Корнями служат абсциссы этих точек. log2x=3-xВ некоторых случаях построение графиков функций можно заменить ссылкой на свойства функций:Если одна из функций у =f(х) или у =g(х) возрастает, а другая убывает на промежутке Х,то уравнение g(х)= f(х) имеет не более одного корня.

Метод приведение логарифмов к одному основаниюФормулы перехода к новому основанию

Свойства логарифмов

Иррациональные уравнения

ОпределениеУравнения содержащие переменную под знаком корня, называются иррациональными уравнениямиСпособы решенияВозведение обеих частей уравнения в степеньНахождение области допустимых значений неизвестного Использование равносильных переходов

Возведение обеих частей уравнения в степеньПри возведении обеих частей уравнения в четную степень могут появиться посторонние корни. Поэтому при использовании указанного метода следует проверить все найденные корни подстановкой в исходное уравнение.

2. Нахождение области допустимых значенийПереносим выражение, содержащее квадратный корень в левую частьПоскольку корни арифметические, то левая часть уравнения неотрицательна, а правая отрицательна. Значит, уравнение решений не имеет