Презентация на тему: Обозначения натуральных чисел

Обозначения натуральных чисел. Для счета предметов применяют натуральные числа. Любое натуральное число можно записать с помощью десяти цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Такая запись чисел называется десятичной. Натуральный ряд – последовательность всех натуральных чисел: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, …. Свойства натурального ряда: Самое маленькое число – 1 (единица) Каждое следующее число натурального ряда на 1 больше предыдущего. Натуральный ряд бесконечен, наибольшего числа в нем нет.

Обозначения натуральных чисел. Значение цифры зависит от её места в записи числа: Пример: 12584 - Цифра 4 в разряде единиц 346 - цифра 4 в разряде десятков 7480 - цифра 4 в разряде сотен Цифра «0» – нуль – обозначение отсутствия единиц, ни одной. «0» – нуль не натуральное число.

Обозначения натуральных чисел. Если запись натурального числа состоит из одного знака – цифры, то его называют однозначным: 5 – однозначное число 7 – однозначное число 12 – двузначное число 14 – двузначное число 528 – трехзначное число 864 – трехзначное число 1 261 – четырехзначное число 4 629 – четырехзначное число 58 421 – пятизначное число 148 735 – шестизначное число Двухзначные, трехзначные, четырехзначные и т.д. числа называют многозначными.

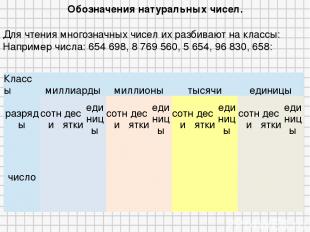
Обозначения натуральных чисел. Для чтения многозначных чисел их разбивают на классы: Например числа: 654 698, 8 769 560, 5 654, 96 830, 658: Классы миллиарды миллионы тысячи единицы разряды сотни десятки единицы сотни десятки единицы сотни десятки единицы сотни десятки единицы число                                                                                                                        

Обозначения натуральных чисел. Решение задач. № 1, 2(а, в, д), 3(а-д), 18, 19, 22(а-д) Домашнее задание: № 2(б, г, е), 3(е-к), 20