Презентация на тему: ГИА 2013 Модуль «АЛГЕБРА» №4

ГИА 2013Модуль «АЛГЕБРА»№4Автор презентации: Гладунец Ирина Владимировнаучитель математики МБОУ гимназии №1 г.Лебедянь Липецкой области

Модуль «Алгебра» №4

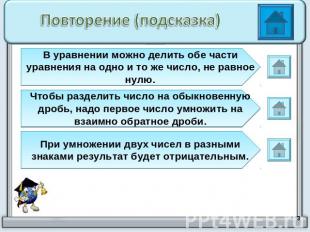
Повторение (подсказка)В уравнении можно делить обе части уравнения на одно и то же число, не равное нулю.Чтобы разделить число на обыкновенную дробь, надо первое число умножить на взаимно обратное дроби.При умножении двух чисел в разными знаками результат будет отрицательным.

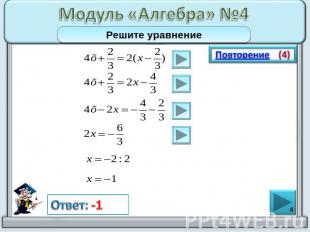
Модуль «Алгебра» №4

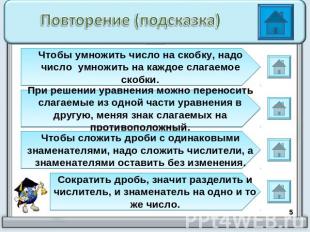
Повторение (подсказка)Чтобы умножить число на скобку, надо число умножить на каждое слагаемое скобки.При решении уравнения можно переносить слагаемые из одной части уравнения в другую, меняя знак слагаемых на противоположный.Чтобы сложить дроби с одинаковыми знаменателями, надо сложить числители, а знаменателями оставить без изменения.Сократить дробь, значит разделить и числитель, и знаменатель на одно и то же число.

Модуль «Алгебра» №4

Повторение (подсказка)Чтобы умножить одночлен на многочлен, надо одночлен умножить на каждый член многочлена.Чтобы сложить (вычесть) дроби с разными знаменателями, надо привести дроби к общему знаменателю и сложить (вычесть) числители.Чтобы умножить обыкновенные дроби, надо перемножить отдельно числители и знаменатели.Чтобы выделить целую часть из неправильной дроби, надо числитель разделить на знаменатель, неполное частное – целая часть, остаток – числитель, знаменатель без изменения

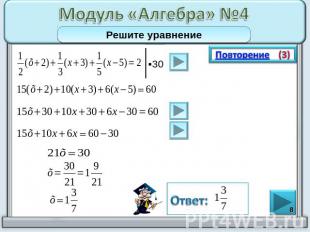
Модуль «Алгебра» №4

Повторение (подсказка)Чтобы «избавиться» от дробей, надо уравнение почленно умножить на общий знаменатель дробей, входящих в уравнение.Сумма противоположных чисел равна нулю.Подобными слагаемыми называются те, которые имеют одинаковую буквенную часть или не имеют ее вовсе.

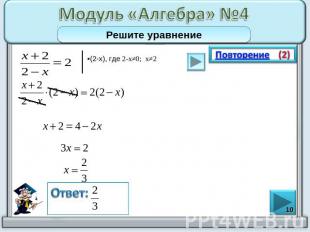
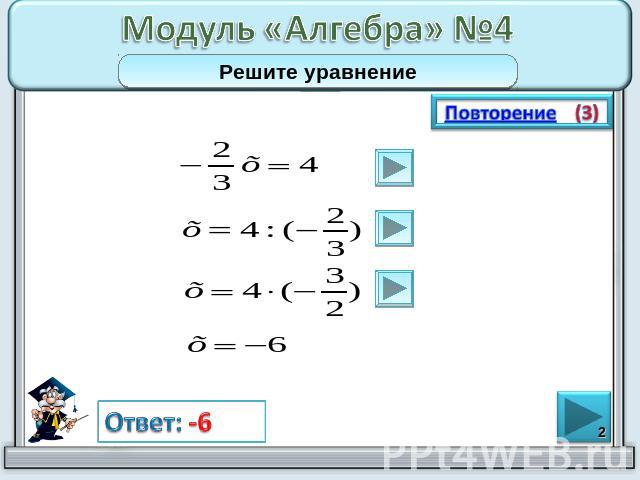
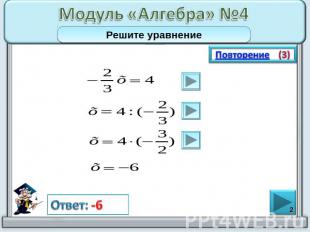
Модуль «Алгебра» №4Решите уравнение

Повторение (подсказка)Дробно-рациональное уравнение имеет смысл тогда, когда знаменатель дробей, входящих в уравнение, не равен нулю.Дробно-рациональное уравнение можно свести к целому, если обе его части умножить на общий знаменатель.

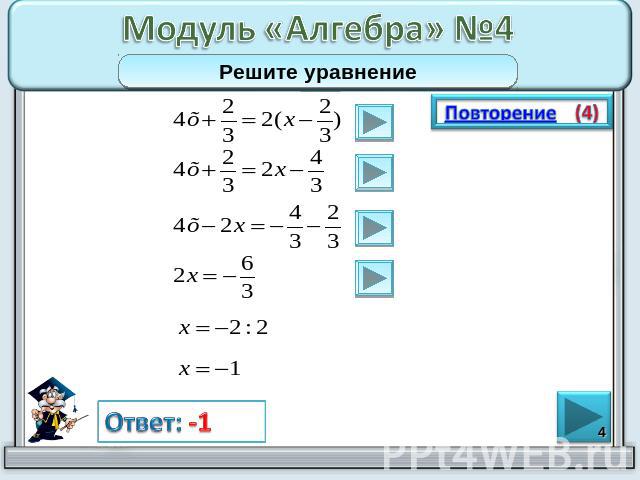
Модуль «Алгебра» №4Решите уравнение

Повторение (подсказка)В верной пропорции произведение крайних членов равно произведению средних членов.Собираем подобные слагаемые, т.е. переносим их из одной части уравнения в другую, меняя их знаки на противоположные.Если сложить числа с противоположными знаками, то надо из большего модуля вычесть меньший, поставив в ответе знак числа с большим модулем.

Модуль «Алгебра» №4

Повторение (подсказка)Квадратным уравнением называется уравнение вида ax²+bx+c=0Дискриминант – различитель можно найти по формулеТак как D>0, то уравнение имеет два корня.Корни квадратного уравнения можно вычислить по формулам:

Модуль «Алгебра» №4

Повторение (подсказка)Если все числовые коэффициенты уравнения имеют общий делитель, то их можно сократить на этот делитель.Приведенным называется квадратное уравнение, старший коэффициент которого равен единице.Если числа х₁ и х₂ таковы, что х₁+х₂=-b, х₁∙х₂=с, то эти числа – корни уравнения (обратная теорема Виета).

Решим систему методом подстановки:Решим систему методом подстановки:Модуль «Алгебра» №4Решим систему методом подстановки:

Повторение (подсказка)Чтобы решить систему уравнений методом подстановки, надо вместо у во втором уравнении подставить 2х, и получим уравнение с одной переменной.Чтобы найти значение второй переменной (у), надо в первое уравнение подставить вместо х значение равное 2 и решить получившееся уравнение.Решение системы уравнений записывают парой чисел в виде координат точки.

Модуль «Алгебра» №4

Если пред скобкой стоит знак «минус», то при раскрытии скобок скобки и этот знак опускают, а знаки в скобках меняют на противоположные.Умножить почленно каждое уравнение на такие множители, чтобы при одной из переменных получить противоположные коэффициенты.Надо сложить почленно уравнения чтобы исключить одну из переменных (в данном случае х), и решить получившееся уравнение с одной переменной. Если одно из уравнений не имеет решения, то и система не имеет решения.

http://krasdo.ucoz.ru/ee383358c499.png http://krasdo.ucoz.ru/ee383358c499.png http://www.grafamania.net/uploads/posts/2008-08/1219611582_7.jpg Автор данного шаблона Ермолаева Ирина Алексеевна - учитель информатики и ИКТ (Муниципальное общеобразовательное учреждение «Павловская средняя общеобразовательная школа») http://narod.ru/disk/20305179001/SHabloni 2.rar.html«ГИА-2013. Математика: типовые экзаменационные варианты: 30 вариантов» под редакцией А. Л. Семенова, И. В. Ященко. – М.: Изд. «Национальное образование», 2013.