Презентация на тему: ГИА 2013. Модуль «АЛГЕБРА» №7

ГИА 2013.Модуль «АЛГЕБРА»№7Автор презентации: Гладунец Ирина Владимировнаучитель математики МБОУ гимназии №1 г.Лебедянь Липецкой области

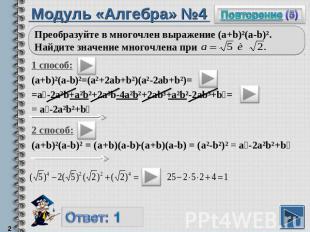
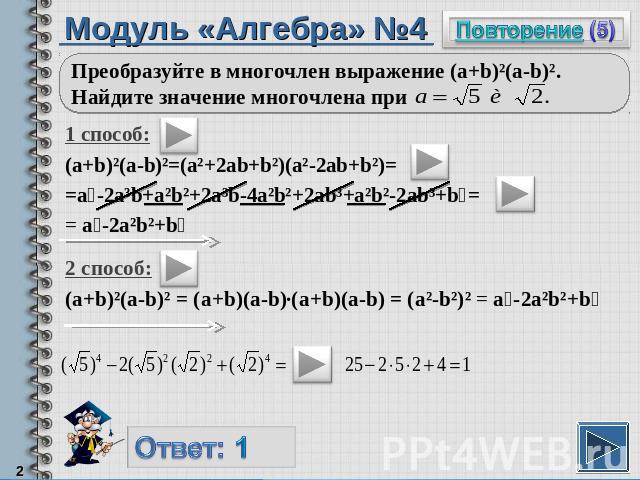
Модуль «Алгебра» №4Преобразуйте в многочлен выражение (a+b)²(a-b)². Найдите значение многочлена при 1 способ:(a+b)²(a-b)²=(a²+2ab+b²)(a²-2ab+b²)==a⁴-2a³b+a²b²+2a³b-4a²b²+2ab³+a²b²-2ab³+b⁴== a⁴-2a²b²+b⁴2 способ:(a+b)²(a-b)² = (a+b)(a-b)∙(a+b)(a-b) = (a²-b²)² = a⁴-2a²b²+b⁴

Повторение (подсказка)Квадрат суммы (разности) двух выражений равен квадрату первого выражения плюс (минус) удвоенное произведение первого и второго выражений и плюс квадрат второго выражения.Чтобы умножить многочлен на многочлен, надо умножить каждый член одного Если у слагаемых одинаковая буквенная часть, то они подобны. При сложении таких слагаемых складывают коэффициенты и умножают на общую буквенную часть.Произведение разности двух выражений на их сумму равно разности квадратов этих выражений.

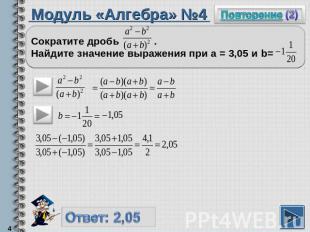
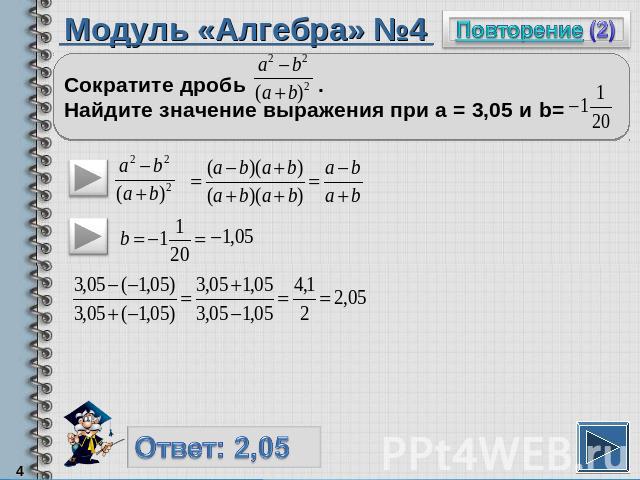
Модуль «Алгебра» №4Сократите дробь . Найдите значение выражения при а = 3,05 и b=

Повторение (подсказка)Чтобы сократить дробь, надо и числитель, и знаменатель разложить на множители.Чтобы перевести обыкновенную дробь в десятичную, надо числитель разделить на знаменатель.

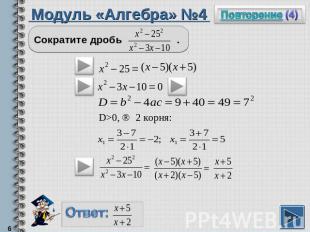
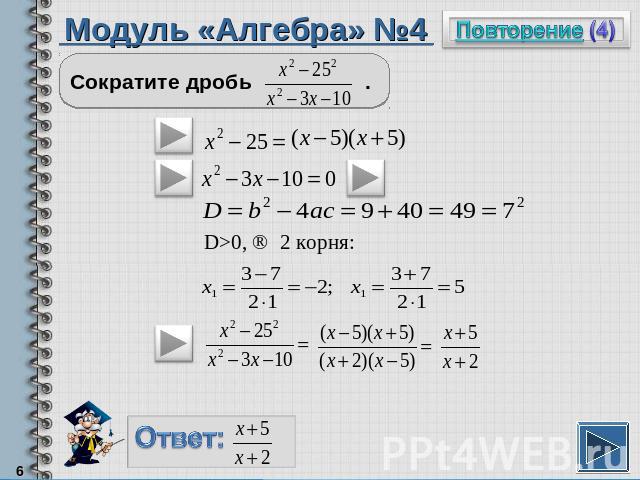
Модуль «Алгебра» №4Сократите дробь .

Повторение (подсказка)Разность квадратов равна произведению разности этих выражений на из сумму.Квадратный трехчлен можно разложить на множители по формуле Корни квадратного трехчлена можно найти по формулам:Чтобы сократить дробь, надо и числитель и знаменатель разделить на одно и тоже выражение, не равное нулю.

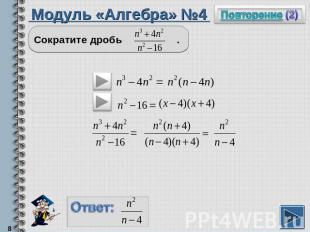
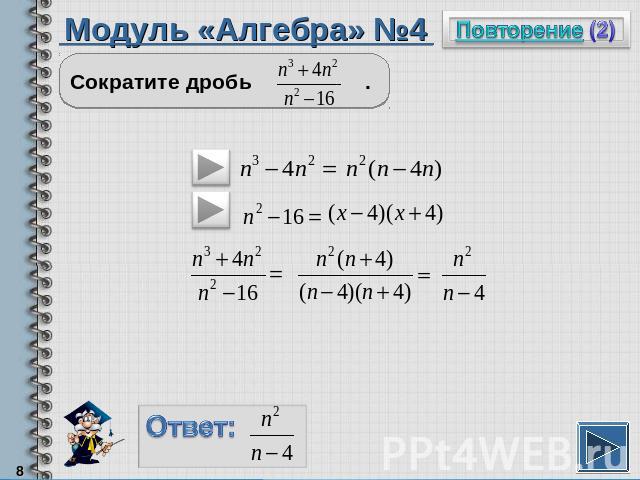
Модуль «Алгебра» №4Сократите дробь .

Повторение (подсказка)Если у слагаемых есть общий множитель, то при разложении многочлена на множители этот множитель можно вынести за скобку.Разность квадратов можно разложить по формуле:

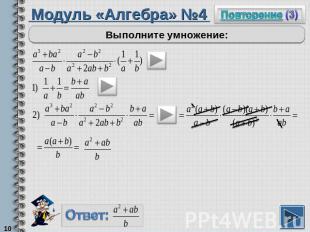
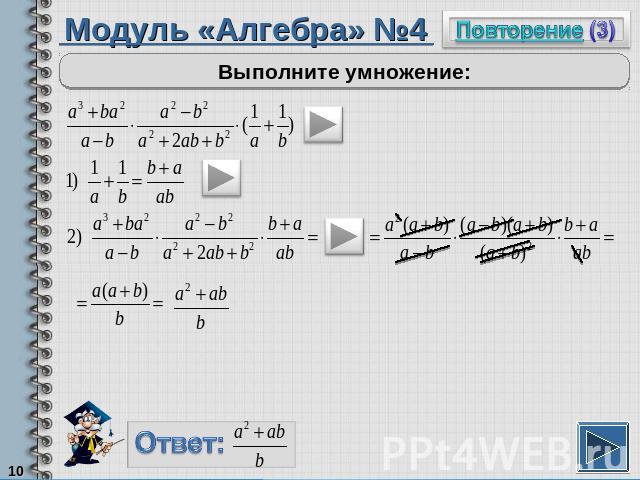
Модуль «Алгебра» №4Выполните умножение:

Повторение (подсказка)Чтобы сложить дроби с разными знаменателями, надо привести дроби к общему знаменателю и сложить числитЧтобы умножить дроби, надо отдельно умножить числители и знаменатели.В процессе умножения дробей можно сокращать. Для этого надо числители и знаменатели дробей разложить на множителиТрехчлен a²+2ab+b² можно «свернуть» по формуле

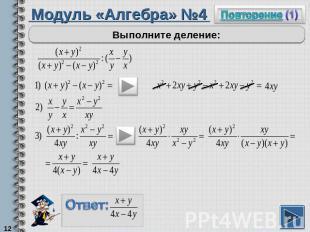
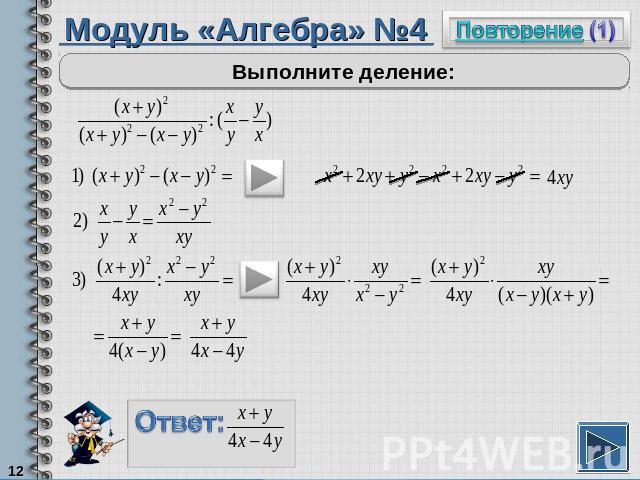
Модуль «Алгебра» №4Выполните деление:

Повторение (подсказка)Сумма противоположных слагаемых равна нулю.Чтобы разделить дробь на дробь, надо первую дробь умножить на обратную второй дроби.

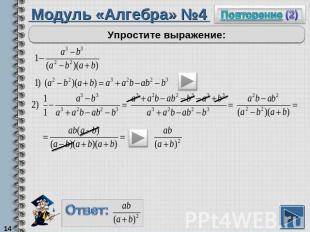
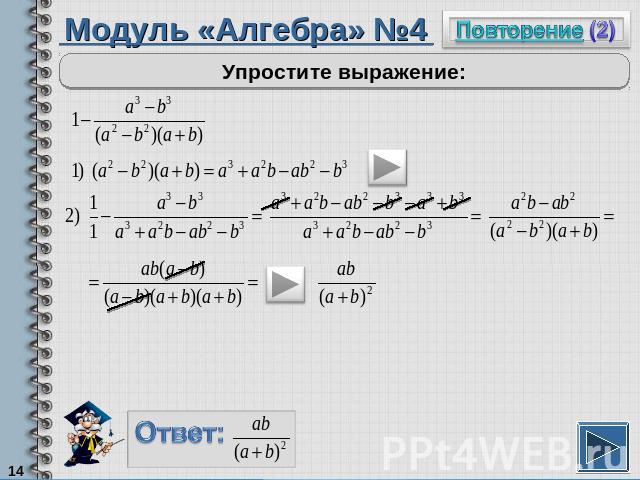
Модуль «Алгебра» №4Упростите выражение:

Чтобы сложить с дробью натуральное число, надо это число представить в виде дроби со знаменателем 1 и сложить по правилу дробей.Произведение двух одинаковых множителей можно записать в виде квадрата этого множителя.

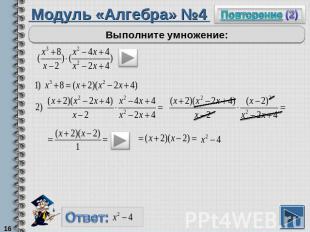
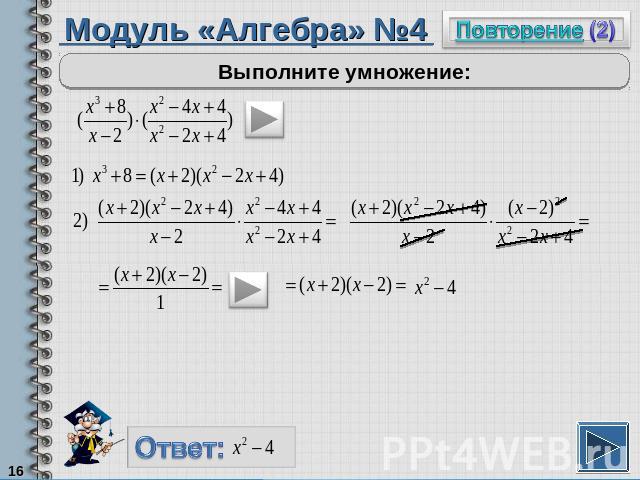
Модуль «Алгебра» №4Выполните умножение:

Повторение (подсказка)Сумму кубов двух выражений можно разложить по формулеДробь, знаменатель которой равен единице, является целым выражением.

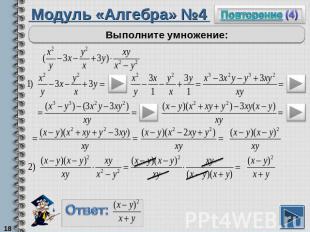
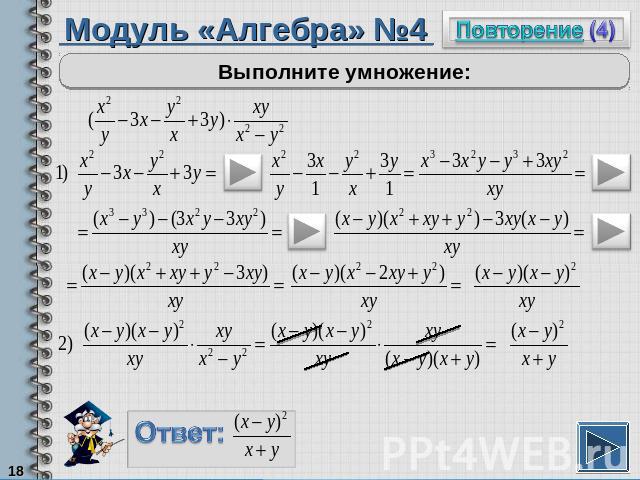
Модуль «Алгебра» №4Выполните умножение:

Повторение (подсказка)Чтобы сложить дробь с одночленом, надо одночлен заменить дробью со знаменателем 1 и выполнить сложение дробей.Чтобы разложить многочлен на множители (в случае, если формулы сокращенного умножения на подходят), можно применить способ группировки.Далее надо каждую скобку разложить на множители своим способом.Далее общий множитель в виде многочлена вынести за скобку.

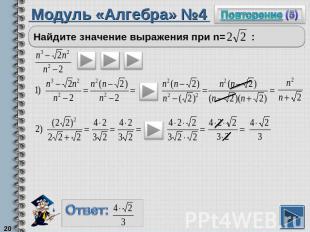
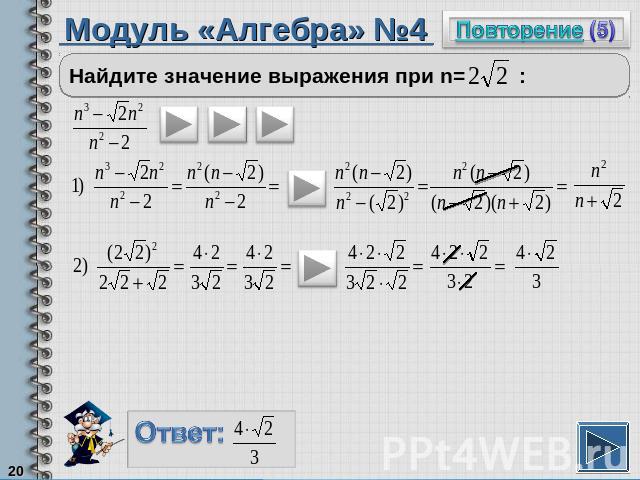
Модуль «Алгебра» №4Найдите значение выражения при n= :

Повторение (подсказка)Чтобы проще выполнить задание, надо выражение с переменными упроститьЧтобы упростить запись дроби, ее надо сократить, а для этого надо числитель и знаменатель разложить на множители.Чтобы вынести общий множитель за скобки, надо разделить каждое слагаемое на этот множитель.Чтобы записать натуральное число в виде квадрата, надо его заключить под знак квадратного корня.Чтобы «избавиться» от иррациональности в знаменателе, надо числитель и знаменатель умножить на иррациональный множитель.

Модуль «Алгебра» №4Найдите значение выражения при

Повторение (подсказка)Сначала надо выполнить действия с рациональными дробями.

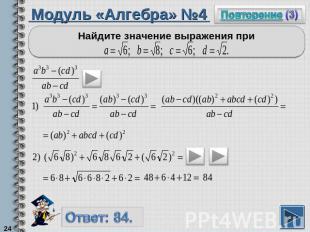
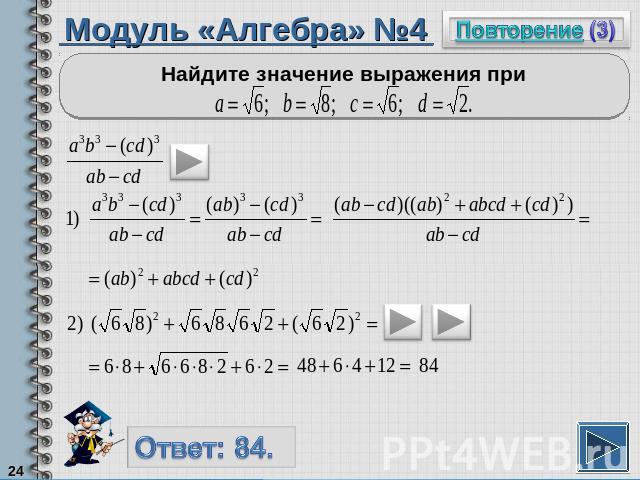
Модуль «Алгебра» №4Найдите значение выражения при

Повторение (подсказка)Числитель дроби можно записать в виде разности кубов и разложить на множители по формулеЕсли квадратный корень возвести в квадрат, то получится подкоренное число.Произведение квадратных корней из неотрицательных множителей равно квадратному корню из произведения этих множителей..

http://www.grafamania.net/uploads/posts/2008-08/1219611582_7.jpg http://www.grafamania.net/uploads/posts/2008-08/1219611582_7.jpg Автор шаблона Larisa Vladislavovna Larus http://www.proshkolu.ru/user/vladislava22/«ГИА-2013. Математика: типовые экзаменационные варианты: 30 вариантов» под редакцией А. Л. Семенова, И. В. Ященко. – М.: Изд. «Национальное образование», 2013.