Презентация на тему: геометрический метод решения систем уравнения

Геометрический метод решения систем уравнений Морозова Татьяна, МДМ-110

Метод - способ достижения какой-либо цели, решения конкретной задачи; совокупность приемов или операций практического или теоретического освоения (познания) действительности. Геометрический метод характеризуется как «метод, идущий от наглядных представлений» (А. Д. Александров), «метод геометрической наглядности» (Г. Фройденталь). Существенными признаками этого понятия являются геометрические (наглядные) представления и законы геометрии, в которых отражены свойства геометрических фигур. Геометрический метод будем понимать как способ познавательной деятельности, основанный на системе геометрических знаний и на геометрических (наглядных) представлениях.

Геометрические методы: метод длин (свойства длины отрезка); метод треугольников (система знаний о треугольниках); метод параллельных прямых (о параллельных прямых); метод соотношения между сторонами и углами треугольника (о соотношениях между сторонами и углами треугольника); метод четырехугольников (о четырехугольниках); метод площадей (о площади многоугольника); метод подобия треугольников (о подобных треугольниках); тригонометрический метод (о решении треугольников); метод окружностей (об окружности и ее элементах); метод геометрических преобразований ( о геометрических преобразованиях на плоскости и в пространстве); графический метод (о геометрическом представлении элементарных функций).

Метод уравнений состоит из следующих приемов: прием, основанный на составлении и решении линейного уравнения («прием линейного уравнения») ; прием квадратного уравнения; прием рационального уравнения; прием системы двух линейных уравнений с двумя переменными и др.

Геометрическое решение негеометрических задач (систем уравнений) Теорема Пифагора Векторный способ Формула расстояния между точками

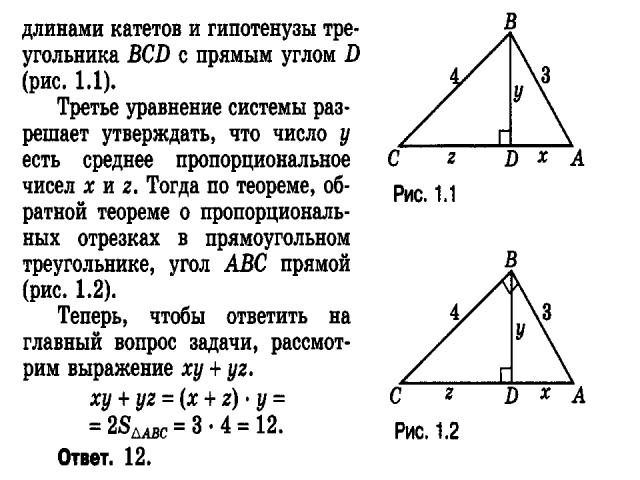
Теорема Пифагора

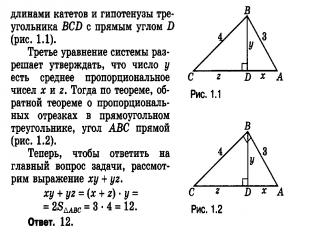
2.

Векторный способ 1.

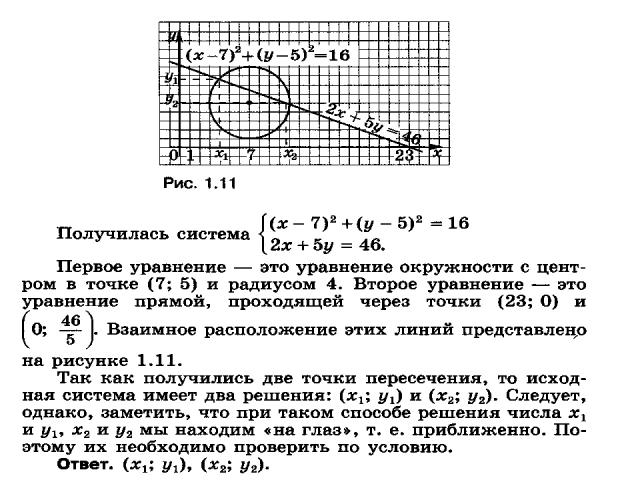
Формула расстояния между точками 1.

2.

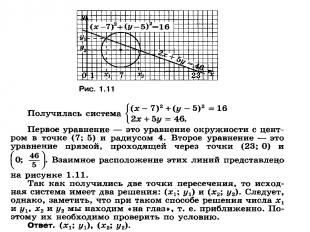
Спасибо за внимание