Презентация на тему: Четырехугольники

Курсы повышения квалификации для учителей математики Научный куратор курсов Батан Л.Ф. Проект по теме № 17 «Четырехугольники». Выполнила учитель математики МКОУ Мохнатологовская СОШ Ярославцева Алеся Александровна

Цель нашего проекта Систематизация знаний по теме «Четырехугольники»

Задачи нашего проекта: Обучающие: 1. Привести в систему теоретические знания по теме «Четырехугольники». 2. Закрепление навыков решения задач по данной теме. 4. Закрепление навыков по построению четырехугольников с использованием ИКТ. 3. Определить сферы практического использования знаний. Развивающие: 1. Развивать мысленные операции ( проведение аналогии, анализ, синтез); 2. Развивать пространственное мышление; 3. Развивать логическое мышление. Воспитывающие: 1. Развивать чувство коллективизма, умение выслушивать ответы товарищей. 2. Прививать интерес к предмету.

Прогнозируемый результ: Закрепленные теоретические знания по теме «Четырехугольники». Наличие навыков решения задач по теме. Наличие навыков по построению четырехугольников с применением ИКТ. Закрепление пути к развитию логического и пространственного мышления. Развитое чувство коллективизма.

Оборудование: Компьютеры (класс-комплект) (программа – setup «чертежник»); Видеопроектор; Раздаточный материал: - карточки с задачами; - листы с готовыми чертежами; - карточки с кроссвордами; - тесты; - черновики.

Физкультминутка:

Ход урока Организационный момент. Здравствуйте ребята! Французский писатель Анатоль Франс однажды заметил: «Учиться можно только весело… Чтобы переваривать знания, надо поглощать их с аппетитом». Давайте последуем совету писателя и проведем урок с удовольствием. Тема нашего урока: «Четырехугольники». Цель нашего урока: Систематизация знаний по теме «Четырехугольники».

Повторение основных положений теории по теме «Четырехугольники; Тестирование по теории темы «Четырехугольники». Решение задач. Работа в программе: setup «чертежник» Итоги урока.

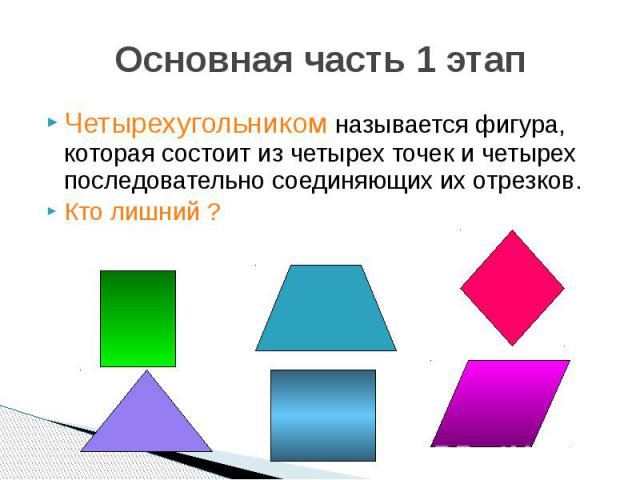
Основная часть 1 этап Четырехугольником называется фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков. Кто лишний ?

Определение параметров четырехугольника Никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться. Данные точки называются вершинами четырехугольника. А соединяющие их отрезки -сторонами четырехугольника

Свойства четырехугольника Если вершины четырехугольника являются концами одной из его сторон то их называют соседними. Вершины, не являющиеся соседними называются противолежащими. Отрезки ,соединяющие противолежащие вершины четырехугольника, называются диагоналями. Стороны четырехугольника, исходящие из одной вершины ,называются соседними Стороны не имеющие общего конца называются противолежащими

Четырехугольники

Параллелограмм Параллелограммом называется четырехугольник, у которого противолежащие стороны попарно параллельны. Свойства параллелограмма : противолежащие стороны равны; противоположные углы равны; диагонали точкой пересечения делятся пополам; сумма углов, прилежащих к одной стороне, равна 180°; сумма квадратов диагоналей равна сумме квадратов всех сторон:

Прямоугольник Прямоугольником называется параллелограмм, у которого все углы прямые. Свойства прямоугольника: все свойства параллелограмма; диагонали равны.

Квадрат: Квадратом называется прямоугольник, у которого все стороны равны. Свойства квадрата : все углы квадрата прямые; диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам. Признаки квадрата: Прямоугольник является квадратом, если он обладает каким-нибудь признаком ромба.

Ромб Ромбом называется параллелограмм, у которого все стороны равны. Свойства ромба: все свойства параллелограмма; диагонали перпендикулярны; диагонали являются биссектрисами его углов. Признаки ромба: Параллелограмм является ромбом, если: Две его смежные стороны равны. Его диагонали перпендикулярны. Одна из диагоналей является биссектрисой его угла.

Трапеция Трапецией называется четырехугольник, у которого две противолежащие стороны параллельны, а две другие не параллельны. Параллельные стороны трапеции называются ее основаниями, а непараллельные стороны — боковыми сторонами. Отрезок, соединяющий середины боковых сторон, называется средней линией. Трапеция называется равнобедренной (или равнобокой), если ее боковые стороны равны. Трапеция, один из углов которой прямой, называется прямоугольной. Свойства трапеции: ее средняя линия параллельна основаниям и равна их полусумме; если трапеция равнобокая, то ее диагонали равны и углы при основании равны; если трапеция равнобокая, то около нее можно описать окружность; если сумма оснований равна сумме боковых сторон, то в нее можно вписать окружность. Признаки трапеции : Четырехугольник является трапецией, если его параллельные стороны не равны

Крассворд «Четырехугольник» Работа в парах по заполнению кроссворда «Четырехугольники» с последующей фронтальной проверкой правильности выполнения задания. Приложение № 1

Самостоятельная работа 2 этап Часть учащихся проходит тестирование в текстовой форме с целью проверки теоретических знаний по теме. (Приложение № 2) Три ученика выполняют решение задач по теме с краткой записью у доски (возможна работа в парах) (Приложение № 3) Один ученик самостоятельно выполняет решение задачи с готовым чертежом. Приложение № 4)

Построение четырехугольников в программе setup «Чертежник» Остальная часть класса работает за компьютерами получив задание (Приложение № 5). Ребята запустите программу: setup «Чертежник». Откройте новый документ. Постройте указанный четырехугольник, обозначьте его вершины и укажите размеры сторон в (см.).

Подводим итоги урока 1 Проверяются результаты тестирования. 2. Заслушиваем учащихся у доски. 3. Проверяем решение и оформление задачи на листках. 4. Смотрим, что удалось построить ребятам используя ИКТ. 5. Выставляются оценки.

Обсуждение итогов урока: Ребята урок окончен! Давайте подумаем – все ли задачи мы выполнили которые ставили в начале урока? - обсуждение и выводы. Понравилось ли вам использовать ИКТ на уроках математики? - обсуждение и выводы. Я думаю, что урок удался. Мы будем работать дальше и будем совершенствовать свои знания совместно с использованием ИКТ. Запишите домашнее задание:

Домашнее задание: