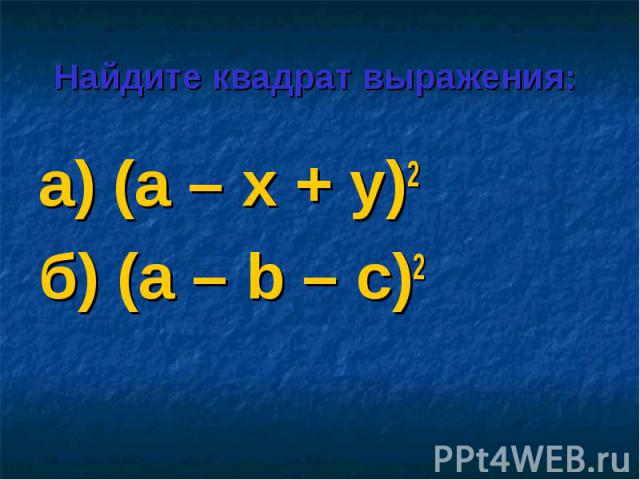Презентация на тему: Формулы сокращенного умножения 6





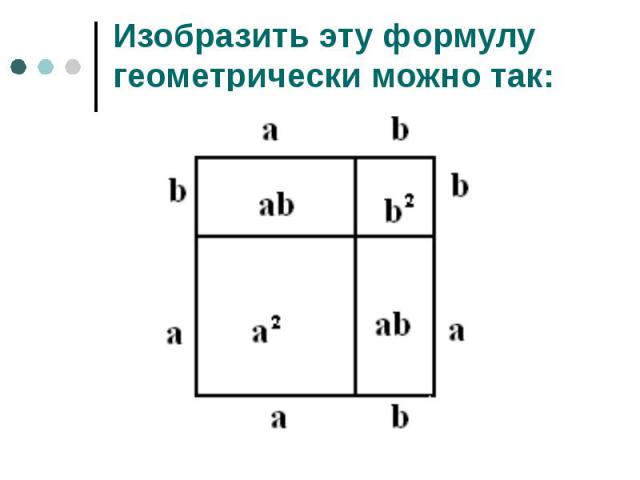
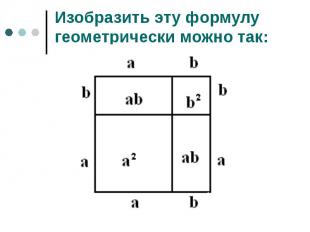
«Если отрезок как-либо разбит на два отрезка, то площадь квадрата, построенного на всем отрезке, равна сумме площадей квадратов, построенных на каждом из двух отрезков, и удвоенный площади прямоугольника, сторонами которого служат эти два отрезка.» «Если отрезок как-либо разбит на два отрезка, то площадь квадрата, построенного на всем отрезке, равна сумме площадей квадратов, построенных на каждом из двух отрезков, и удвоенный площади прямоугольника, сторонами которого служат эти два отрезка.» Суть этой фразы в формуле (а + b)2 = a2 + 2ab + b2

Словесный – понятный, но длинный, неудобный; Словесный – понятный, но длинный, неудобный; Геометрический – наглядный, но не всегда удобный для вычисления; Символьный – краткий, легко запоминающийся.



Сумма квадратов чисел а и b. Сумма квадратов чисел а и b. Разность между числом m и удвоенной суммой чисел а и b. Квадрат разности чисел b и а. Разность квадратов чисел а и b, умноженная на сумму этих чисел.


(24)х = 212; (24)х = 212; 10х = 10000; 53 54 = 52 + х; 0,1х = 0,01.

(а +…)2 = … + 2аb + … ; (а +…)2 = … + 2аb + … ; (а … b)… = а2 – 2аb + … ; а3 - … = (а – b)(… + аb + …); а3 + b3 = (… …)(а2 … + b2); а2 – b2 = (… b)(а – …).

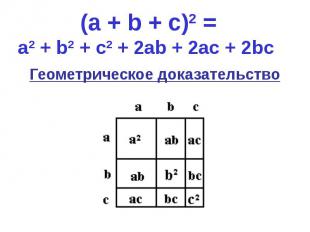
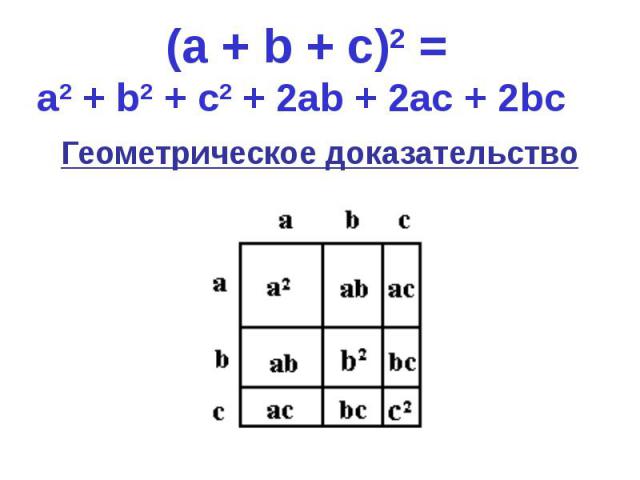
Геометрическое доказательство Геометрическое доказательство
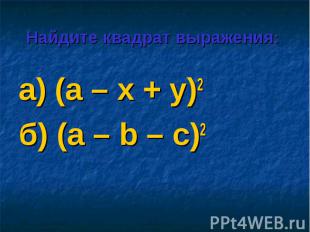
а) (а – х + у)2 а) (а – х + у)2 б) (а – b – с)2



(а + b)0 = 1 (а + b)0 = 1 (a + b)1 = a + b (a + b)2 = a2 + 2ab + b2 (a + b)3 = a3 + 3a2b + 3ab2 + b3

1 1 1 1 1 2 1 1 3 3 1

1 - 20 1 - 20 1 1 - 21 1 2 1 - 22 1 3 3 1 - 23




a2 + b2 = (a + b)2 – 2ab a2 + b2 = (a + b)2 – 2ab a2 + b2 = (a – b)2 + 2ab а2 = (a – b)(a + b) + b2


Пример. Пример. Вычислите 9862 1. Круглое число 1000. а = 986, b = 14, а + b = 1000, a – b = 972. 2. 9862 = 972 1000 + 142 = 972000 + 196 = 972196.

1) 1952 1) 1952 2) 4882



1. Обратите внимание на пирамиды чисел: 1. Обратите внимание на пирамиды чисел: а) 1 8 + 1 = 9, 12 8 + 2 = 98, 123 8 + 3 = 987. А как дальше? б) 12 = 1, 112 = 121, 1112 = ? 2. Возведите в степень: а) (2а – b + c)2; б) (а + b)4. 3. Вычислите: а) 9762; б) 2952.