Презентация на тему: Арифметическая прогрессия. Метод математической индукции

ТЕМА УРОКА: « Арифметическая прогрессия. Метод математической индукции.»

Девиз урока: « Способность к восприятию математики развита у человека пожалуй также как способность получать удовольствие от приятной музыки, она присуща огромному большинству» / Годфри Харди/

Вопросы для повторения: 1. Определение арифметической прогрессии. 2.Как найти разность арифметической прогрессии, если известны два ее члена a m и аn ,где m>n? 3. Сформулировать характеристическое свойство арифметической прогрессии ( формула). 4. Запишите формулу n-ого члена арифметической прогрессии . 5. Запишите формулу суммы n первых членов арифметической прогрессии (2 способа).

Устные упражнения: 1.Найдите член арифметической прогрессии, обозначенный буквой: 3;6; а3;12….. А)8; Б)9; В)10; Г)5. /ответ поясните/ 2.Найдите члены арифметической прогрессии, обозначенные буквами: а1;-8;а3;-4….. А)10 и 6; Б)-10 и 6; В)-10 и -6 /ответ поясните/ 3.Является ли арифметической прогрессией числовая последовательность: А)аn=n2 +5; Б)an =5n+4; В) an =(-0,5+4n):2n? /ответ поясните/ 4.Какое из чисел не является членом арифметической прогрессии:5;10;15…. А)80; Б)95; В)100; Г)112? /ответ поясните/

БУДЬ ВНИМАТЕЛЕН: Фигура состоит из столбцов как показано на рисунке. В каждом следующем столбце квадратов на два больше, чем в предыдущем. Сколько квадратов в 20-м столбце?

БУДЬ ВНИМАТЕЛЕН: Фигура составлена из квадратов, как показано на рисунке. В каждом следующем ряду квадратов на два больше, чем в предыдущем. Сколько квадратов в 15-м ряду?

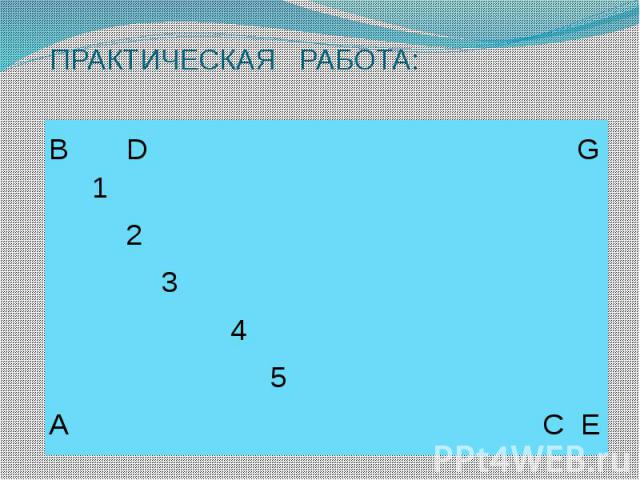
ПРАКТИЧЕСКАЯ РАБОТА:

МЕТОД МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ ЗАКЛЮЧАЕТСЯ В СЛЕДУЮЩЕМ: Утверждение, зависящее от натурального числа n , верно при любом n , если выполняются два условия: Утверждение справедливо при n =1; /базис индукции/ Из справедливости утверждения при n= k следует его справедливость при n = k +1 / индукционный шаг/.

Конструктивно- вариативный тест 1.Метод, позволяющий доказывать утверждения зависящие от натурального числа n называется методом…………………… 2.Первый шаг в доказательстве называется…………………………………………………… 3.Если утверждение справедливо при n=…….. 4.Второй шаг в доказательстве называется……………………………………………….. 5. Из справедливости утверждения при n=k следует его справедливость при n=…………..

Прогрессия в музыке. Нотная грамота: Ноты создают некоторую числовую последовательность, а именно: геометрическую прогрессию ( с ней вы познакомитесь на последующих уроках)