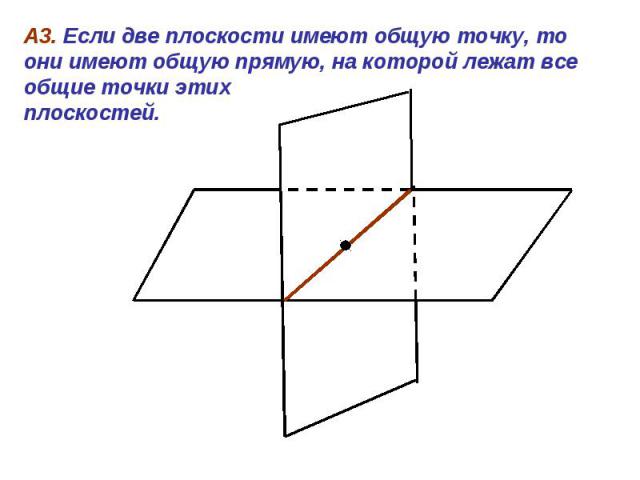
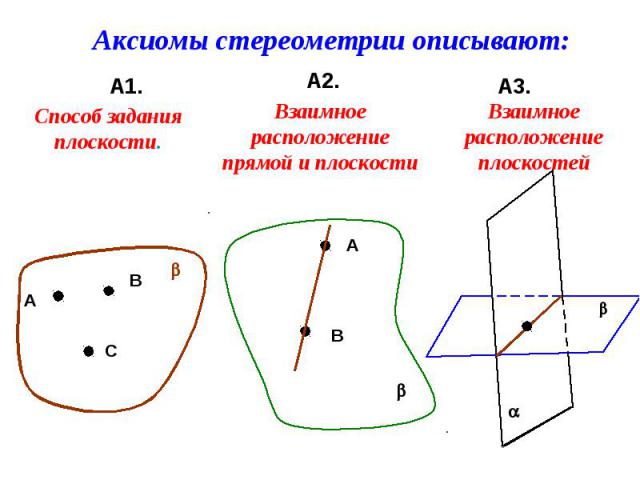
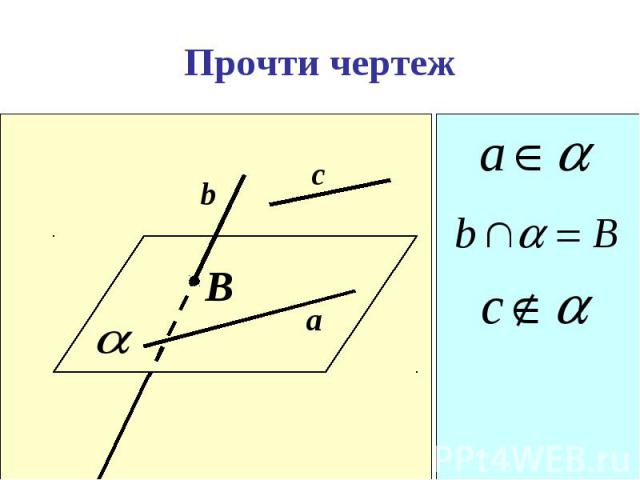
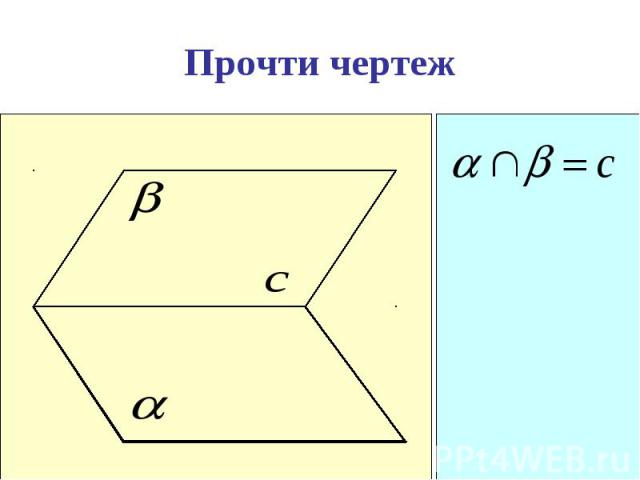
Презентация на тему: Аксиомы стереометрии

Планиметрия Планиметрия

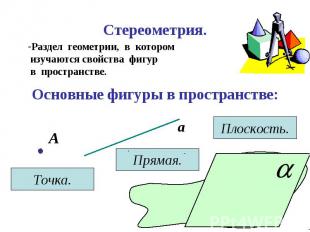
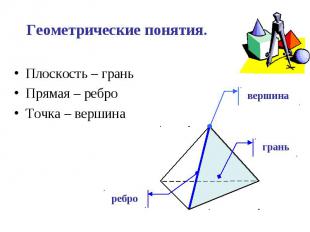
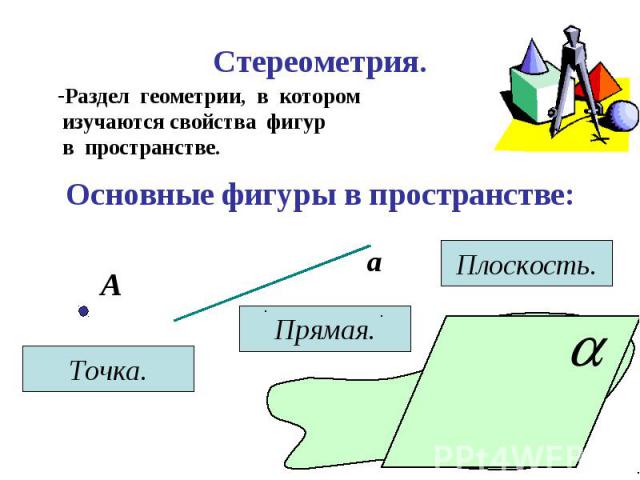
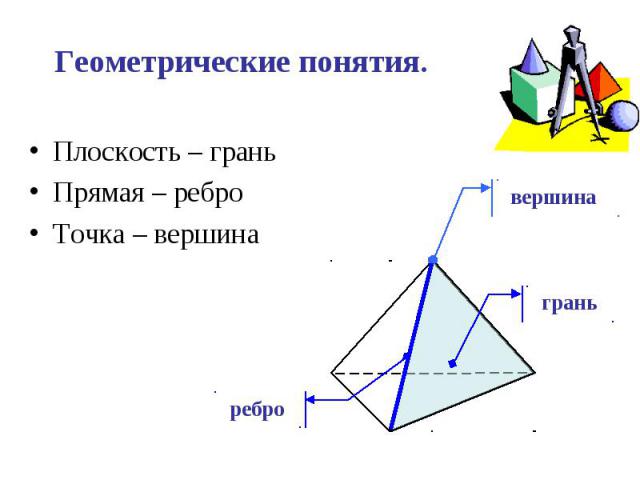
Плоскость – грань Плоскость – грань Прямая – ребро Точка – вершина

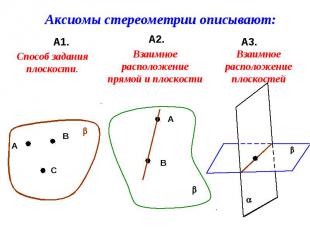
(от греч. axíõma – принятие положения) (от греч. axíõma – принятие положения)

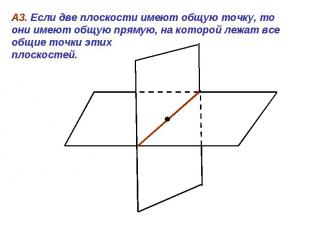
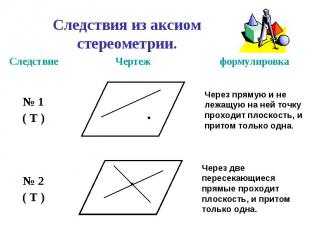
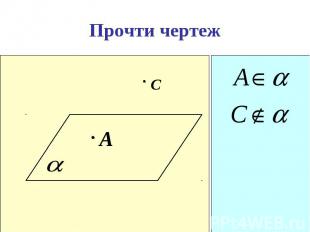
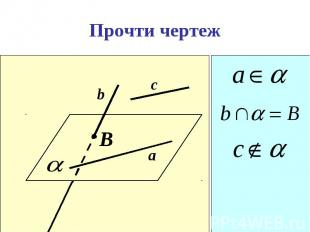
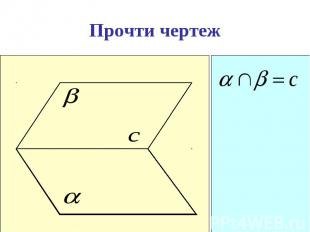
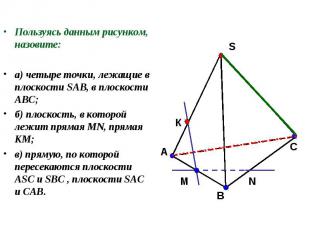
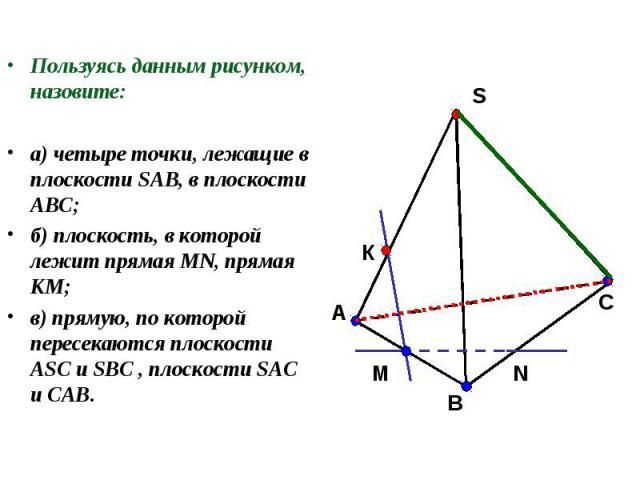
Пользуясь данным рисунком, назовите: Пользуясь данным рисунком, назовите: а) четыре точки, лежащие в плоскости SAB, в плоскости АВС; б) плоскость, в которой лежит прямая MN, прямая КМ; в) прямую, по которой пересекаются плоскости ASC и SBC , плоскости SAC и CAB.

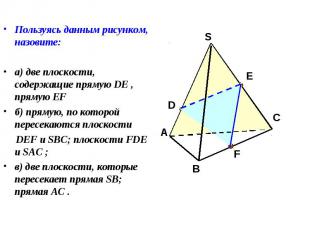
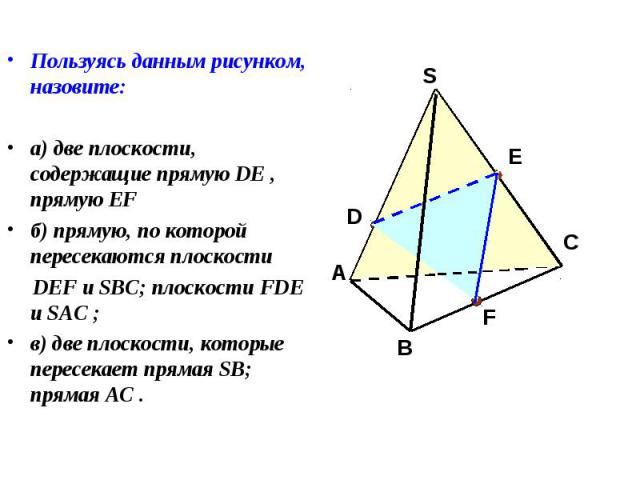
Пользуясь данным рисунком, назовите: Пользуясь данным рисунком, назовите: а) две плоскости, содержащие прямую DE , прямую EF б) прямую, по которой пересекаются плоскости DEF и SBC; плоскости FDE и SAC ; в) две плоскости, которые пересекает прямая SB; прямая AC .

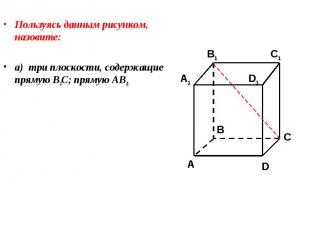
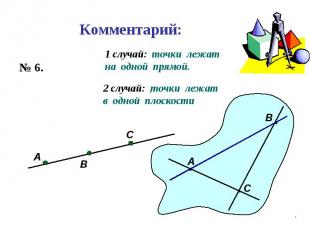
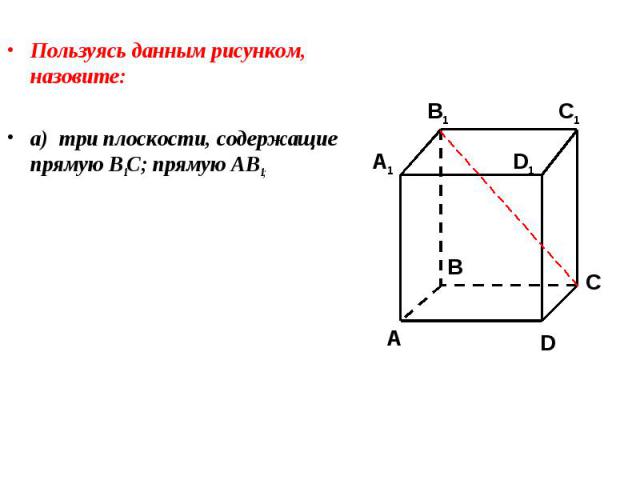
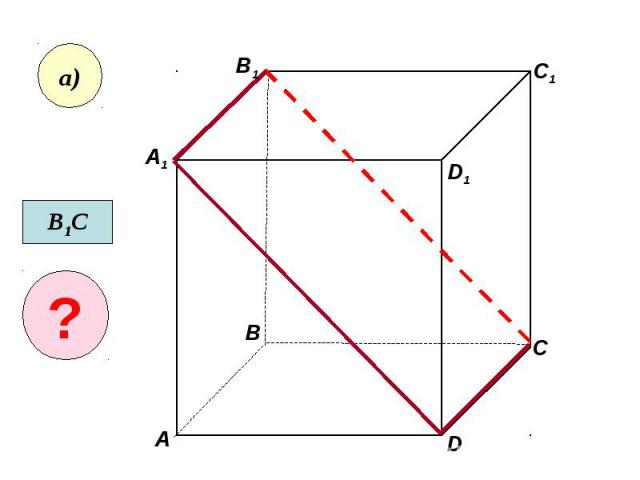
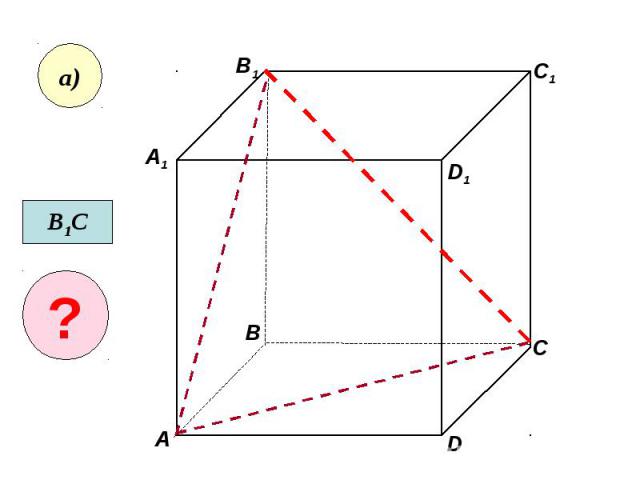
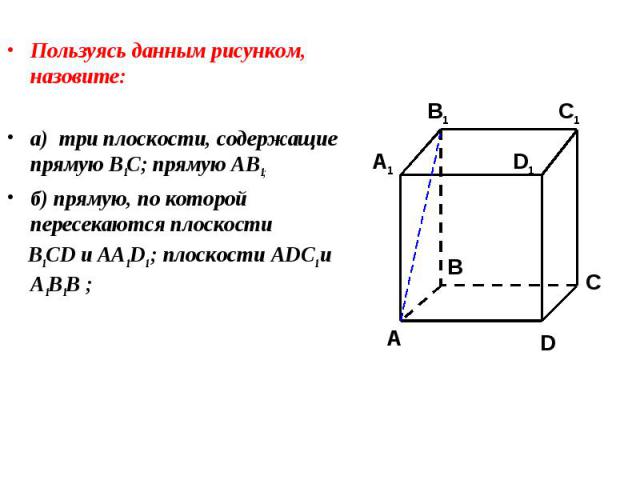
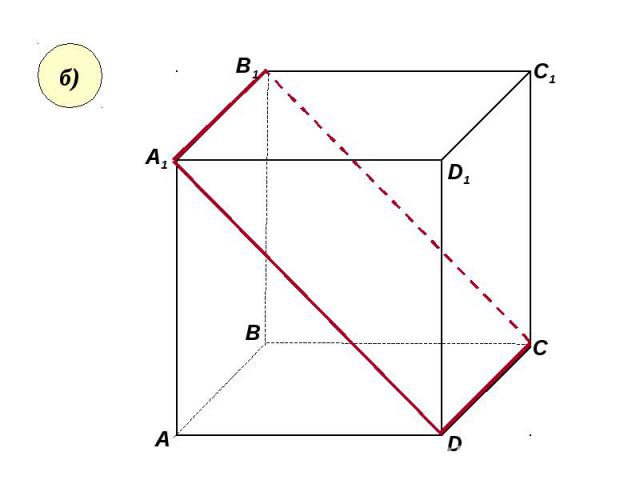
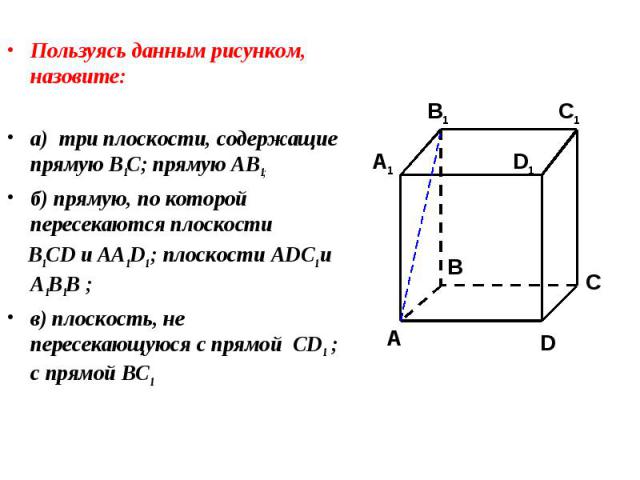
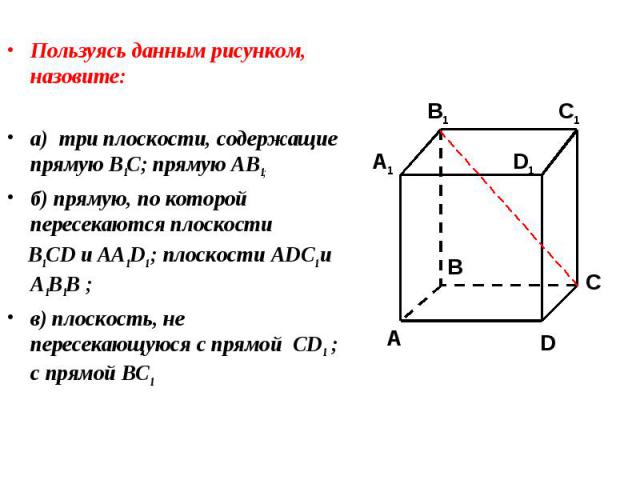
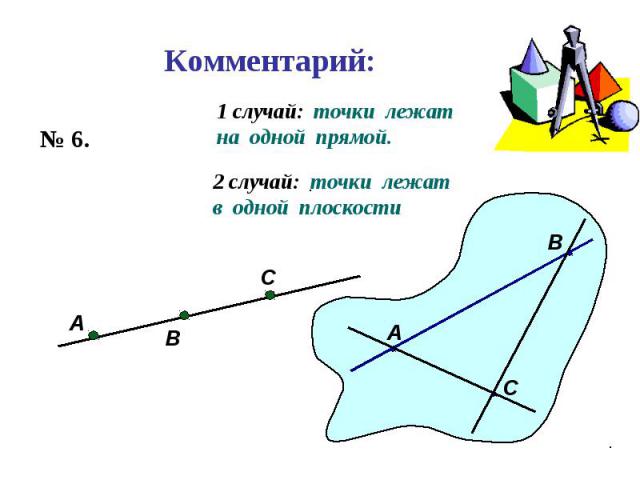
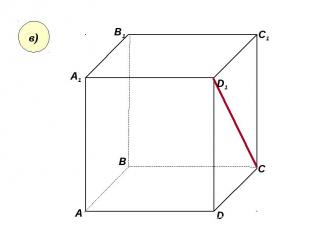
Пользуясь данным рисунком, назовите: Пользуясь данным рисунком, назовите: а) три плоскости, содержащие прямую В1С; прямую АВ1;

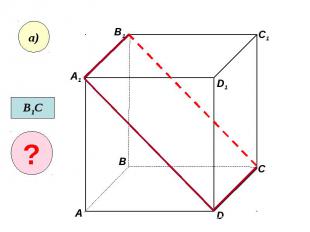
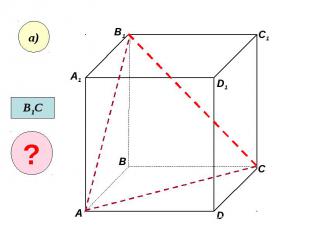
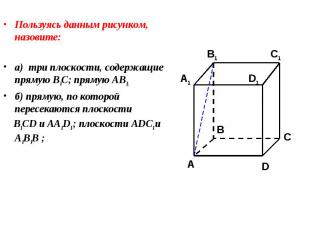
Пользуясь данным рисунком, назовите: Пользуясь данным рисунком, назовите: а) три плоскости, содержащие прямую В1С; прямую АВ1; б) прямую, по которой пересекаются плоскости B1CD и AA1D1 ; плоскости ADC1 и A1B1B ;

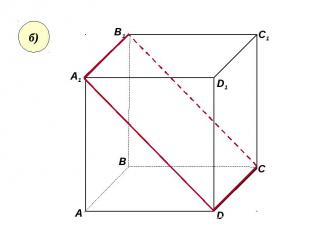
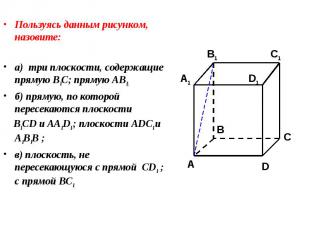
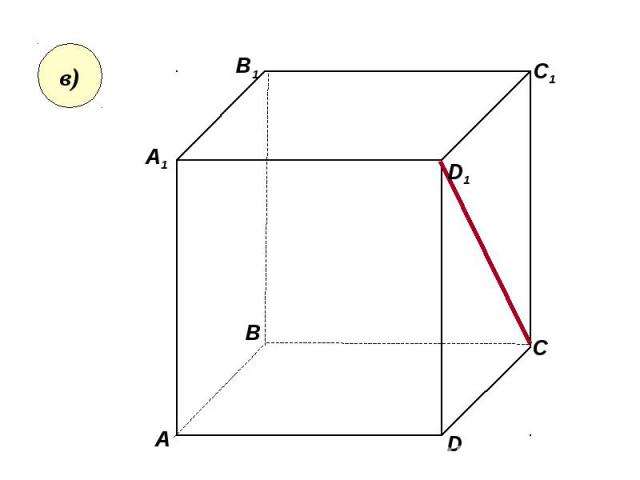
Пользуясь данным рисунком, назовите: Пользуясь данным рисунком, назовите: а) три плоскости, содержащие прямую В1С; прямую АВ1; б) прямую, по которой пересекаются плоскости B1CD и AA1D1 ; плоскости ADC1 и A1B1B ; в) плоскость, не пересекающуюся с прямой CD1 ; с прямой BC1

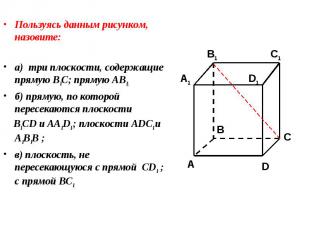
Пользуясь данным рисунком, назовите: Пользуясь данным рисунком, назовите: а) три плоскости, содержащие прямую В1С; прямую АВ1; б) прямую, по которой пересекаются плоскости B1CD и AA1D1 ; плоскости ADC1 и A1B1B ; в) плоскость, не пересекающуюся с прямой CD1 ; с прямой BC1