Презентация на тему: Использование комбинаторных задач для подсчета вероятностей

Использование комбинаторных задач для подсчета вероятностей

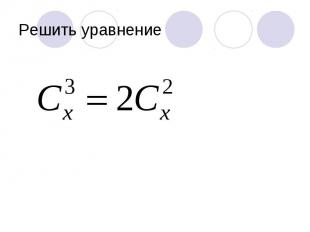
Решить уравнение

ПРИМЕР 1 Из колоды в 36 карт случайным образом вытаскивают три карты. Какова вероятность того, что среди них: нет пиковой дамы?

ПРИМЕР 1нет пиковой дамы? У нас имеется множество из 36 элементов – игральных карт. Мы производим выбор трех элементов, порядок выбора не важен. Значит имеется исходов.

ПРИМЕР 1нет пиковой дамы? Среди всех исходов нам надо сосчитать те, в которых нет пиковой дамы (событие А). Поэтому отложим даму пик в сторону и будем выбирать 3 карты из оставшихся 35 карт. Получаются все интересующие нас варианты:

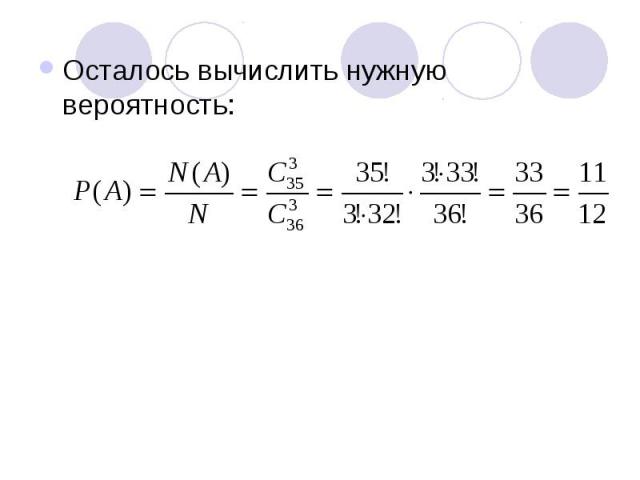
Осталось вычислить нужную вероятность:

ПРИМЕР 1Из колоды в 36 карт случайным образом вытаскивают три карты. Какова вероятность того, что среди них: есть пиковая дама?

ПРИМЕР 1 есть пиковая дама?

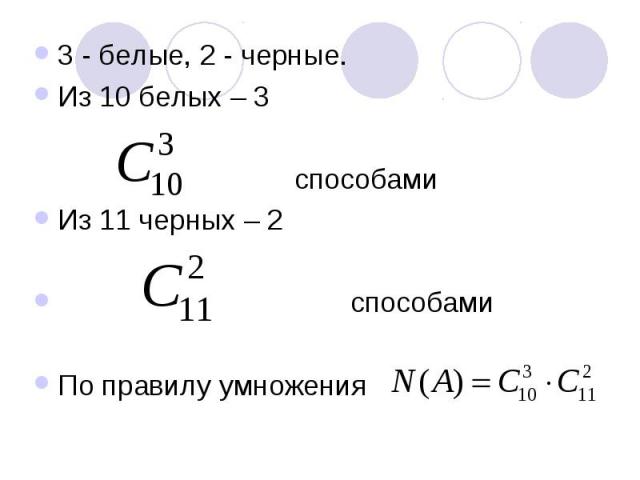
ПРИМЕР 2В урне лежит 10 белых и 11 черных шаров. Случайным образом достают 5 шаров. Какова вероятность того, что среди этих 5 шаров ровно 3 белых?

Шары в урне не различимы на ощупь. Из 21 шара случайным образом выбирают 5 шаров. Порядок не важен. Значит, существует таких выборов.

3 - белые, 2 - черные. Из 10 белых – 3 способами Из 11 черных – 2 способами По правилу умножения

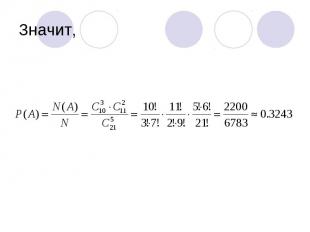
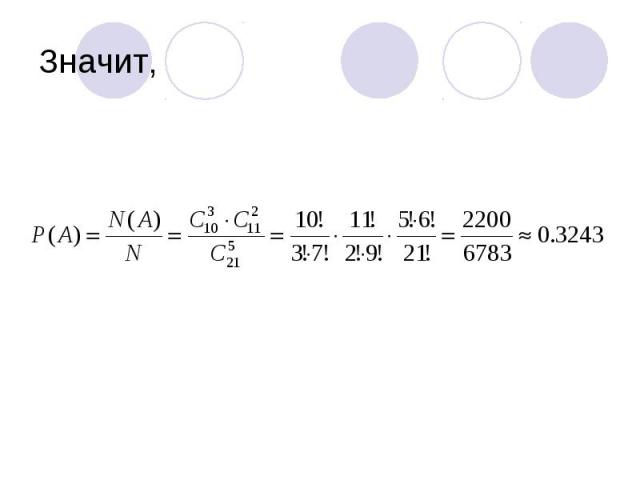
Значит,

ПРИМЕР 2В урне лежит 10 белых и 11 черных шаров. Случайным образом достают 5 шаров. Какова вероятность того, что среди этих 5 шаров не менее 4 белых шаров?

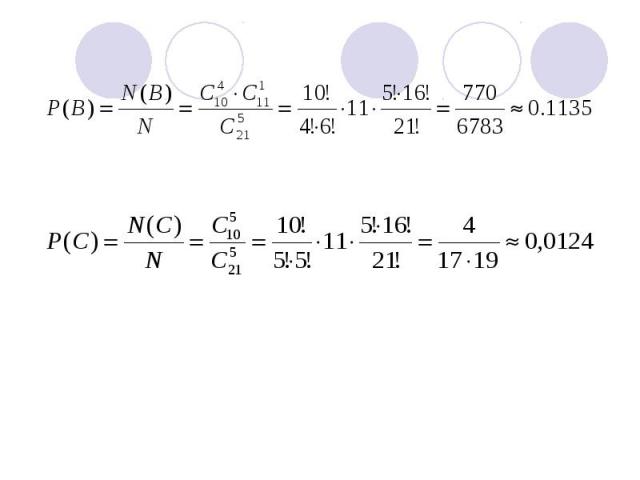
В – событие, состоящее в том, что белых шаров ровно 4, а С – событие, состоящее в том, что все 5 шаров белые.

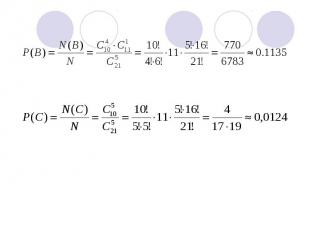
События В и С не могут наступить одновременно, т.е. они несовместимы. Вероятность суммы двух несовместимых событий равна сумме вероятностей этих событий. Значит, P(B+C)=P(B)+P(C)=0.1135+0.0124=0.1259

ПРИМЕР 2В урне лежит 10 белых и 11 черных шаров. Случайным образом достают 5 шаров. Какова вероятность того, что большинство шаров - белые?

Интересующее нас событие произойдет в следующих случаях: Из 5 шаров – 4 белых и 1 черный; 3 белых и 2 черных; Все 5 шаров белые. События не могут наступить одновременно. P(A+B+C)=P(A)+P(B)+P(C)=0.3243+ +0.1135+0.0124=0.4502

Дополнительные задачи

№1Сколько четырехбуквенных слов можно образовать из букв слова САПФИР?

Порядок важен

№1Сколько четырехбуквенных слов можно образовать из букв слова САПФИР, таких, которые не содержат буквы Р?

№1Сколько четырехбуквенных слов можно образовать из букв слова САПФИР, таких, которые начинаются с буквы С и оканчиваются буквой Р?

На 1 место – С – одним способом На последнее – Р – одним способом Остаются 4 буквы, которые размещаем по 2 местам.

№2Сколько пятибуквенных слов, каждое из которых состоит из 3 согласных и 2 гласных, можно образовать из слова УРАВНЕНИЕ? Решить с использованием треугольника Паскаля.

- выбор необходимых букв - перестановки этих 5 букв