Презентация на тему: Системы счисления

Системы счисления.

Системой счисления называется способ записи (кодирования) чисел. Все системы счисления можно разделить на две группы: позиционные и непозиционные.

Позиционной называется такая система счисления, в которой величина цифры зависит от позиции (места), занимаемой этой цифрой в записи числа.

Пример: арабская система счисления, которой мы обычно пользуемся. Если взять два числа 102 и 21, то цифра 1 в первом числе в 100 раз "тяжелее" той же цифры во втором числе. А вот цифра 2 в первом числе в 10 раз "легче" этой же цифры во втором числе.

Если же величина цифры не зависит от места, занимаемого этой цифрой, то такая система счисления называется непозиционной.

Непозиционные системы счисления первичны по своему происхождению; но поскольку они имеют ряд недостатков по сравнению с позиционными системами счисления, то постепенно они потеряли свое значение.

Алфавит Римской системы I V X L C D M 1 5 10 50 100 500 1000

Числа в римской системе счисления записываются по определенным правилам: 1) если большая цифра стоит перед меньшей, они складываются, например: VI=6;

2) если меньшая цифра стоит перед большей, то из большей вычитается меньшая, причем в этом случае меньшая цифра уже повторяться не может, например: XL=40, XXL-нельзя; 3) цифры M,C,X,I могут повторяться в записи числа не более трех раз подряд; 4) цифры D,L,V могут использоваться в записи числа только по одному разу.

Например число 1996 будет записано в римской система счисления как MCMXCVI.

Самое большое число, которое можно записать в этой системе счисления, это число 3999 MMMCMXCIX. Для записи еще больших чисел пришлось бы вводить еще новые обозначения.

А теперь попробуйте выполнить простую арифметическую операцию, не переводя числа в привычную систему счисления: умножить число CLVI на число LXXIV. Вряд ли вам это удастся.

Недостатки непозиционных систем счисления: а) нельзя записывать сколь угодно большие числа; б) запись чисел обычно громоздка и неудобна; в) математические операции над числами крайне затруднены. Именно поэтому, хотя римская и очень "красивая" система счисления, она не получила широкого распространения.

Вопросы и упражнения. 1. Что такое система счисления ? 2. В чем отличие позиционной системы счисления от непозиционной ? 3. Во сколько раз цифра 5 "тяжелее" в первом числе по сравнению с этой же цифрой второго числа: 15243 и 750 ? 4. Во сколько раз первая цифра 3, встречающаяся в числе "тяжелее" второй такой же цифры а) 33765 ; б) 37653 ?

Вопросы и упражнения. 5. Почему двоичная система счисления получила широкое распространение? 6. Почему непозиционные системы счисления потеряли свое значение ? 7. Приведите примеры, где римские цифры используются в наше время. 8. Перемножьте числа 23 и 17. Запишите все три числа в римской системе счисления.

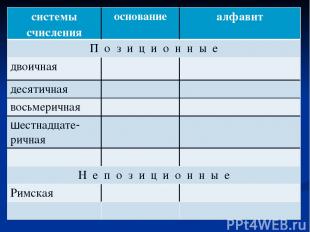
системы счисления основание алфавит П о з и ц и о н н ы е двоичная десятичная восьмеричная шестнадцате-ричная Н е п о з и ц и о н н ы е Римская

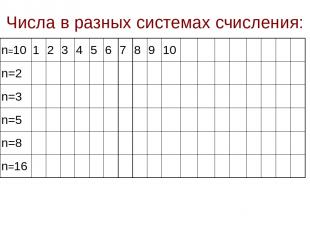
Числа в разных системах счисления: n=10 1 2 3 4 5 6 7 8 9 10 n=2 n=3 n=5 n=8 n=16

Семакин стр.36-38

Перевод из десятичной системы в двоичную Принцип: делить число на 2 и собирать остатки от деления в обратном порядке. Показать на примерах

Что больше 1 или 9? (Понятно что 9). Но в числе 13509 важнее играет роль 1. И это всем понятно так как мы привыкли с начальной школы читать это число следующим образом: начиная слева цифру умножаем на соответствующий разряд в котором она находится складываем со следующей цифрой, умноженной на свой соответствующий разряд и т.л., пока не дойдем до последней цифры.

10000 1000 100 10 1 - разряды 1 3 5 0 9 = = 1*10000 + 3*1000 + 5*100 + 9*1 = = 1*10 4+ 3*10 3 + 5*10 1 + 9*10 0

Можно рассматривать системы счисления и с другими основаниями. Если р - основание системы счисления, то любое число N в этой системе счисления может быть представлено в виде N =а(n)*р^n + a(n-1)*p^(n-1) + ... + a(1)*p + a(0), где коэффициенты - цифры р-ичной системы счисления.

Перевод чисел в десятичную СС из других СС осуществляется с помощью записи их в виде суммы степеней основания : N =а(n)*рn + a(n-1)*p(n-1) + ... + a(1)*p + a(0), где р - основание системы счисления, коэффициенты - цифры р-ичной системы счисления.

Показать принцип на примерах

пример: переведем число 542 из 8-ричной в десятичную СС. Для этого представим число 542 в виде суммы степеней основания 8: 5428 = 5*8 2 + 4*8 1 + 2*8 0 . Теперь произведем вычисления: 5*8 2 + 4*8 1 + 2*8 0 = 5*64 + 4*8 +2*1= 320 + 32 +2 = 35410. Таким образом, 5428 = 35410.

Еще примеры: 3В916 = 3*16 2 + 11*16 1 + 9*16 0 = =3*256 + 11*16 + 9*1 = 95310. 110101 = 1*2 5 + 1*2 4 + 0*2 3 + 1*2 2 +1*0 1 + 1*2 0 = =32 + 16 + 0 + 4 + 0 +1 = 5310.

Самостоятельная работа: Перевести в двоичную систему : 3610 , 25510 , 34510 , 50210 . Перевести в десятичную систему : 10000112 , 111001112 , 1000010102 .