Презентация на тему: Системы счисления

Системы счисления
Системы счисления Непозиционные Позиционные

Непозиционные системы счисления В таких системах счисления величина, которую обозначает знак в записи числа не зависит от положения этого знака в записи числа. Пример: Римская система записи чисел: I V X L C D M 1 5 10 50 100 500 1000 CCXXXII 200 + 30 + 2 = 232 VI -6 IV - 4

Позиционные системы счисления В таких системах счисления величина, которую обозначает знак в записи числа зависит от положения этого знака в записи числа. Основание системы счисления – количество цифр, используемых для записи чисел в данной системе счисления. Пример: Десятичная система счисления Основание - 10 Цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9

Пример: Двоичная система счисления Основание - 2 Цифры: 0, 1 Пример: Пятеричная система счисления Основание - 5 Цифры: 0, 1, 2, 3, 4

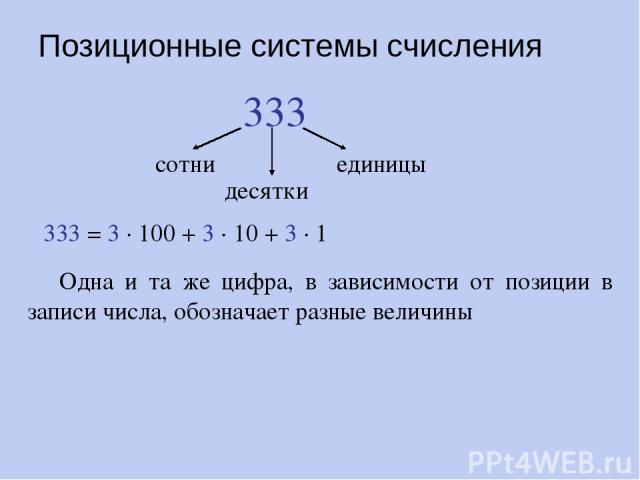
Позиционные системы счисления 333 сотни десятки единицы 333 = 3 · 100 + 3 · 10 + 3 · 1 Одна и та же цифра, в зависимости от позиции в записи числа, обозначает разные величины

Позиционные системы счисления Основанием позиционной системы счисления может быть любое натуральное число, большее 1. n >1 Если основание системы счисления n 10, то для записи чисел в данной системе счисления используются первые n арабских цифр. Если основание системы счисления n 10, то для записи чисел в данной системе счисления используются 10 арабских цифр (1, 2,…, 9) и буквы.

основание алфавит название n= 2 0, 1 Двоичная n=3 0, 1, 2 Троичная n=8 0, 1, 2, 3, 4, 5, 6, 7 Восьмеричная n=16 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B. C, D, E, F Шестнадцатеричная 101002 –число в двоичной системе счисления 5418 – число в восьмеричной системе счисления 3B8F16 - число в шестнадцатеричной системе счисления

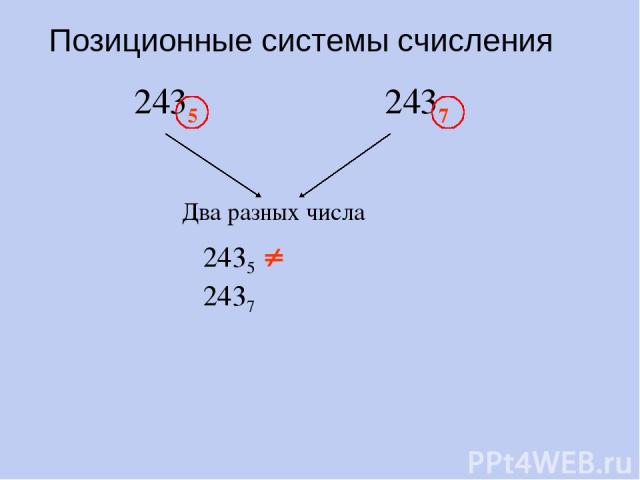
Позиционные системы счисления 2435 2437 Два разных числа 2435 2437

Позиционные системы счисления 45910 = 4 · 100 + 5 · 10 + 9 · 1 = = 4 · 102 + 5 · 101 + 9 · 100 Развёрнутая форма записи числа 345,52= 3 · 100 + 4 · 10 + 5 · 1 +5 · 0,1 + 2 · 0,01 = = 3 · 102 + 4 · 101 + 5 · 100 +5 · 10-1 + 2 · 10-2 1245 = 1 · 52 + 2 · 51 + 4 · 50 = 25 + 10 + 4 = 3910