Презентация на тему: Представление чисел в памяти компьютера

Представление чисел в памяти компьютера 10 класс. Профильный уровень

Сегодня вы познакомитесь с алгоритмом представления целых чисел в компьютере; Развивающая: способствовать развитию у  учащихся интереса к теоретическим основам фундаментальных наук – теории информатики и математических основ информационных технологий. Воспитательная: обеспечить условия для формированию у учащихся таких качеств как точность и внимательность.

* Перевести числа: 15610= ?2 11102= ?10 На выполнение задания 2 мин.

* Проверка 15610=100111002 11102=1410

Выполнить действия в двоичной системе счисления 10011100-110000= 1101100+11100= 111101 -1001011= На выполнение задания 2 мин.

Проверка 1101100 +11100 10001000 10011100 -110000 1101100

Учебная задача: научиться записывать целые отрицательные числа в машинных кодах, использовать полученные знания при сложении чисел с разными знаками. *

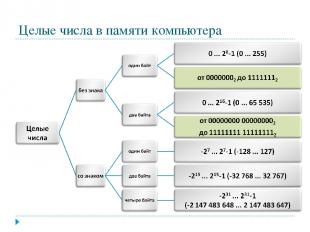
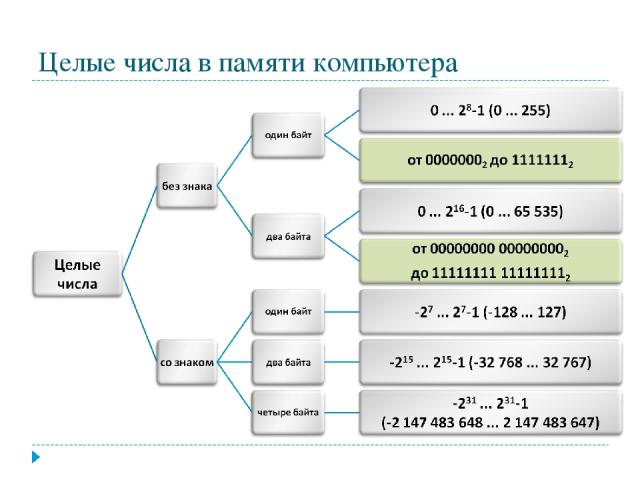
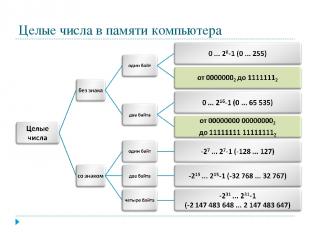
Целые числа в памяти компьютера

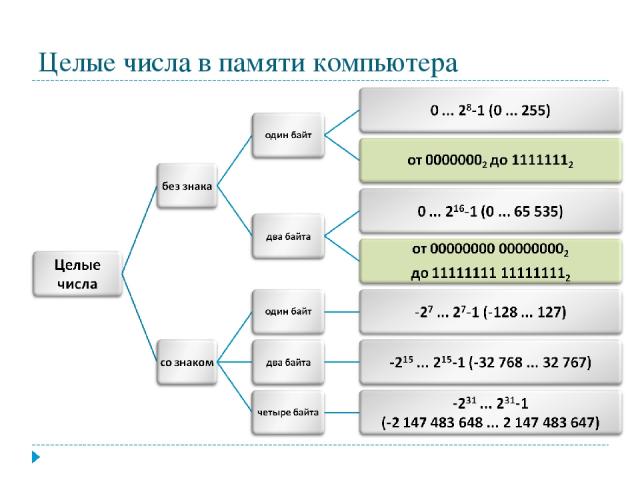
Представление чисел в формате с фиксированной запятой Для хранения целых неотрицательных чисел отводится одна ячейка памяти (8 бит). Минимальное число 00000000 Число в n-разрядном представлении 2n-1 Максимальное число 28-1=25510 или 11111111

Числа без знака Число 3910 = 100111 2 в однобайтовом формате: Число 3910 = 100111 2 в двубайтовом формате: Число 65 53510 = 11111111 111111112 в двубайтовом формате:

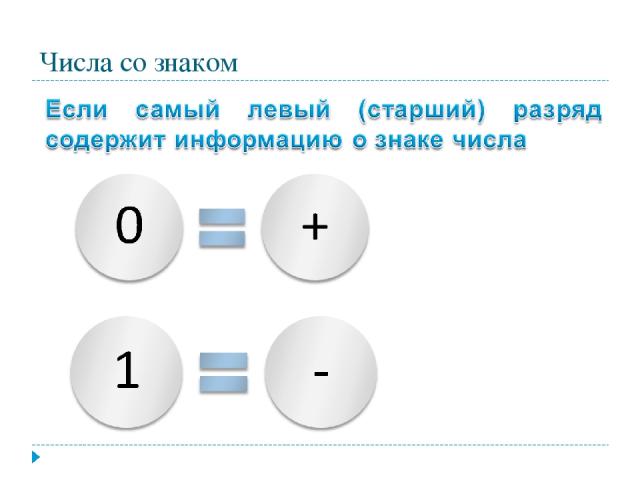
Хранение целых чисел со знаком Для хранения отводится 1 или 2 ячейки памяти (8 или 16 бит) Старший (левый) разряд отводится под знак.

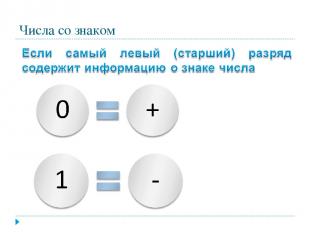
Числа со знаком

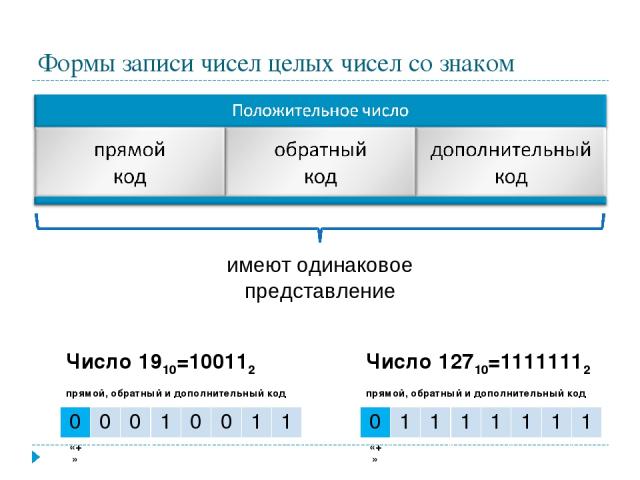
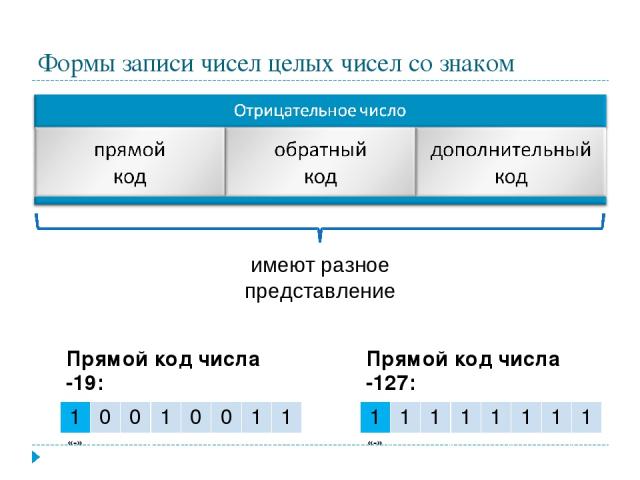
Формы записи целых чисел со знаком

Прямой код числа Это -представление в компьютере положительных чисел с использованием формата «знак – величина». Пример: 200210=111110100102 В 16-ти разрядном представлении 0 0 0 0 0 1 1 1 1 1 0 1 0 0 1 0

При представлении целых чисел в n-разрядном представлении со знаком максимальное положительное число А=2n-1 - 1

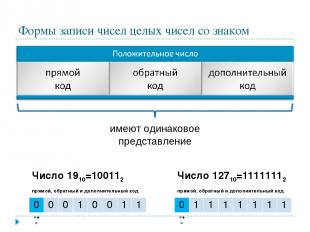
Формы записи чисел целых чисел со знаком имеют одинаковое представление Число 1910=100112 прямой, обратный и дополнительный код 0 0 0 1 0 0 1 1 «+» Число 12710=11111112 прямой, обратный и дополнительный код 0 1 1 1 1 1 1 1 «+»

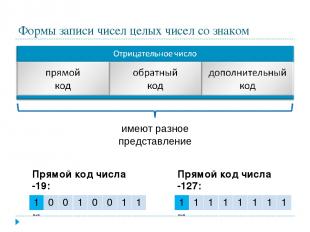
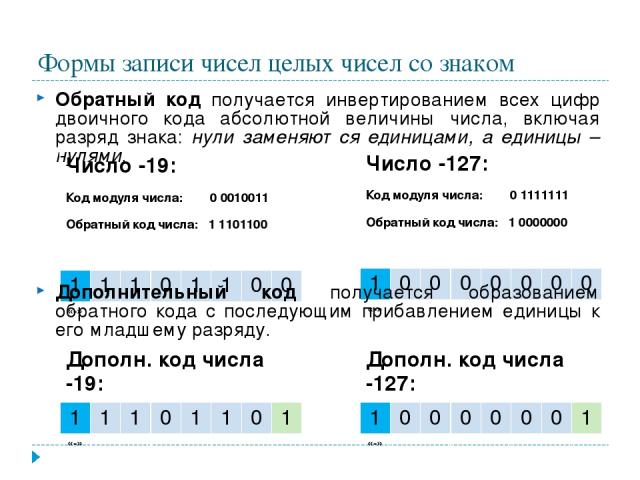
Формы записи чисел целых чисел со знаком имеют разное представление Прямой код числа -19: 1 0 0 1 0 0 1 1 «-» Прямой код числа -127: 1 1 1 1 1 1 1 1 «-»

Формы записи чисел целых чисел со знаком Обратный код получается инвертированием всех цифр двоичного кода абсолютной величины числа, включая разряд знака: нули заменяются единицами, а единицы – нулями. Дополнительный код получается образованием обратного кода с последующим прибавлением единицы к его младшему разряду. Число -19: Код модуля числа: 0 0010011 Обратный код числа: 1 1101100 1 1 1 0 1 1 0 0 «-» Число -127: Код модуля числа: 0 1111111 Обратный код числа: 1 0000000 1 0 0 0 0 0 0 0 «-» Дополн. код числа -19: 1 1 1 0 1 1 0 1 «-» Дополн. код числа -127: 1 0 0 0 0 0 0 1 «-»

Дополнительный код Используется для представления отрицательных чисел Позволяет заменить арифметическую операцию вычитания операцией сложения, что упрощает работу процессора и увеличивает его быстродействие. Дополнительный код отрицательного числа А, хранящегося в n – ячейках, равен 2n-|A|

Арифметические действия

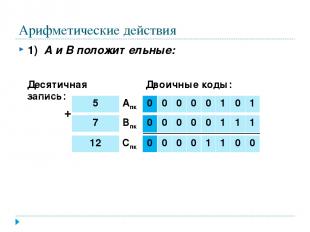
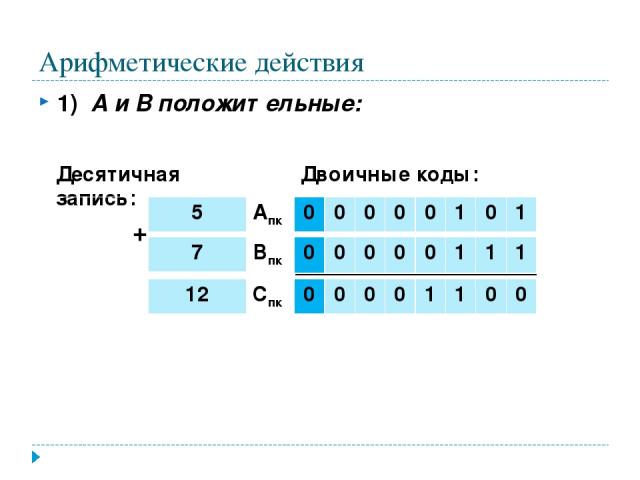
Арифметические действия 1) А и В положительные: + Десятичная запись: Двоичные коды: 12 Спк 0 0 0 0 1 1 0 0 7 Впк 0 0 0 0 0 1 1 1 5 Апк 0 0 0 0 0 1 0 1

Арифметические действия 2) А – положительное, В – отрицательное, |B|>|A| При переводе в прямой код биты цифровой части результата инвертируются и к младшему разряду прибавляется единица: 10000110 + 1 = 10000111= -710 + Десятичная запись: Двоичные коды: -7 Сдк 1 1 1 1 1 0 0 1 -12 Вдк 1 1 1 1 0 1 0 0 5 Апк 0 0 0 0 0 1 0 1

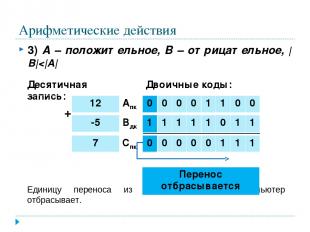
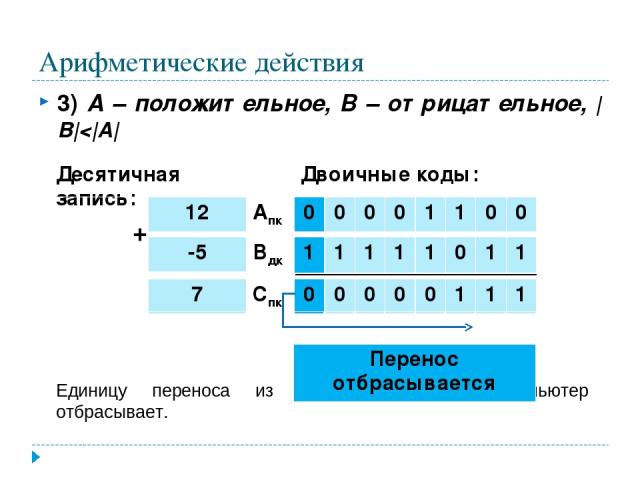
Арифметические действия 3) А – положительное, В – отрицательное, |B|

Арифметические действия 4) А и В отрицательные При переводе в прямой код биты цифровой части результата инвертируются и к младшему разряду прибавляется единица: 10001011+1= 10001100= -1210 + Десятичная запись: Двоичные коды: -12 Сдк 1 1 1 1 0 1 0 0 -7 Вдк 1 1 1 1 1 0 0 1 -5 Адк 1 1 1 1 1 0 1 1 Перенос отбрасывается

Целые числа в памяти компьютера

Вернемся к заданию №2. Решите данный пример 111101 -1001011

Проверка 111101 -1001011 При переводе в прямой код биты цифровой части результата инвертируются и к младшему разряду прибавляется единица: 10001101 + 1 = 10001110= -1410 + 61 Апк 0 0 1 1 1 1 0 1 -75 Вдк 1 0 1 1 0 1 0 1 -14 Сдк 1 1 1 1 0 0 1 0

Упражнение 1 Определить максимальное положительное число, которое может храниться в оперативной памяти в формате целое число со знаком в двухбайтном представлении.

Решение А=2n-1 – 1 А10=215 – 1 = 3276710

Упражнение 2. Получить 8-разрядный дополнительный код числа -52:

Решение. 00110100 - число |-52|=52 в прямом коде 11001011 - число  -52  в обратном коде 11001100 - число  -52  в дополнительном коде

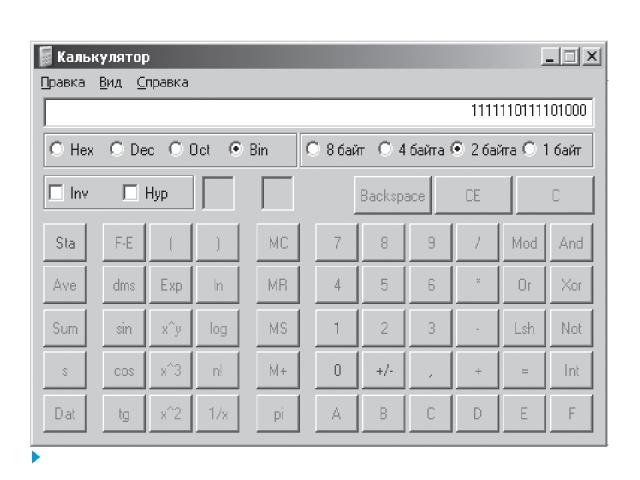
Практическая работа Задание. Получить прямой, обратный и дополнительный коды для числа -536 в формате «Знак» – «величина» в 16-разрядном представлении Провести проверку решения на калькуляторе.

Практическая работа Решение. модуль числа -536 будет равен 0000001000011000, обратный код – 1111110111100111, дополнительный код – 1111110111101000.

Практическая работа Проверка на калькуляторе. Ввести значение модуля числа -536, т. е. число 536 в строку ввода с помощью опционной кнопки Bin преобразуем это число, представленное в десятичной системе счисления, в двоичную систему, предварительно установив опционную кнопку 2 байта.  Нажав кнопку Not калькулятора, получим обратный код числа. прибавив к обратному коду двоичную единицу,  – дополнительный код. Получился окончательный результат

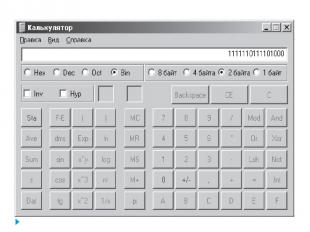
Практическая работа Проверка на калькуляторе. Можно поступить еще проще: набрав на калькуляторе число -536 и активизировав кнопку Bin, получить дополнительной код этого числа в двоичной системе счисления.