Презентация на тему: Системы счисления

Системы счисления

Основные понятия систем счисления Что называют системой счисления? Какие виды систем счисления бывают? Приведите примеры систем счисления. Системой счисления или нумерацией называется определенный способ записи чисел. Унарные, непозиционные и позиционные

Основные понятия позиционных систем счисления Что является основой любой позиционной системы счисления? Что образуют цифры в совокупности? Как будет называться количество цифр в алфавите? Цифра – символ, используемый для записи чисел. Алфавит – системы счисления – совокупность всех цифр. Размерность алфавита – количество цифр в алфавите.

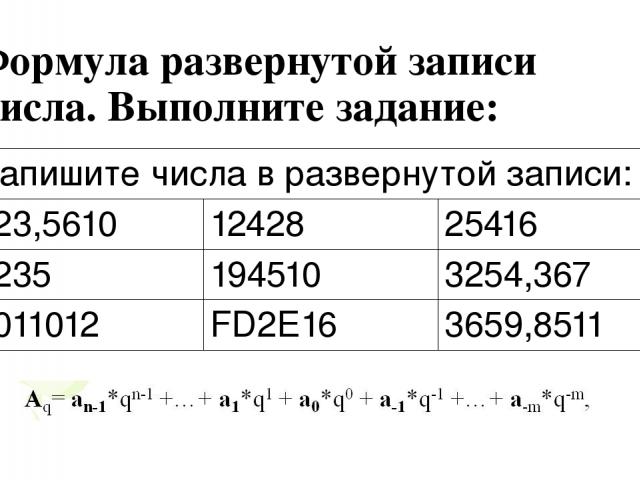
Формула развернутой записи числа. Выполните задание: Запишите числа в развернутой записи: 123,5610 12428 25416 1235 194510 3254,367 1011012 FD2E16 3659,8511

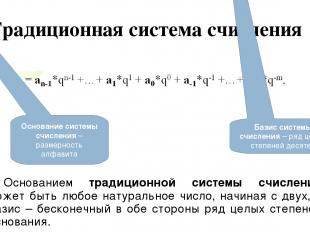
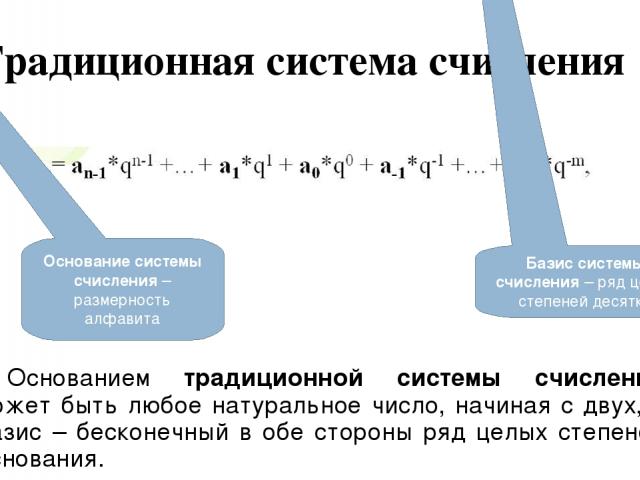
Традиционная система счисления Основанием традиционной системы счисления может быть любое натуральное число, начиная с двух, а базис – бесконечный в обе стороны ряд целых степеней основания. Основание системы счисления – размерность алфавита Базис системы счисления – ряд целых степеней десятки

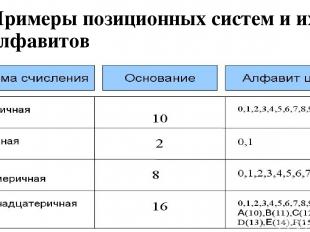
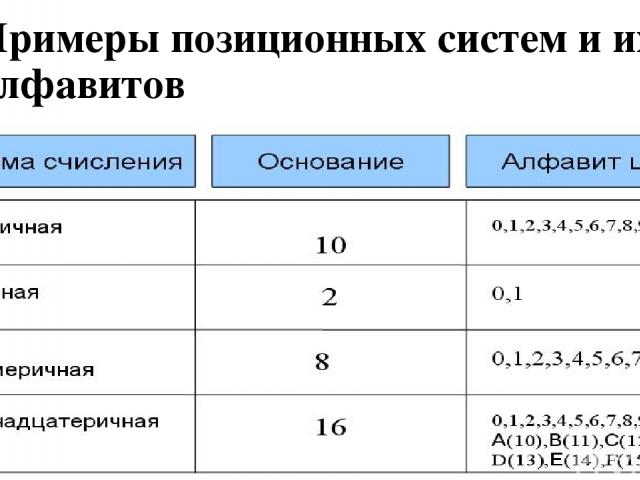
Примеры позиционных систем и их алфавитов

Выполним следующие задания: Задача №1. Число в троичной системе счисления: 2011,13 нужно перевести в десятичную систему. Задача №2. Шестнадцатеричное число 2AF,8C16 перевести в десятичную систему. Задача №3. Двоичное число 1010101111,1000112 перевести в десятичную систему.

Схема Горнера и перевод чисел целых чисел   Старшую цифру умножаем на основание, добавляем вторую цифру, результат умножаем на основание, добавляем третью цифру и так до тех пор, пока не прибавим последнюю цифру.   Результатом будет десятичная запись числа. Ясно, что полученное равенство будет справедливо для любых целых P-ичных чисел, а формулу можно записать в общем виде: anan-1an-2...a1a0p=(...(an*p+an-1)*p+an-2)*p+...)+a1)*p+a0.  Эта формула и является иллюстрацией схемы Горнера для перевода целых чисел в десятичную систему счисления.   Показать как переводить дробные числа.

Нетрадиционная система счисления (числа Фибоначчи). Алфавит фибоначчиевой системы счисления из двух цифр 0 и 1. Базисом этой системы является следующий ряд чисел: 1, 2, 3, 5, 8, 13, 21, 34, …. Он называется рядом Фибоначчи или числами Фибоначчи. Ряд Фибоначчи строиться следующим образом. Первые два число F1=1 и F2=2. Каждое следующее равно сумме двух предыдущих чисел.

Особенность Фибоначчиевой системы.

Перевод десятичных чисел в другие системы счисления. Перевод целого числа Перевод дробного числа Рассказать суть способа перевода используя схему Горнера. И связать с Паскалем (mod и div), для первого и второго случая.

Перевод целого числа (пример) Задача №4. Перевести число 5810 в троичную систему счисления. Задача №5. Перевести число 12110 в пятеричную систему счисления.

Перевод дробного числа Первая ситуация: после некоторого числа умножений в дробной части произведения получился 0. Задача №6. Перевести десятичную дробь 0,625 в двоичную систему счисления.

Перевод дробного числа Вторая ситуация: Получение периодической дробной части. В таком случае последовательные умножения надо продолжать до выделения дробной части. Задача №7. Перевести число 0,24610 в пятеричную систему счисления.