Презентация на тему: Системы счисления

Системы счисления Выполнилстудент группы04-РРТШамринКонстантин

Содержание 1. Представление о системах счисления. Однородные позиционные системы счисления. Многочленное представление числа. Веса разрядов 2. Преобразование целых чисел из одной системы счисления в другую 3. Перевод правильных дробей и одной системы счисления в другую 4. Сложение-вычитание целых беззнаковых чисел 5. Представление знакопеременных чисел и сложение-вычитание чисел со знаком 6. Двоичное умножение 7. Двоичное деление целых чисел 8. Коды Хемминга

Представление о система счисления. Однородные позиционные системы счисления. Многочленное представление числа. Веса разрядов. Система счисления (далее СС) - совокупность приемов и правил для записи чисел цифровыми знаками. Наиболее известна десятичная СС, в которой для записи чисел используются цифры 0,1,:,9. Способов записи чисел цифровыми знаками существует бесчисленное множество. Любая предназначенная для практического применения СС должна обеспечивать:возможность представления любого числа в рассматриваемом диапазоне величин; единственность представления (каждой комбинации символов должна соответствовать одна и только одна величина); простоту оперирования числами; Все системы представления чисел делятся на позиционные и непозиционные. Запись чисел может быть представлена в виде, k А (Д) = Д1 + Д2 + …+ ДK = Дi i=1 где A (D) - запись числа A в СС D; Di - символ системы, образующие базу. Поэтому принципу построены непозиционные СС. Непозиционная СС - система, для которой значение символа не зависит от его положения в числе.

В общем же случае системы счисления: A (B) =a1B1+a2B2+...+anBn. Если положить, что Bi=qi*Bi-1, а B1=1, то получим позиционную СС. Если при этом qi=q, то, очевидно, Bi=qi, и система называется однородной позиционной. При этом натуральное число q называют базисом системы, а цифры ai принимают целые значения от 0 до q-1. Число A записывается так: anan-1...a1. После последовательности цифр иногда указывают основание той СС, в которой число записано, например число 9 в двоичной форме записывается так: 1001 (2). При q=10 мы имеем дело с привычной нам десятичной СС. На практике также используют другие СС: Каждая СС имеет свои правила арифметики (таблица умножения, сложения). Поэтому, производя какие-либо операции над числами, надо помнить о СС, в которой они представлены.
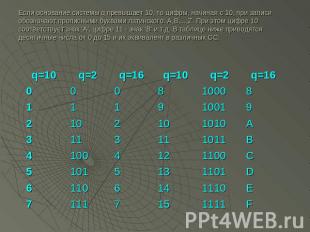
Если основание системы q превышает 10, то цифры, начиная с 10, при записи обозначают прописными буквами латинского: A,B,...,Z. При этом цифре 10 соответствует знак 'A', цифре 11 - знак 'B' и т.д. В таблице ниже приводятся десятичные числа от 0 до 15 и их эквивалент в различных СС:

В однородной позиционной СС число можно представить через его цифры с помощью следующего многочлена относительно q:A=a1*q0+a2*q1+...+an*qn (1) Выражение (1) формулирует правило для вычисления числа по его цифрам в q-ичной СС. Для уменьшения количества вычислений пользуются т.н. схемой Горнера. Она получается поочередным выносом q за скобки: A=(...((an*q+an-1)*q+an-2)*q+...)*q+a1 результат вычисления многочлена будет всегда получен в той системе счисления, в которой будут представлены цифры и основание и по правилам которой будут выполнены операции.

Преобразование целых чисел из одной системы счисления в другую. Задача преобразования из СС с основанием q в CC с основанием r сводится к нахождению цифр bi - коэффициентов многочлена b0+qb1+q2b2+...+qnbn из уравнения b0+qb1+q2b2+...+qnbn = c0+rc1+r2c2+...+rnck, где c0, c1, c2, ck - цифры записи числа в исходной СС. Предположим, что мы можем производить арифметические действия в исходной СС. Представим число A, которое надо перевести, в виде схемы Горнера: A=b0+q(b1+q(b2+...+qbn)...). Видно, что при делении A на q в качестве результата получаем b1+q(b2+...+qbn)..., а в качестве остатка - младшую цифру b0 числа A в q-ичной СС. Разделив результат на основание q, получаем в остатке b1 - вторую цифру и так далее, пока в результате не получится ноль. См. примеры перевода из десятичной СС в двоичную, восьмеричную и шестнадцатеричную СС (далее) . Предположим теперь, что требуется перевести число A=c0+qc1+q2c2+...+qncn из q-ичной СС в СС с основанием qm. Преобразуем многочлен: A=(c0+qc1+q2c2+...+qm-1cm-1) + qm(cm+qc1+m+q2c2+m+...+qm-1c2m-1) + q2m(c2m+qc1+2m+q2c2+2m+...+qm-1c3m-1) + ... + qpm(cpm+qc1+pm+q2c2+pm+...+qn-pmcn), где p - наибольшее целое число, при котором pm<n. Мы получили запись числа A в СС с основанием qm с p цифрами, где каждая цифра получается из m цифр исходной записи по формуле: bi=cim+qc1+im+q2c2+im+...+qm-1cm-1+im, bp=cpm+qc1+pm+q2c2+pm+...+qn-pmcn.

Примеры перевода из десятичной СС в двоичную, восьмеричную и шестнадцатеричную СС Двоичная СС (q=2). Переведем число 2310 в двоичное представление. Используя вышеизложенное правило, разделим число 23 на основание целевой СС - 2: 23/2 = 11 и 1 в остатке. Младшая цифра двоичного числа - 1. Делим 11 на 2, получаем 5 и 1 в остатке. Следующая цифра числа - тоже 1. Записываем ее слева от предыдущей цифры - 11. Далее получаем 2 и 1 в остатке, а само число - 111. Далее, 2/2 = 1 и 0 в остатке. Получилось число 0111. Последнюю единицу делим опять на 2, получаем в результате 0 (это значит, что процесс перевода закончен) и в остатке - 1. Получили число 10111. Таким образом, 2310=101112. Восьмеричная СС (q=8). Переведем десятичное число 100 в восьмеричный вид:100/8=12 и 4 в остатке12/8=1 и 4 в остатке1/8=0 и 1 в остаткеПолучили 10010=1448. Шестнадцатеричная СС (q=16). Переведем десятичное число 1000 в шестнадцатеричную СС:1000/16=62 и 8 в остатке62/16=3 и 14 в остатке3/16=0 и 3 в остаткеВспомним, что цифры, большие девяти, обозначаются буквами. Цифре 14 соответствует буква E. Получили 100010=3E816.

Так, чтобы перевести число из двоичной записи в восьмеричную, нужно сгруппировать его цифры по три (23=8). Из каждой триады получается одна восьмеричная цифра. Например, дано число 101110112=10.111.011. Младшая цифра восьмеричной записи будет равна 1+2*1+4*0=3. Средняя 1+1*2+1*4=7, и старшая 0+1*2=2. Получаем 2738. Для перевода из СС с основанием qm в q-ичную СС каждая цифра переводится в q-ичную систему, затем эти цифры записываются по порядку, причем каждая цифра, кроме старшей, дополняется слева нулями до m разрядов. Например, переведем число 2F516 в двоичную СС. В данном случае m=4. Так как 216=102, F16=11112, 516=01012, то 2F516=10111101012.

Перевод правильных дробей из одной системы счисления в другую Правильной дробью называется число, равное m/n, где m и n - натуральные числа, причем m<n. Правильную дробь A в q-ичной системе счисления можно представить в виде A=a1q-1+a2q-2+a3q-3+... аnq-n(1). Не всегда дробь можно представить с абсолютной точностью в виде конечной записи (1), поэтом в задачах заранее указывается максимальное требуемое количество знаков после запятой n. Очевидно, что если умножим A на q, в целой части получим старший разряд a1, а в дробной части - сумму a2q-1+a3q-2+... anq-n+1. Умножая далее еще раз на q, получим следующие цифры ai. Если правила выполнения арифметических действий в исходной СС удобны (например, число представлено в привычной десятичной форме), то перевод в q-ичную СС сводится к нахождению цифр ai, т.е. к последовательному умножению дроби на q и выписыванию по порядку целой части результата. После каждого умножения целая часть обнуляется и операция повторяется n раз. См. пример перевода правильной дроби из десятичной в двоичную, восьмеричную и шестнадцатеричную СС (далее). Если в целевой СС арифметические операции выполнять удобнее (например, требуется перевести в десятичную запись), то вычислять нужно непосредственно по формуле (1). Причем каждая из цифр ai и веса разрядов qi записываются в целевой СС.

Пример перевода правильной дроби из десятичной в двоичную, восьмеричную и шестнадцатеричную СС Двоичная СС (q=2). Переведем число 0.2310 в двоичное представление с абсолютной точностью. Используем вышеизложенное правило: умножим число 0.23 на основание целевой СС - 2: 0.23*2 = 0.46. Видим, что целая часть получившегося числа равна нулю. Значит и первая цифра двоичной дроби - 0. Записываем ее после запятой - 0.0. Умножаем 0.46 еще раз на 2, получаем 0.92. Следующая цифра двоичной дроби - тоже 0. Записываем ее справа от предыдущей цифры - 0.00. Далее получаем 0.92*2=1.84, а само число - 0.001. Далее, обнуляем целую часть и снова умножаем: 0.84*2=1.68. Продолжаем этот процесс:


В конце концов получим число 0.92, которое уже встречалось. Следующие вычисления с этого момента будут периодически повторяться. Повторяющаяся часть дроби (период) выделен скобками в таблице. Таким образом, 0.2310=0.00(11101011100001010001)2. Восьмеричная СС (q=8). Правила перевода дроби в восьмеричное представление аналогичны правилам перевода в двоичную СС. Только умножать надо на 8, а не на 2. Перевдем десятичное число 0.1 в восьмеричный вид с точность до трех цифр после запятой:0.1*8=0.8 - цифра 0 в результате0.8*8=6.4 - следующая цифра результата - 60.4*8=3.2 - цифра 3Получили 0.110 » 0.0638. Шестнадцатиричная СС (q=16). Перевдем десятичное число 0.9 в шестадцатиричную СС с точностью до двух символов после запятой:0.9*16=14.4 - цифра 14 (E) в результате0.4*16=6.4 - следующая цифра результата - 6Получили 0.910 » 0.E616.

Двоичное умножение Наиболее просто операция умножения производится при применении прямого кода. В машинах она реализуется в два этапа. 1-й этап - определяется знак произведения при помощи сложения знаковых цифр по модулю 2. 2-й этап - производится перемножение модулей сомножителей, затем в случае необходимости округление полученного модуля произведения, после чего к модулю результата приписывается его знак, определенный на первом этапе. В машинах может быть реализовано как умножение, начинающееся с младшей цифры (наиболее привычный способ), так и умножение, начинающееся со старшей цифры. При умножении вручную в первом случае частичные произведения сдвигаются влево, во втором - вправо. Оба способа покажем на примере. Пример. Перемножить числа X 1пр. = 0,1010 и X 2пр. = 1,1101.1-й этап - знак произведения 1+1 = 1.2-й этап - перемножаем модули:

В машинах нельзя просуммировать сразу n частичных произведений, как это обычно делает человек. Любой сумматор, как правило, рассчитан на одновременное сложение только двух операндов. Поэтому частичные произведения складываются не сразу, а накапливаются в регистре. При этом полную сумму (произведение) можно получить двумя путями: сдвигом множимого влево при первом способе и вправо при втором; сдвигом суммы частичных произведений на каждом шаге на один разряд вправо при первом способе и влево - при втором. Таким образом, в машинах могут быть реализованы 4 схемы умножения: 1-й вариант - умножение младшими разрядами вперед со сдвигом множимого влево (обычный школьный метод); 2-й вариант - умножение младшими разрядами вперед со сдвигом накапливаемой суммы частичных произведений вправо; 3-й вариант - умножение старшими разрядами вперед со сдвигом множимого вправо; 4-й вариант - умножение старшими разрядами вперед со сдвигом накапливаемой суммы частичных произведений влево.



























