Презентация на тему: Решение задач оптимизации в MS Excel

Решение задач оптимизации в MS Excel ГБОУ Центр образования № 133 Невского районаавт. Баринова Е.А.

Для решения задач оптимизации необходимо:Задать целевую функцию Создать математическую модель задачиРешить задачу на компьютере

Математическая модельМатематическая модель – это приближенное описание какого-либо класса явлений средствами математической символики. При составлении математической модели решения задачи оптимизации искомые величины принимаются за неизвестные и составляется система неравенств, наиболее полно характеризующих решение поставленной задачи. В любую математическую модель входят две составляющие:Ограничения, которые устанавливают зависимости между переменными.Граничные условия показывают, в каких пределах могут быть значения искомых переменных в оптимальном решении.

ЗадачаКомпания производит полки для ванных комнат двух типов - А и В. Агенты по продаже считают, что за неделю на рынке может быть реализовано до 550 полок. Для каждой полки типа А требуется 2 м2 материала, для полки типа В - 3 м2 материала. Компания может получить до 1200 м2 материала в неделю. Для изготовления одной полки типа А требуется 12 мин. работы оборудования, а для изготовления одной полки типа В - 30 мин. Оборудование можно использовать 160 час. в неделю. Если прибыль от продажи полок типа А составляет 3 долл., а от полок типа В - 4 долл., то сколько полок надо выпускать в неделю, чтобы получить максимальную прибыль?

Целевая функцияОчевидно, что в качестве критерия оптимизации в данном случае выступает функция прибыли. Оптимальным будет считаться тот из вариантов решения, в котором значение прибыли будет максимальным. Учитывая, что «…прибыль от продажи полок типа А составляет 3 долл., а от полок типа В - 4 долл.…» целевая функция будет выглядеть следующим образом:3x1 + 4x2 max, где x1 – объем производства полок типа Ax2 – объем производства полок типа B

Ограничение на объем производства:«…Агенты по продаже считают, что неделю на рынке может быть реализовано до 550 полок…» Очевидно, что совокупный объем производства полок не должен превышать 550 единиц, или, в математическом виде:x1 + x2 550

Ограничение на использование оборудования:«…Для изготовления одной полки типа А требуется 12 мин. работы оборудования, а для изготовления одной полки типа В - 30 мин. Оборудование можно использовать 160 часов в неделю…» На основе этой информации можно сделать вывод, что общее время использования оборудования в рамках данного проекта не должно превышать 160 часов в неделю. Переведя время, необходимое для изготовления одной полки в часы (с целью сопоставимости единиц измерения правой и левой части неравенства) получим:0,2x1 + 0,5x2 160

Ограничение на использование материалов:«…Для каждой полки типа А требуется 2 м2 материала, для полки типа В - 3 м2 материала. Компания может получить до 1200 м2 материала в неделю…» На основе этой информации можно сделать вывод, что общее количество материала, затрачиваемого для реализации данного проекта, не должно превышать 1200 м2:2x1 + 3x2 1200

Граничные условияВ качестве граничных условий в данном примере могут быть использованы следующие утверждения, вытекающие из сути поставленной задачи:Объем производства полок типа А и полок типа В – неотрицательное значение.Объем производства полок типа А и полок типа В – целое число, запишем таким образом:x1, x2 0x1, x2 – целое

Ввод условий задачиВвод условий задачи состоит из следующих основных шагов:Создание формы для ввода данных, необходимых для последующего решения.Ввод исходных данных и зависимостей из математической модели.Указание целевой ячейки (ячейки, в которую введена целевая функция), ввод ограничений и граничных условий в диалоговом окне Поиск решения.

Создание формы для ввода данныхТакая форма должна содержать возможность ввода всех данных, необходимых для решения поставленной задачи:искомых переменных;целевой функции;правой и левой части неравенств, описывающих ограничения, налагаемые на возможные варианты решения поставленной задачи.

Ввод исходных данныхОтметим, что целевая функция и левые части неравенств, определяющих возможные варианты решения поставленной задачи, вводятся формулой, в которой роль искомых переменных играют адреса ячеек, зарезервированных для вывода их значений после решения задачи, а роль коэффициентов – адреса ячеек, содержащих соответственные коэффициенты.

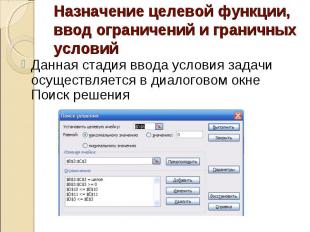
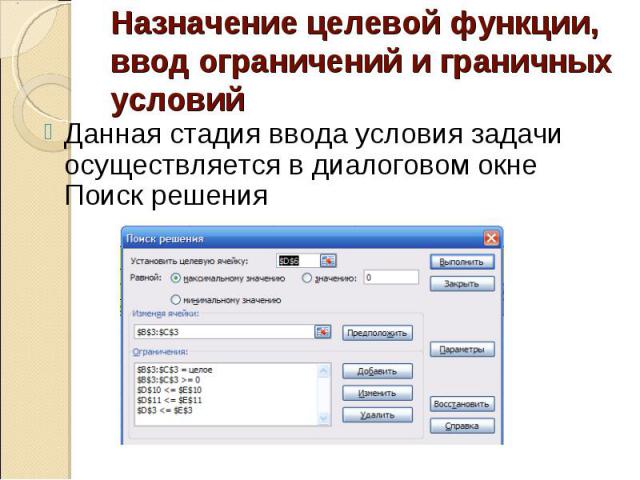
Назначение целевой функции, ввод ограничений и граничных условийДанная стадия ввода условия задачи осуществляется в диалоговом окне Поиск решения

Назначить целевую ячейкуДля этого в поле «Установить целевую ячейку:» вводится адрес ячейки, содержащей целевую функцию. Затем устанавливается направление последней – значение, к которому она должна стремиться исходя из условий задачи (минимальное, максимальное, конкретное, задаваемое пользователем).В поле «Изменяя ячейки:» ввести адреса ячеек, зарезервированных для искомых переменных.

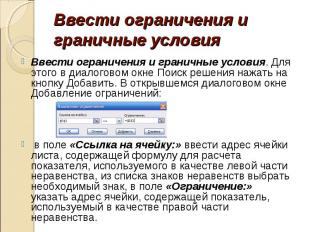
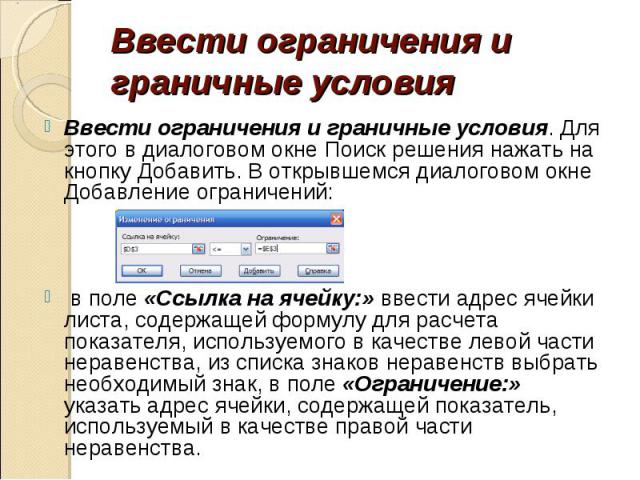
Ввести ограничения и граничные условияВвести ограничения и граничные условия. Для этого в диалоговом окне Поиск решения нажать на кнопку Добавить. В открывшемся диалоговом окне Добавление ограничений: в поле «Ссылка на ячейку:» ввести адрес ячейки листа, содержащей формулу для расчета показателя, используемого в качестве левой части неравенства, из списка знаков неравенств выбрать необходимый знак, в поле «Ограничение:» указать адрес ячейки, содержащей показатель, используемый в качестве правой части неравенства.

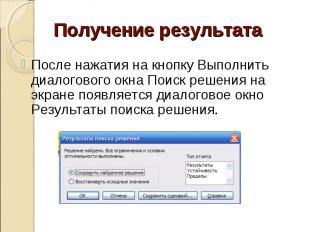
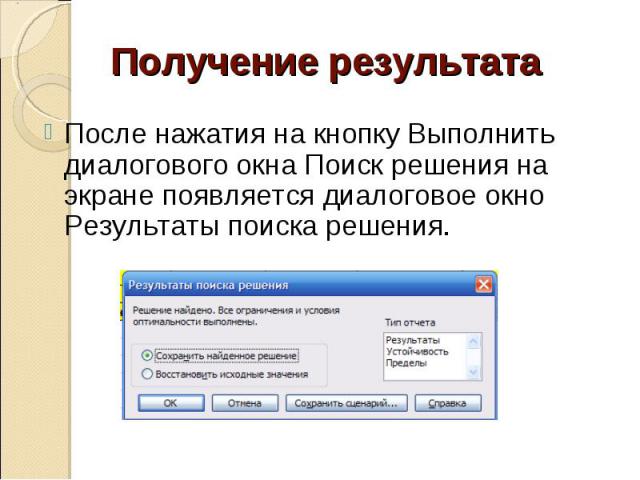
Получение результатаПосле нажатия на кнопку Выполнить диалогового окна Поиск решения на экране появляется диалоговое окно Результаты поиска решения.

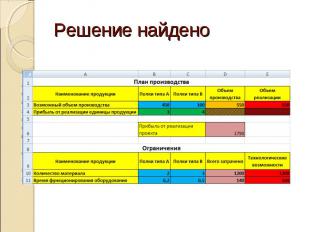
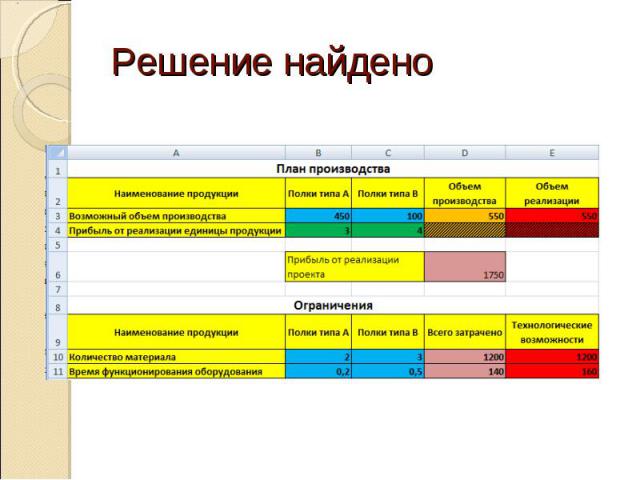
Решение найдено

Оптимальное решение поставленной задачиполок типа А - в количестве 450 штук (В3);полок типа В – в количестве 100 штук (С3).При этом максимальная прибыль будет составлять 1720 единиц, а ресурсы используются следующим образом:потребление материала – 1200 единиц (D10);использование оборудования – 140 часов (D11).