Презентация на тему: MSC.Flightloads 7.1

Цель Расчет реакции на аэродинамическое воздействие – это расчет отклика при воздействии на сбалансированный ЛА малых возмущений. Возмущения могут вноситься приложенными нагрузками или порывом. Отклик может быть временным, гармоническим или случайным.

Ограничения Расчет нагрузки от порыва поддерживается методом Зона51 (сверхзвук) и методом дипольных решеток (дозвук). Всегда необходима модальная редукция. Для восстановления данных применяется метод модальных перемещений. Поддерживается только один расчетный случай. Однако, может быть добавлен расчетный случай для определения собственных частот (ANALYSIS = MODES).

Уравнение динамики В модальных координатах уравнение динамики выглядит как Для аэродинамической нагрузки удобнее иметь дело с уравнением трансформированным в частотную область.

Уравнение динамики для частотной области Преобразование Фурье дает нам следующее уравнение где набегающий поток.

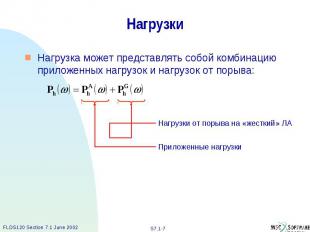
Нагрузки Нагрузка может представлять собой комбинацию приложенных нагрузок и нагрузок от порыва:

Вертикальный порыв: формулировка Нормальный поток, вызванный порывом, на j- ю аэродинамическую панель может быть записан как где

Нагрузка от вертикального порыва на «жесткий» ЛА Преобразование Фурье для нормального обтекания Отсюда, нагрузка от вертикального порыва на «жесткий» ЛА где

Боковой порыв В MSC.Nastran поддерживается только плоский вертикальный порыв, действующий в направлении оси z аэродинамической СК. Моделирование бокового порыва, Необходимо повернуть аэродинамическую СК вокруг оси х, так что бы направление оси z совпало с направлением действия порыва. Установить знавение команды AESYMXZ в ASYMMETRIC Установить значение команды AESYMXY в ANTISYMMETRIC Метка ORIENT объекта PAERO2 должна быть установлена в соответствии с изменением аэродинамической СК

Расчет частотного отклика Этот рачет может быть применен для всех видов расчета реакции на аэродинамическое воздействие. Динамическое уравнение в частотной области решается для заданных пользователем частот. Аэродинамические матрицы предварительно вычисляются для набора приведенных частот, определенных пользователем и необходима интерполяция для рабочих частот.

Расчет частотного отклика : результаты Решением динамического уравнения в частотной области являются модальные перемещения Uh( ). Физические перемещения Ug( ) находятся методом модального суммирования. При желании можно получить остальные результаты: Скорости и ускорения Силы, напряжения, деформации и т.д. Силы на аэродинамических панелях

Расчет частотного отклика: Комбинированный вертикальный и боковой порыв JAR 25.427 в соответствии с FAA 25.427 определяют направление порыва в расчетах по часовой стрелке В соответствии с этим, требуются расчеты в MSC.Nastran раздельного вертикального и бокового порыва, которые могут быть скомбинированы при заключительной обработке результатов. Для порыва под углом суммарная реакция находится как Угол максимальной суммарной реакции вычисляется как Модуль суммарной реакции

Расчет отклика на случайное воздействие При расчете отклика на случайное воздействие вычисляется спектральная плотность энергии реакции в зависимости от спектральной плотности энергии возбуждения Матрица перехода получается из расчета частотного отклика Таким образом, расчет отклика на случайное воздействие является следствием расчета частотного отклика

Расчет отклика на случайное воздействие : выходные данные Могут быть получены: график xy спектральной плотности энергии и автокорреляционная функция. Среднеквадратичное действующее значение и мнимая частота печатаются в файле .f06. Автокорреляционная функция : Среднеквадратичное действующее значение : Средняя частота:

Случайный порыв В MSC.Nastran доступны спектр порыва Вон-Кармана (von Karman) и Драйдена (Dryden) : где v2 среднеквадратичное значение скорости порыва L масштаб турбулентности v0 средняя скорость p = 1/3 (для модели Вон-Кармена) или 1/2 (для модели Драйдена) k = 1.339 (для модели Вон-Кармена) или 1.0 (для модели Драйдена)

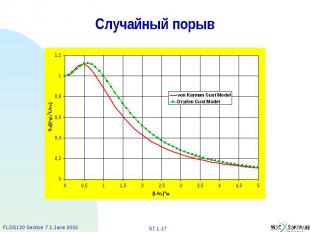
Случайный порыв

Объект TABRNDG из Bulk Data Объект TABRNDG задает случайный порыв: Пример:

Расчет отклика на случайное воздействие : комбинированный вертикальный и боковой порыв Допустим, что вертикальная и боковая составляющая турбулентности являются некоррелированным стационарным случайным Гаусовским процессом, таким что спекр в направлении движения часовой стрелки будет Следовательно, среднеквадратичное действующее значение суммарного отклика Средняя частота вычисляется как A и f0 легко расчитываются используя результаты , полученные при двух расчетах в MSC.Nastran

Расчет переходной характеристики Нагрузки задаются во временной область: Для структурных нагрузок в MSC.Nastran используются нагрузки щависящие от времени.. Для нагрузок, обусловленных воздействием порыва – форма порыва, зависящая от времени. Нагрузки в MSC.Nastran преобразуются в частотную область. Отклик расчитывается в частотной области по заданным пользователем частотам. Отклик преобразуется обратно во временную область по заданному пользователем времени.

Преобразование Фурье Преобразование Фурье производится аналитически. Обратное преобразование Фурье для отклика производится численным методом, основанном на частотном отклике по заданным пользователем частотам. В MSC.Nastran не используется быстрое преобразование Фурье, для того что бы не было ограничений по частотам. Это рекомендует использовать эквидистантные частоты.

Руководящие принципы: частоты Задаваемый ряд частот должен перекрывать частотный ряд нагрузок. Шаг частоты f должен удовлетворять выражению где T рассматриваемый временой интервал. Рассматриваемый временной интервал должен достаточным, что бы все реакции стремились к нулю.

Руководящие принципы : область существования преобразования Фурье Преобразование Фурье существует только для функций, которые на бесконечности стремятся к нулю Таким образом, можно быть уверенным, что все интересующие отклики с ростом значения времени стремятся к нулю. Это может потребовать того, что бы фактическая нагрузка следовала за эквивалентной, с противоположным знаком. Эта эквивалентная нагрузка должна быть приложена во времени так, что бы отклик от начальной нагрузки был постоянным по времени.

Руководящие принципы : твердотельные тона Отклик при t = 0 равен площади под функцией преобразования Фурье. Если конструкция имеет твердотельные тона, то отклик соответствующий 0Hz не будет вычислен. Следовательно обратное преобразование Фурье неучитывает возрастающую область, относящуюся к 0Hz. В результате отклик начинается с ненулевого значения. Эта особенность может быть исключена, если эквивалентная нагрузка будет следовать за начальной нагрузкой, таким образом, преобразование Фурье будет начинаться с 0Hz.

Расчет переходной характеристики : выходные данные Стандартные данные включают Перемещения Силы в заделках Силы и напряжения в элементах Распечатываемые данные Недеформированное изображение конструкции Графики XY

Параметры GUSTAERO: по умолчанию = 1 Нагрузка от порыва будет вычисляться толико при GUSTAERO = -1 MACH : по умолчанию число Маха принимает наименьшее значение Вычисляемые аэродинамические матрицы включают параметр MACH, который используется в расчете реакции на аэродинамическое воздействие Q: по умолчанию = 0.0 Скоростной напор будет вычисляться обязательно.Поэтому этот параметр необходим.

Пример 1: расчет отклика на воздействие порыва Executive и Case Control

Пример 1: Bulk Data

Пример 1: Bulk Data

Пример 1: Bulk Data

Пример 2: отклик на управляемую нагрузку В примере используется модель ha144a FSW с поворачивающимся в зависимости от времени оперением, на которой примере будет проведен расчет отклика. Движение задается через особую точку (EPOINT 115) Особая точка связана с шарнирной точкой оперения (grid 90) через элемент DMIG.

Пример 2: Executive и Case Control

Пример 2: Bulk Data

Пример 2: Bulk Data

Конец