Презентация на тему: Электронный мультимедийный плакат "Логика"

Понятие- это форма человеческого мышления, где фиксируются основные, существенные признаки объекта. Любое понятие состоит из двух составляющих: объёма понятия содержания понятия. Объем понятия- это совокупность (множество) предметов, на которое оно распространяется. Содержание понятия- это совокупность основных, существенных признаков объекта

Умозаключение- это форма мышления, с помощью которой из одного или нескольких суждений (посылок) может быть получено новое суждение (заключение).

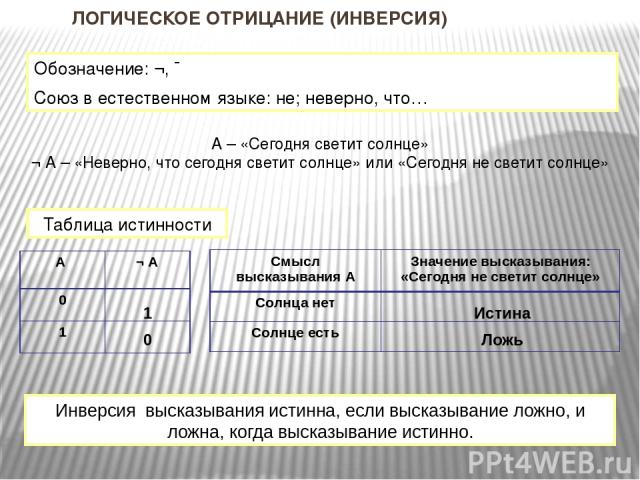
Высказывание- это форма мышления, в которой что-либо утверждается или отрицается о свойствах реальных объектов и отношениях между ними. Высказывание может быть либо истинным, либо ложным. Высказывание не может быть выражено повелительным или вопросительным предложением, т. к. оценка их истинности или ложности невозможна. Высказывания бывают: Общее Частное Единичное Общее высказывание начинается (или можно начать) со слов: все, всякий, каждый, ни один. Частное высказывание начинается ( или можно начать) со слов: некоторые, большинство и т.п. Если высказывание не является частным или общим, то это высказывание является единичным.

Алгебра высказываний Высказывания могут быть простыми или составными. Алгебра высказываний определяет истинность или ложность составных высказываний. Математический аппарат логики: Вводятся вместо простых высказываний логические переменные: А, В, С и т.д. Значения высказываний обозначаются следующим образом: Истина - 1 Ложь - 0 Простое высказывание содержит одну простую мысль. Составные высказывания состоят из простых высказываний и логических операций.

В логике логическими операциями называют действия, вследствие которых порождаются новые понятия, возможно с использованием уже существующих. Логическая операция (логический оператор, логическая связка, пропозициональная связка) — операция над высказываниями, позволяющая составлять новые высказывания путем соединения более простых

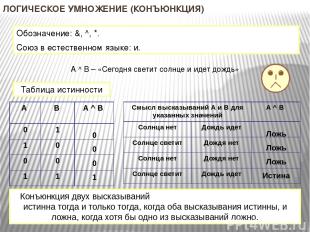
ЛОГИЧЕСКОЕ УМНОЖЕНИЕ (КОНЪЮНКЦИЯ) Обозначение: &, ^, *. Союз в естественном языке: и. А ^ B – «Сегодня светит солнце и идет дождь» 0 0 0 1 Таблица истинности Конъюнкция двух высказываний истинна тогда и только тогда, когда оба высказывания истинны, и ложна, когда хотя бы одно из высказываний ложно. Ложь Ложь Ложь Истина А В А^ B 0 1 1 0 0 0 1 1 Смысл высказываний А и В для указанных значений А^ B Солнца нет Дождь идет Солнце светит Дождя нет Солнца нет Дождя нет Солнце светит Дождь идет

ЛОГИЧЕСКОЕ СЛОЖЕНИЕ (ДИЗЪЮНКЦИЯ) Обозначение: +, V. Союз в естественном языке: или. А V B – На стоянке находится «Мерседес» или «Жигули» Дизъюнкция двух высказываний ложна тогда и только тогда, когда оба высказывания ложны, и истинна, когда хотя бы одно из высказываний истинно. 1 1 0 1 Истина Истина Ложь Истина Таблица истинности А В АVB 0 1 1 0 0 0 1 1 Смысл высказываний А и В для указанных значений АVB «Мерседеса» нет «Жигули» есть «Мерседес» есть «Жигулей» нет «Мерседеса» нет «Жигулей» нет «Мерседес» есть «Жигули» есть

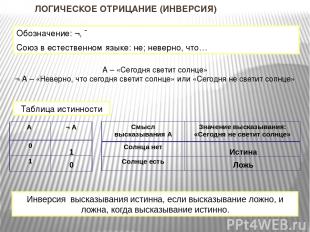
ЛОГИЧЕСКОЕ РАВЕНСТВО (ЭКВИВАЛЕНТНОСТЬ) А – «Число А - четное» В – «Число А кратно 2» А ↔ B – «Число А – четное, тогда и только тогда, когда число А кратно 2» 0 0 1 1 Эквивалентность двух высказываний истинна тогда и только тогда, когда оба высказывания истинны или оба ложны. Ложь Ложь Истина Истина Таблица истинности Обозначение: , , , Союз в естественном языке: тогда и только тогда … А В А ↔B 0 1 1 0 0 0 1 1 Смысл высказываний А и В для указанных значений А ↔B Число нечетное Число кратно 2 Число четное Число не кратно 2 Число нечетное Число не кратно 2 Число четное Число кратно 2

Приоритеты операций Отрицание (не) Конъюнкция (и) Дизъюнкция (или) Импликация (если… , то…) Эквивалентность (тогда и только тогда)

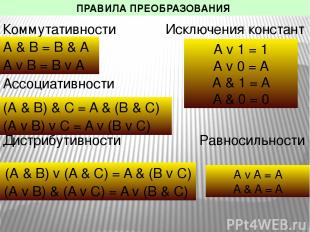
ЗАКОНЫ ЛОГИКИ Закон непротиворечия Закон исключения третьего Закон двойного отрицания Законы де Моргана (законы общей инверсии) А & Ā = 0 А v Ā = 1 А & В = А v В А = A А v В = А & В

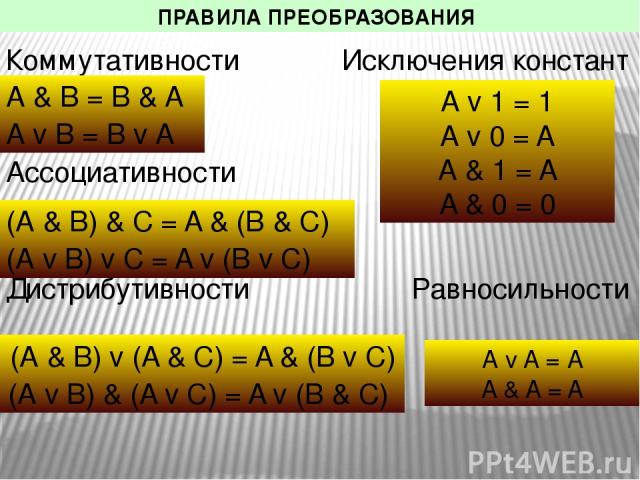
ПРАВИЛА ПРЕОБРАЗОВАНИЯ Коммутативности Исключения констант Ассоциативности Дистрибутивности Равносильности А & В = В & А А v В = В v А (А & В) & C = A & (В & C) (А v В) v C = A v (В v C) (А & В) v (A & C) = A & (В v C) (А v В) & (A v C) = A v (В & C) А v A = А A & A = A А v 1 = 1 А v 0 = A А & 1 = A A & 0 = 0