Презентация на тему: Треугольник

Геометрия Треугольник

Содержание:1) Давайте вспомним.2)Подобные фигуры3)Определение подобных треугольников4)Признаки подобия треугольника5) Это интересно.6) Еще немного о треугольниках.

Давайте вспомним Треугольник- это геометрическая фигура состоящая из трех точек не лежащие на прямой и трех отрезков, попарно соединяющих эти точки. Эти точки называются вершинами треугольника, а отрезки сторонами треугольника.

Подобные фигуры Чем похожи фигуры? ФОРМОЙ!

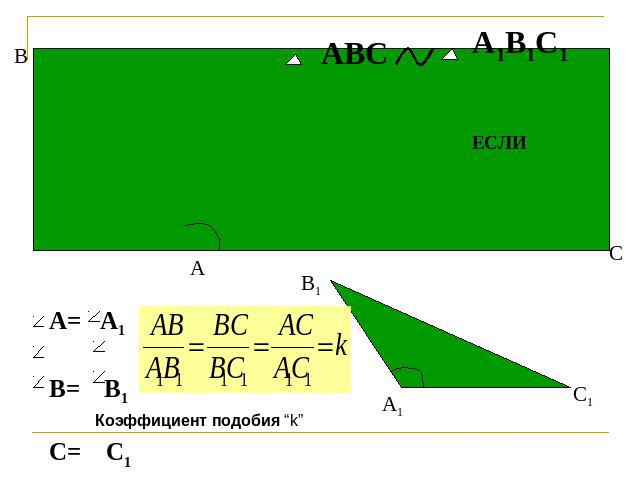
Определение подобных треугольников Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.

Признаки подобия треугольников 1 Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.2 Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.3 Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.

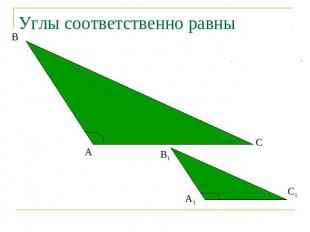
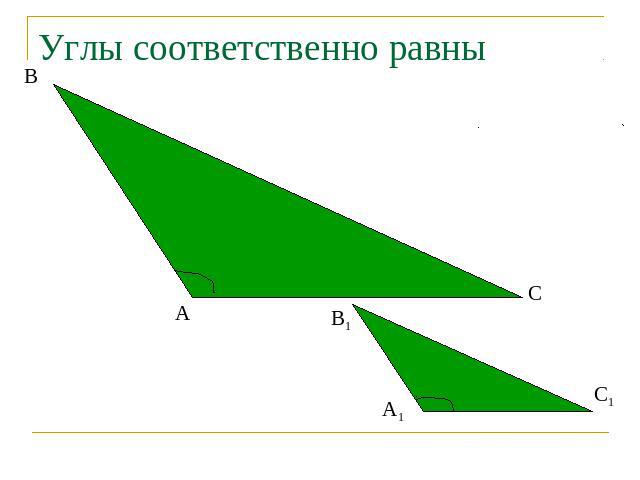
Углы соответственно равны

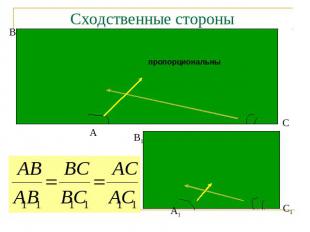
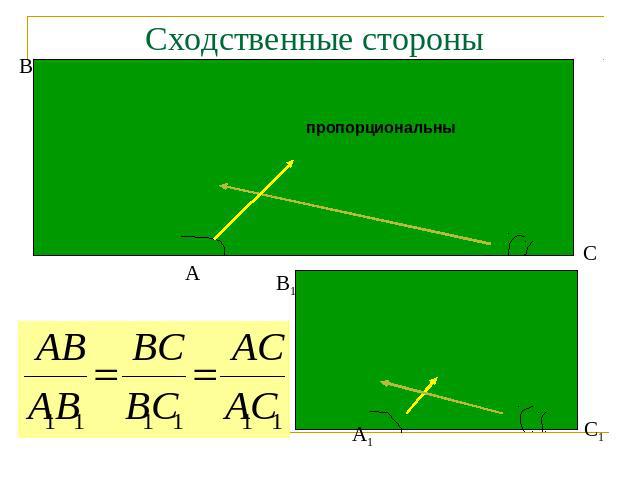
Сходственные стороны

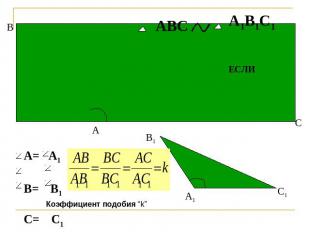
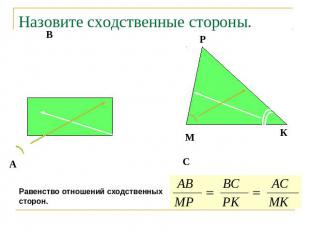
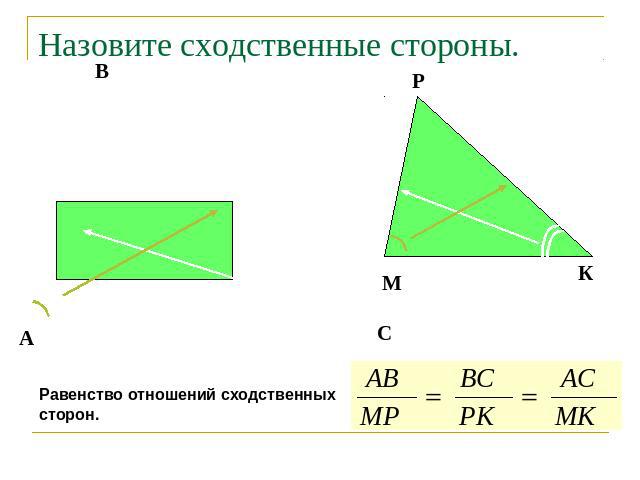
Назовите сходственные стороны.

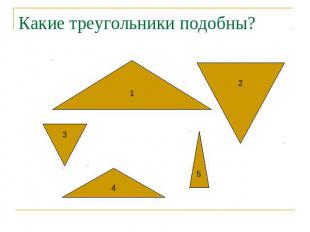
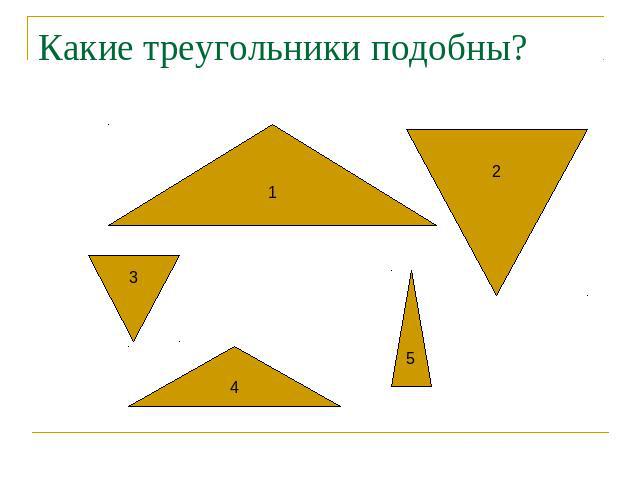
Какие треугольники подобны?

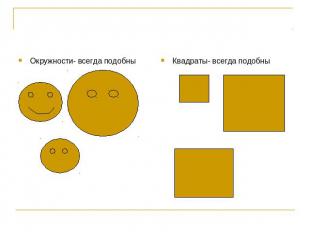
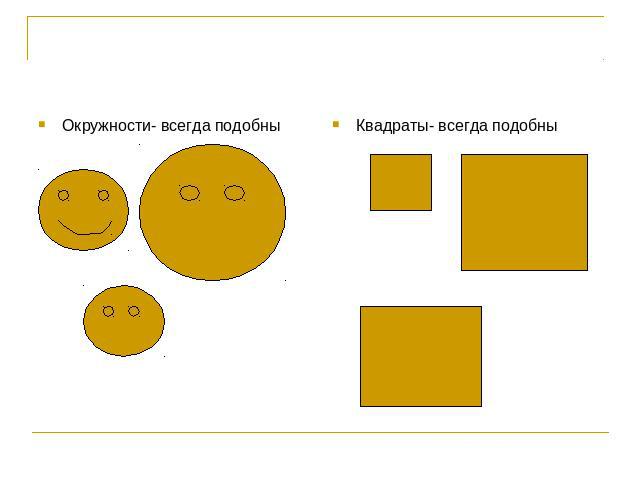
Окружности- всегда подобны Квадраты- всегда подобны

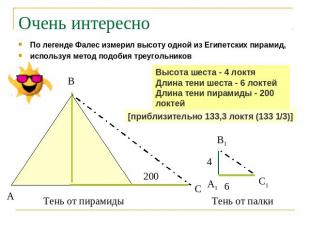
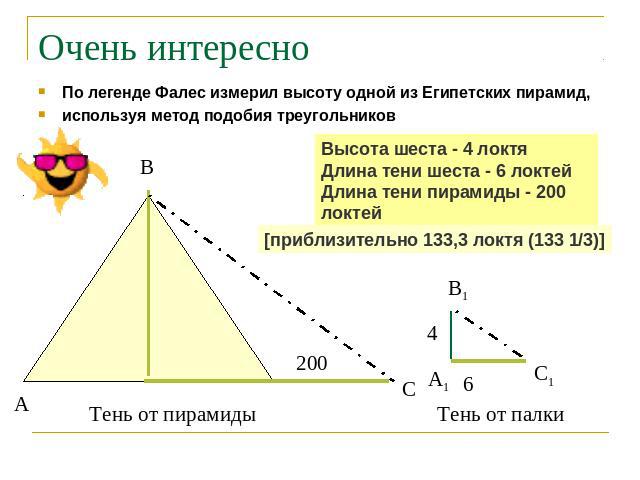
Очень интересно По легенде Фалес измерил высоту одной из Египетских пирамид,используя метод подобия треугольниковВысота шеста - 4 локтяДлина тени шеста - 6 локтейДлина тени пирамиды - 200 локтей

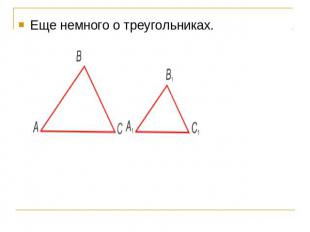
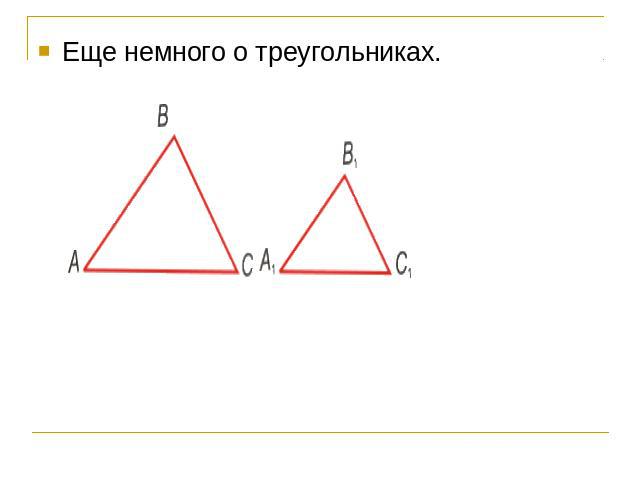
Еще немного о треугольниках.

Пропорциональные отрезки в треугольнике Биссектриса любого внутреннего угла треугольника делит противоположную сторону на части, пропорциональные сторонам треугольника:

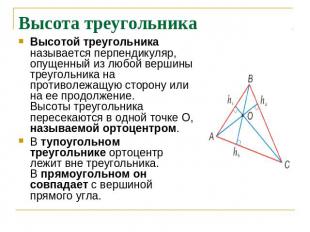
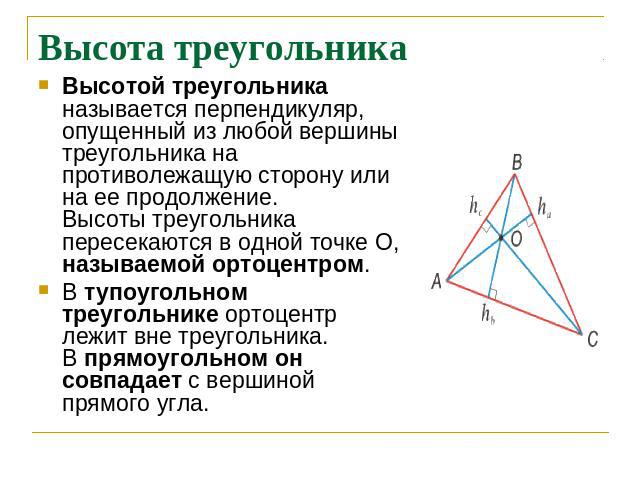
Высота треугольника Высотой треугольника называется перпендикуляр, опущенный из любой вершины треугольника на противолежащую сторону или на ее продолжение.Высоты треугольника пересекаются в одной точке О, называемой ортоцентром.В тупоугольном треугольнике ортоцентр лежит вне треугольника.В прямоугольном он совпадает с вершиной прямого угла.

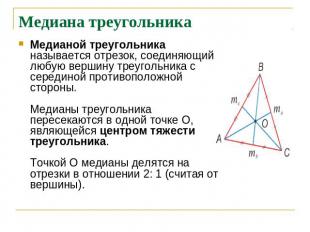
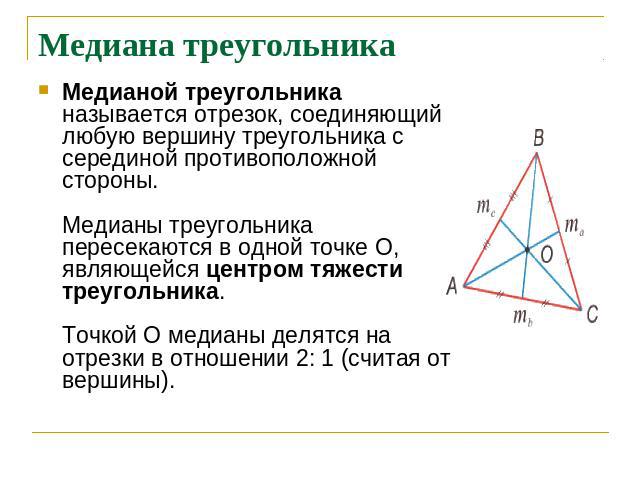
Медиана треугольника Медианой треугольника называется отрезок, соединяющий любую вершину треугольника с серединой противоположной стороны.Медианы треугольника пересекаются в одной точке О, являющейся центром тяжести треугольника. Точкой О медианы делятся на отрезки в отношении 2: 1 (считая от вершины).

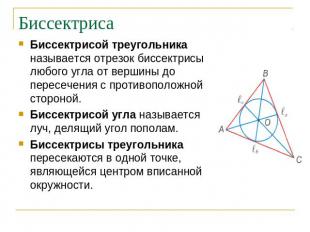
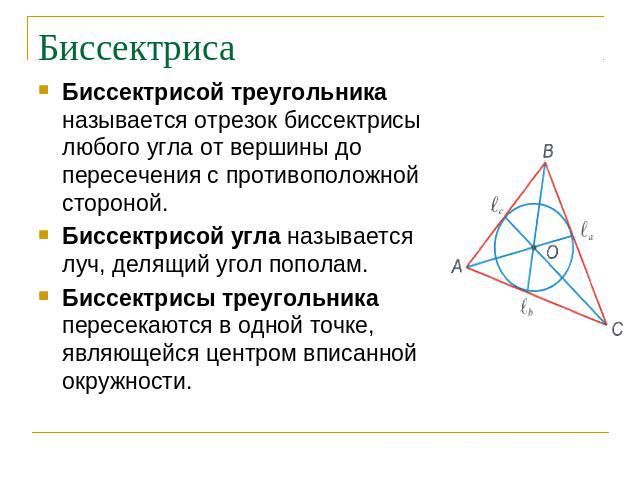
Биссектриса Биссектрисой треугольника называется отрезок биссектрисы любого угла от вершины до пересечения с противоположной стороной.Биссектрисой угла называется луч, делящий угол пополам. Биссектрисы треугольника пересекаются в одной точке, являющейся центром вписанной окружности.

Проект подготовила Ученица 8 Б класса Мертвищева Екатерина СПАСИБО ЗА ВНИМАНИЕ!!!