Презентация на тему: Пространственные фигуры на плоскости

ИЗОБРАЖЕНИЕ ПРОСТРАНСТВЕННЫХ ФИГУР НА ПЛОСКОСТИ Авторы: Баринкова Л.В. Скоробогатова Э.А. 900igr.net

ЦЕЛЬ УРОКА Повторить свойства параллельных прямых и плоскостей, свойства параллельного проецирования, научиться правильно изображать плоские фигуры и объёмные тела на плоскости.

ВЕРНО - НЕВЕРНО ? 1. Верно ли, что через любую точку пространства можно провести множество прямых параллельных данной прямой?

ОТВЕТЫ И ПОДСКАЗКИ Ответ: Неверно. По теореме о существовании прямой, параллельной данной прямой, через точку пространства можно провести единственную прямую.

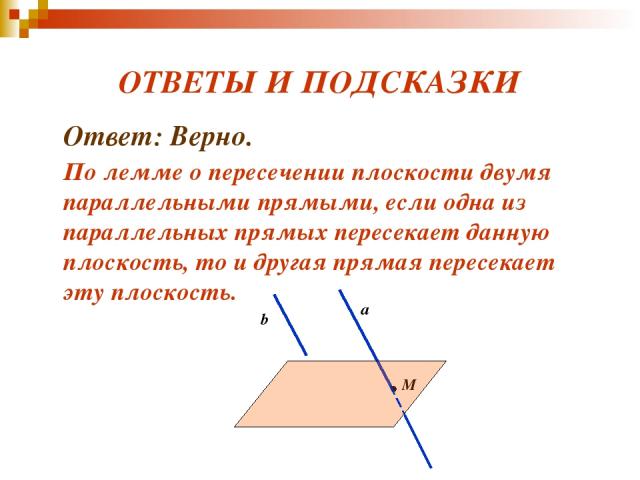
ВЕРНО - НЕВЕРНО ? 2. Верно ли, что если одна из двух параллельных прямых пересекает плоскость, то и другая тоже пересекает эту плоскость?

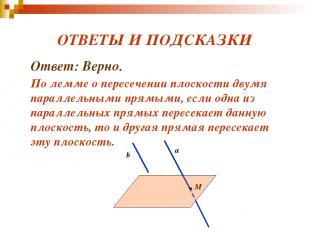
ОТВЕТЫ И ПОДСКАЗКИ Ответ: Верно. По лемме о пересечении плоскости двумя параллельными прямыми, если одна из параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость. b a M

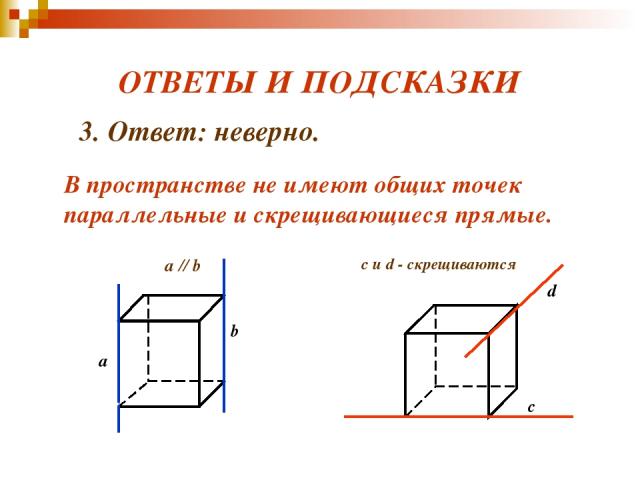
ВЕРНО - НЕВЕРНО ? 3. Верно ли, что две непересекающиеся прямые в пространстве параллельны?

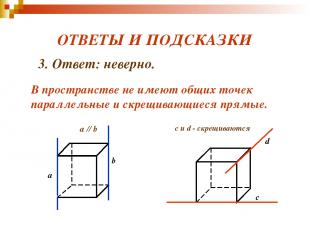
ОТВЕТЫ И ПОДСКАЗКИ с d c и d - скрещиваются 3. Ответ: неверно. В пространстве не имеют общих точек параллельные и скрещивающиеся прямые.

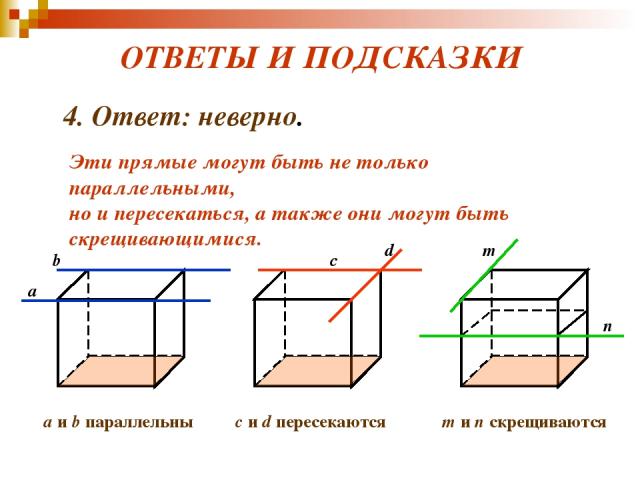
ВЕРНО – НЕВЕРНО? 4. Верно ли, что если две прямые параллельны некоторой плоскости, то они параллельны друг другу?

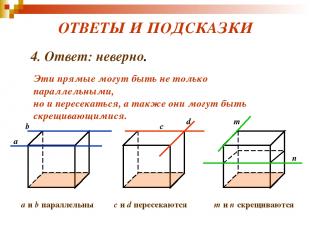
ОТВЕТЫ И ПОДСКАЗКИ 4. Ответ: неверно. Эти прямые могут быть не только параллельными, но и пересекаться, а также они могут быть скрещивающимися. a b c d m n a и b параллельны с и d пересекаются m и n скрещиваются

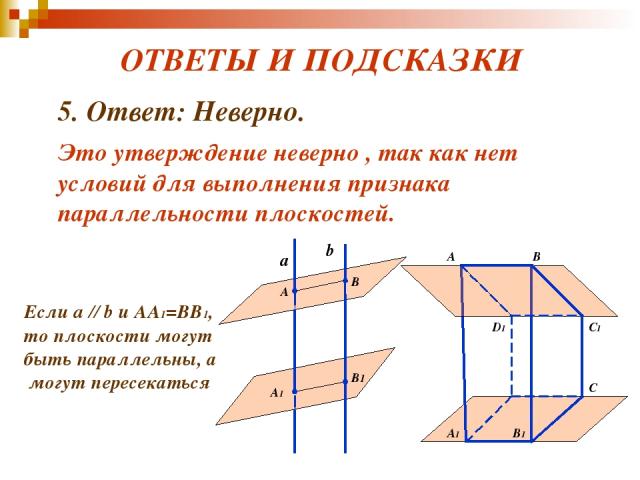
ВЕРНО – НЕВЕРНО? 5. Верно ли, что если две плоскости пересечены двумя параллельными прямыми и отрезки данных прямых, заключённых между ними равны, то плоскости параллельны?

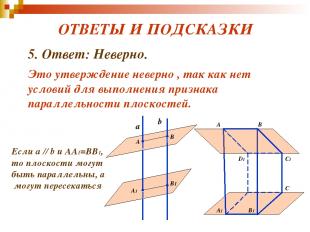
ОТВЕТЫ И ПОДСКАЗКИ 5. Ответ: Неверно. Это утверждение неверно , так как нет условий для выполнения признака параллельности плоскостей. а b А В А1 В1 Если a // b и АА1=BВ1, то плоскости могут быть параллельны, а могут пересекаться А B C1 А1 B1 C D1

ЖЕРАР ДЕЗАРГ (2 марта 1593 – 8 октября 1662) Французский математик. Был военным инженером. Заложил основы проективной и начертательной геометрии. В своих исследованиях систематически применял перспективное изображение. Первым ввёл понятие бесконечно удалённых элементов. В своих сочинениях о резьбе по камню и о солнечных часах Ж.Дезарг дает геометрическое обоснование практическим операциям.

ГАСПАР МОНЖ (10 мая 1746 – 28 июня 1818) Французский математик и общественный деятель, член Парижской академии наук. Профессор Мезьерской военно-инженерной школы Политехнической школы в Париже. Основные интересы учёного лежали в области геометрии. Он создал общий метод изображения пространственных фигур на плоскости, изучал пространственные кривые и поверхности. В1799 году была издана книга «Начертательная геометрия», где он изложил свою теорию. Гаспару Монжу также принадлежат работы по математическому анализу, химии, оптике, метеорологии и практической механике. В 1792-1793 был морским министром, а затем заведовал пороховыми и пушечными заводами республики. Участвовал в Египетской экспедиции Наполеона Бонапарта в 1798-1801. Стал сенатором и графом, но в период Реставрации Монж был лишен всех прав и изгнан из Академии наук.

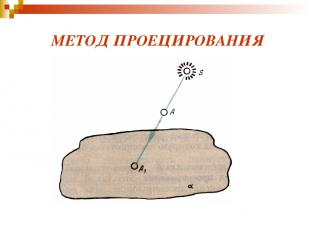
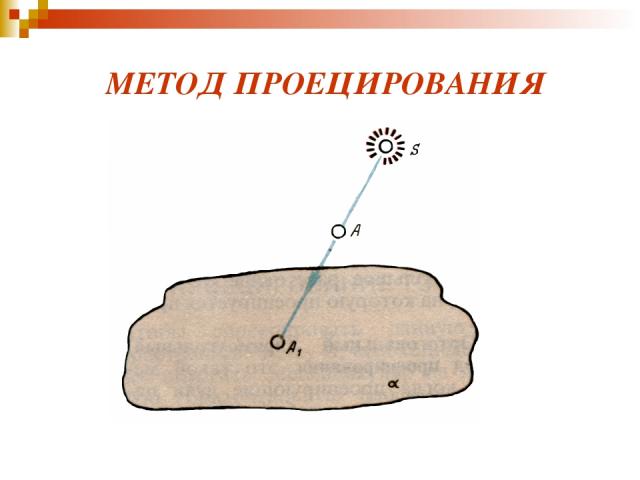
МЕТОД ПРОЕЦИРОВАНИЯ

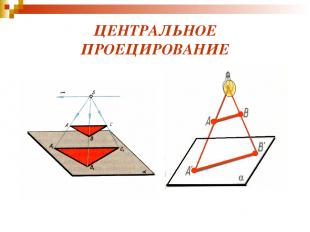
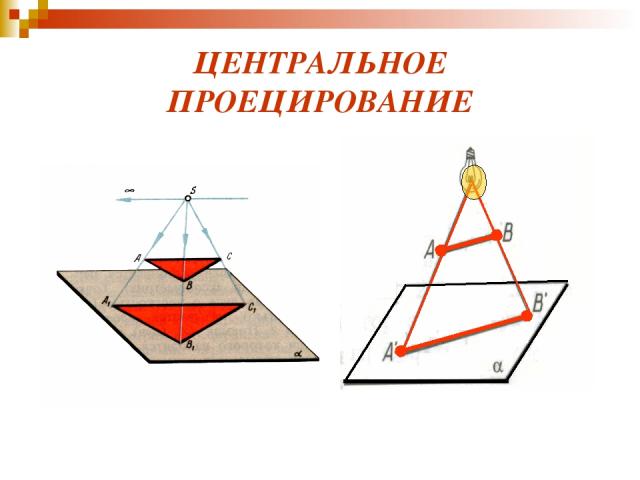
ЦЕНТРАЛЬНОЕ ПРОЕЦИРОВАНИЕ

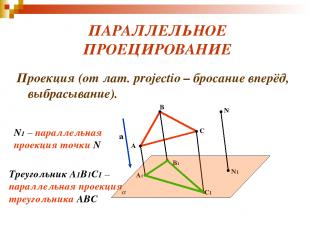
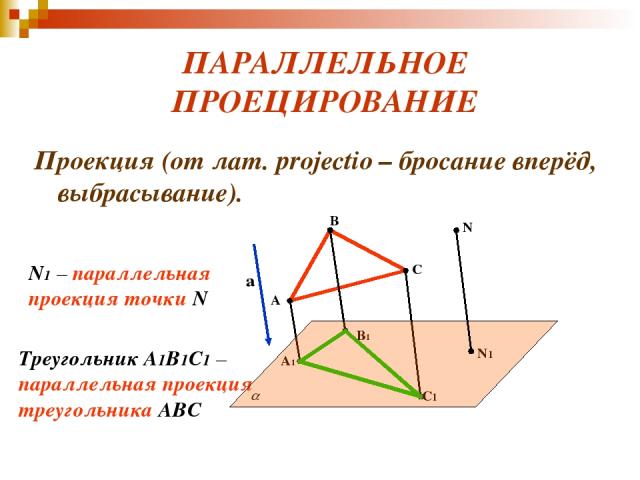
ПАРАЛЛЕЛЬНОЕ ПРОЕЦИРОВАНИЕ Проекция (от лат. projectio – бросание вперёд, выбрасывание). а A B C A1 B1 C1 N N1 N1 – параллельная проекция точки N Треугольник A1B1C1 – параллельная проекция треугольника ABC

ПАРАЛЛЕЛЬНОЕ ПРОЕЦИРОВАНИЕ Параллельную проекцию реальной фигуры представляет, например, её тень, падающая на плоскую поверхность при солнечном освещении, поскольку солнечные лучи можно считать параллельными.

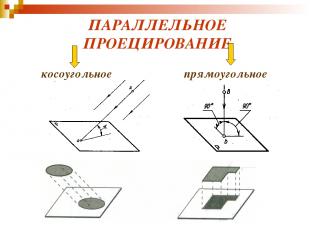
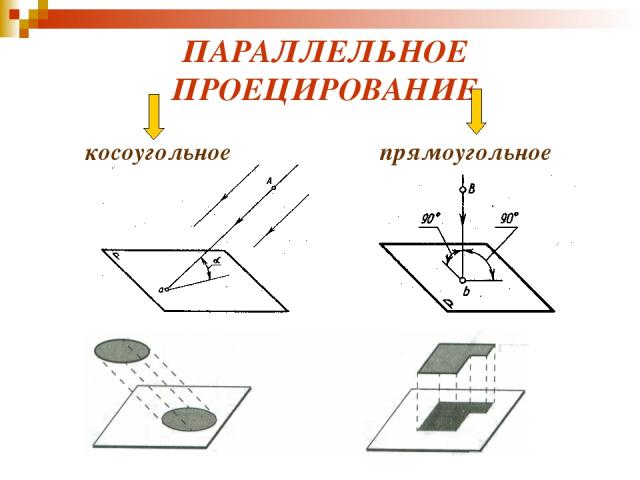
ПАРАЛЛЕЛЬНОЕ ПРОЕЦИРОВАНИЕ косоугольное прямоугольное

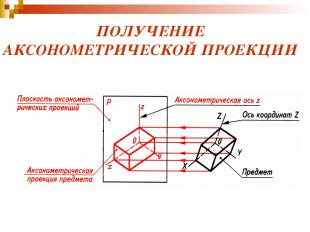
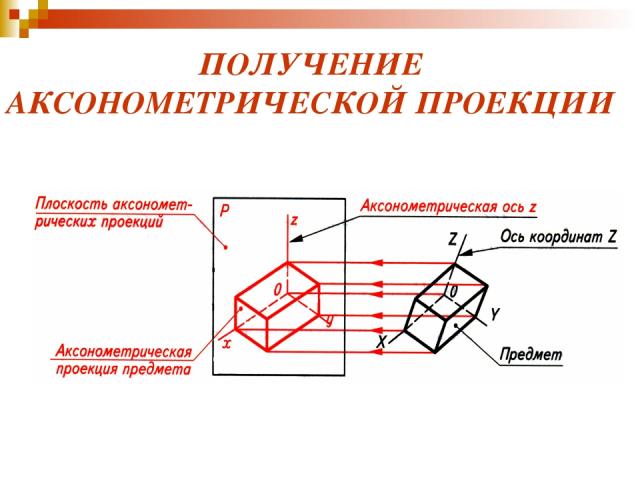
ПОЛУЧЕНИЕ АКСОНОМЕТРИЧЕСКОЙ ПРОЕКЦИИ

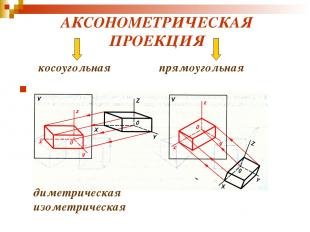
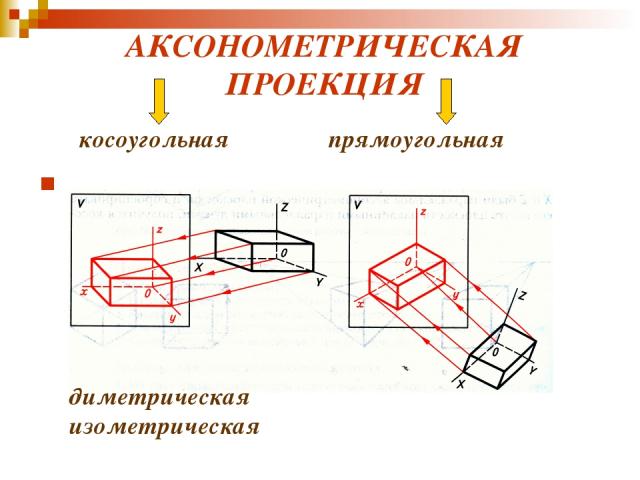
диметрическая изометрическая АКСОНОМЕТРИЧЕСКАЯ ПРОЕКЦИЯ косоугольная прямоугольная

ТЕАТР ТЕНЕЙ

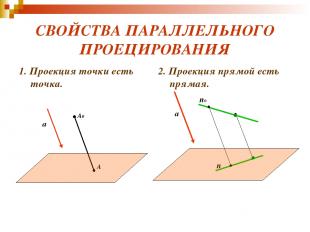
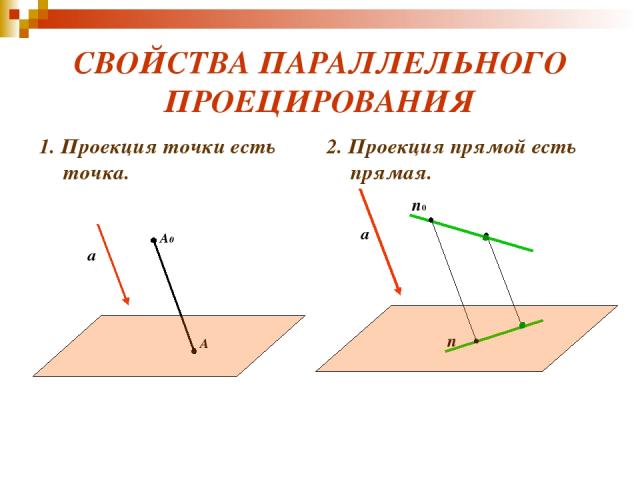
СВОЙСТВА ПАРАЛЛЕЛЬНОГО ПРОЕЦИРОВАНИЯ 1. Проекция точки есть точка. 2. Проекция прямой есть прямая. A0 A a n n0 a

ТЕАТР ТЕНЕЙ

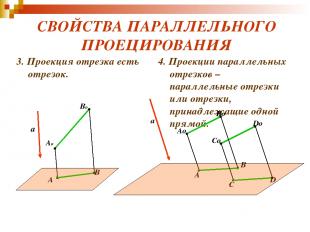
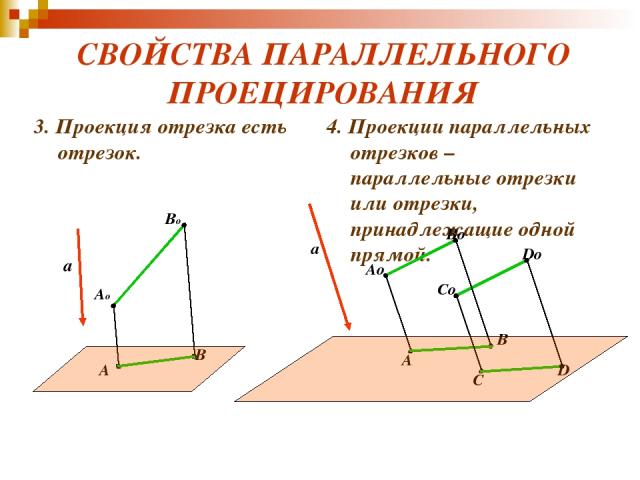
СВОЙСТВА ПАРАЛЛЕЛЬНОГО ПРОЕЦИРОВАНИЯ 3. Проекция отрезка есть отрезок. 4. Проекции параллельных отрезков – параллельные отрезки или отрезки, принадлежащие одной прямой. a Ao Bo A B a Ao Bo A B Co Do C D

ТЕАТР ТЕНЕЙ

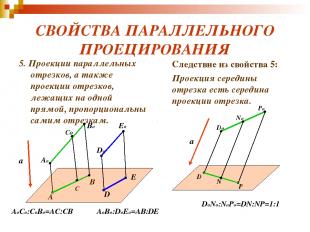
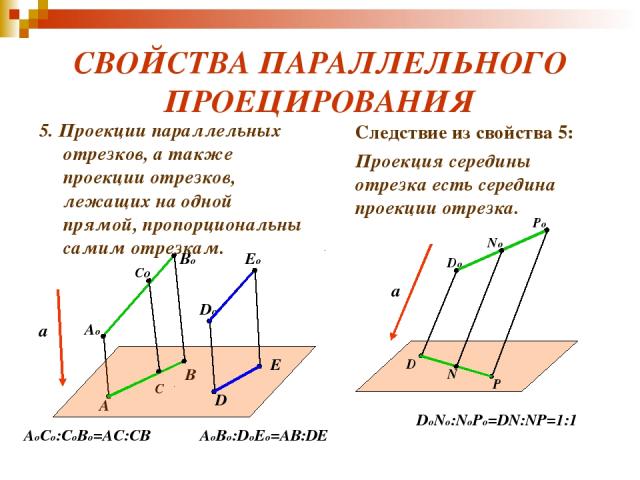
СВОЙСТВА ПАРАЛЛЕЛЬНОГО ПРОЕЦИРОВАНИЯ 5. Проекции параллельных отрезков, а также проекции отрезков, лежащих на одной прямой, пропорциональны самим отрезкам. Следствие из свойства 5: Проекция середины отрезка есть середина проекции отрезка. a Ao Bo A B Co C No Do Po D P N AoCo:CoBo=AC:CB DoNo:NoPo=DN:NP=1:1 a Do Eo D E AoBo:DoEo=AB:DE

ТЕАТР ТЕНЕЙ

СВОЙСТВА ПАРАЛЛЕЛЬНОГО ПРОЕЦИРОВАНИЯ При параллельном проецировании сохраняются следующие свойства фигур 1. Свойство фигуры быть точкой, прямой и плоскостью. 2. Свойство фигур иметь пересечение. 3. Деление отрезка в данном отношении. 4. Параллельность прямых и плоскостей. 5. Свойство фигуры быть треугольником, параллелограммом, трапецией. 6. Отношение длин параллельных отрезков. 7. Отношение площадей двух фигур.

СВОЙСТВА ПАРАЛЛЕЛЬНОГО ПРОЕЦИРОВАНИЯ При параллельном проецировании не сохраняются следующие свойства фигур: 1. Свойство прямых и плоскостей образовывать между собой углы определенной градусной меры (в частности быть взаимно перпендикулярными). 2. Отношение длин не параллельных отрезков. 3. Отношение величин углов между прямыми (в частности, свойство луча быть биссектрисой угла).

ЗАДАЧИ Задача 1. Построить изображение правильного треугольника ABC , изображение высоты BH и биссектрисы АK. Задача 2. Трапеция ABCD – параллельная проекция равнобедренной трапеции. Построить ось симметрии и высоту данной трапеции. Задача 3. Начертите параллельную проекцию ромба АBCD, имеющего угол A= 60. Постройте изображение высоты этого ромба, проведенной из вершины острого угла.

КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Что является параллельной проекцией отрезка, треугольника, прямоугольника, квадрата, окружности? 2. Какие величины не изменяются при параллельном проецировании? (длина отрезка, градусная мера углов, отношения длин отрезков, отношение площадей двух фигур)? 3. Может ли при параллельном проецировании параллелограмма получиться трапеция и наоборот?