Презентация на тему: Прямая и плоскость

ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСТКОСТЕЙ В ПРОСТРАНСТВЕ Выполнила Ученица 10 класса Б МБОУ лицея № 1 Ким Елена 900igr.net

ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ Стереометрия – (от греч. «стереос»- «объемный», «пространственный») раздел геометрии, изучающий форму, размеры и взаимное расположение пространственных фигур. Аксиомы стереометрии 1.) Аксиома выхода в пространство 2.)Аксиома плоскости 3.)Аксиома прямой 4.)Аксиома пересечения плоскостей

АКСИОМА ВЫХОДА В ПРОСТРАНСТВО Аксиома : имеются 4 точки, не лежащие в одной плоскости.

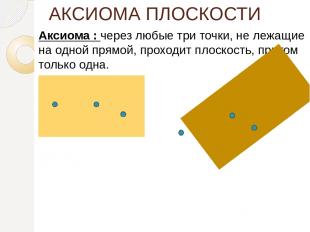
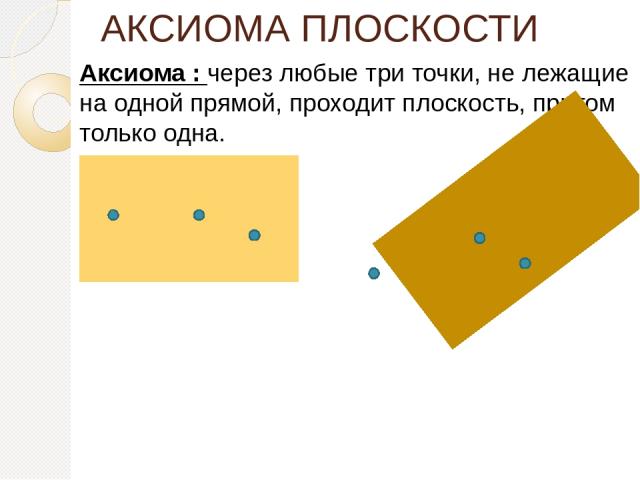
АКСИОМА ПЛОСКОСТИ Аксиома : через любые три точки, не лежащие на одной прямой, проходит плоскость, притом только одна.

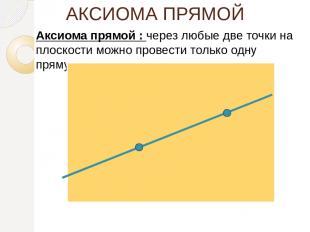
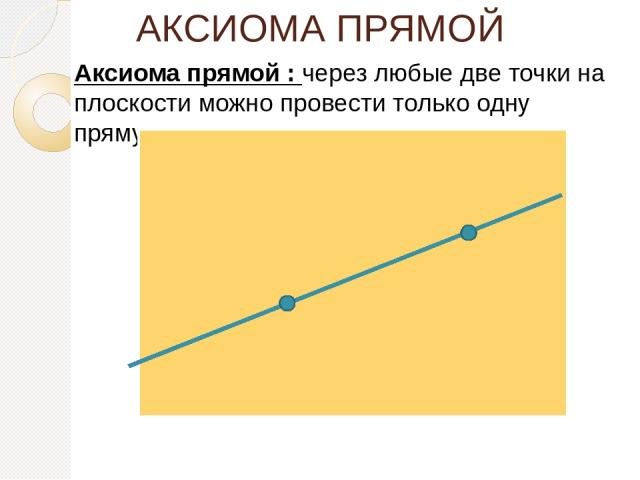
АКСИОМА ПРЯМОЙ Аксиома прямой : через любые две точки на плоскости можно провести только одну прямую.

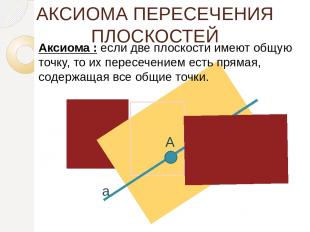
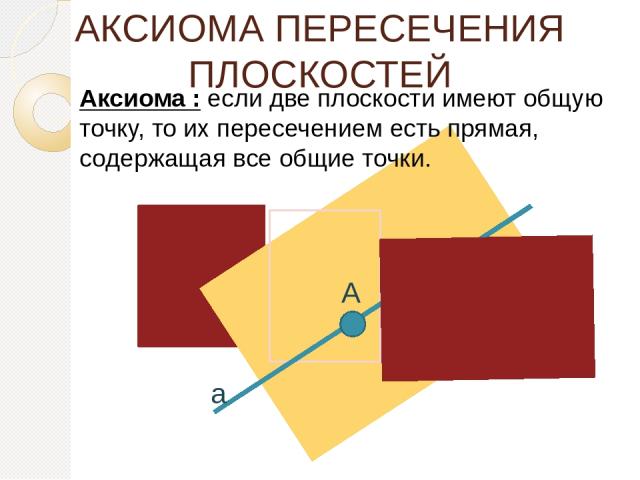
АКСИОМА ПЕРЕСЕЧЕНИЯ ПЛОСКОСТЕЙ Аксиома : если две плоскости имеют общую точку, то их пересечением есть прямая, содержащая все общие точки. a А

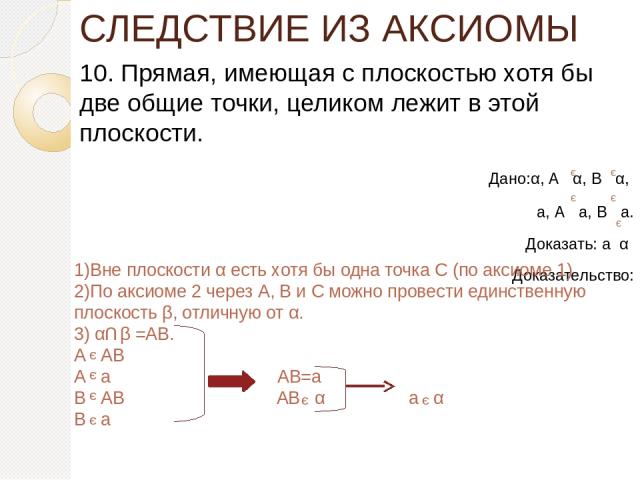
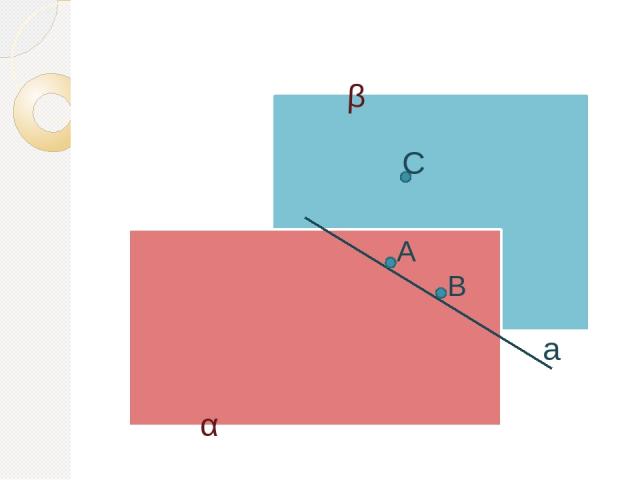
СЛЕДСТВИЕ ИЗ АКСИОМЫ 10. Прямая, имеющая с плоскостью хотя бы две общие точки, целиком лежит в этой плоскости. Дано:α, А α, В α, а, А а, В а. Доказать: а α Доказательство: э э э э э 1)Вне плоскости α есть хотя бы одна точка С (по аксиоме 1) 2)По аксиоме 2 через А, В и С можно провести единственную плоскость β, отличную от α. 3) α β =AB. А АВ А а АВ=а В АВ АВ α а α В а U э э э э э э

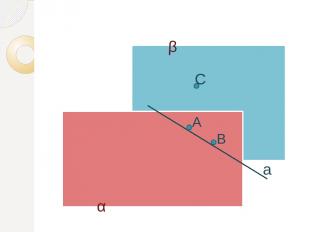
α β С А В а

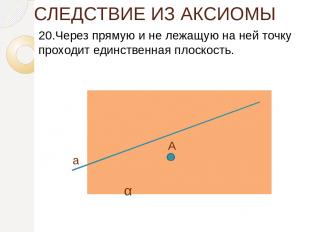
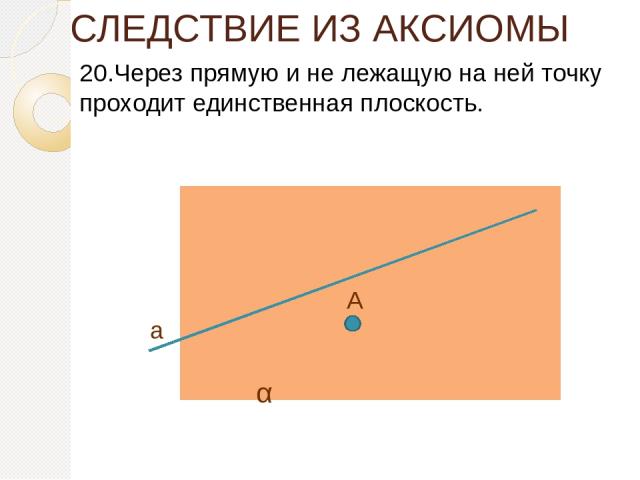
СЛЕДСТВИЕ ИЗ АКСИОМЫ 20.Через прямую и не лежащую на ней точку проходит единственная плоскость. α А а

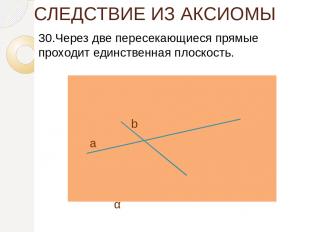
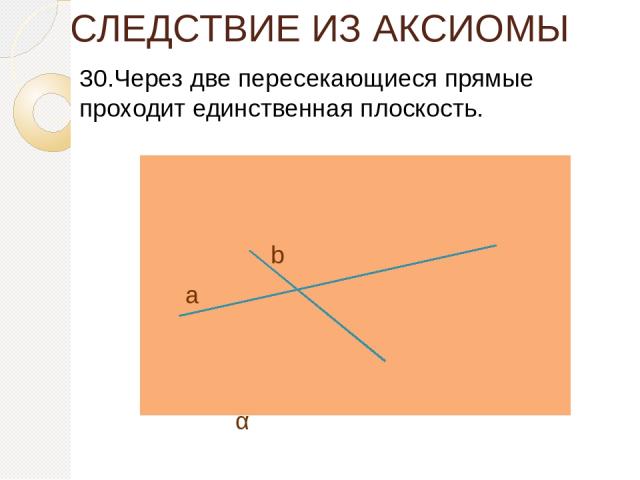
СЛЕДСТВИЕ ИЗ АКСИОМЫ 30.Через две пересекающиеся прямые проходит единственная плоскость. а b α

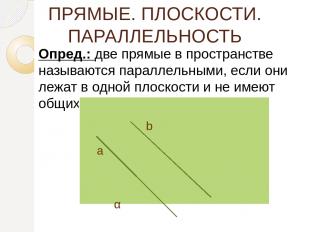
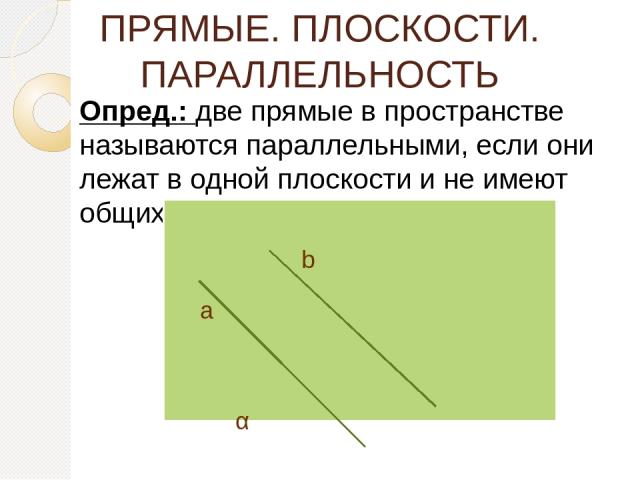
ПРЯМЫЕ. ПЛОСКОСТИ. ПАРАЛЛЕЛЬНОСТЬ Опред.: две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не имеют общих точек. α а b

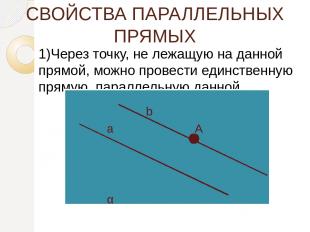
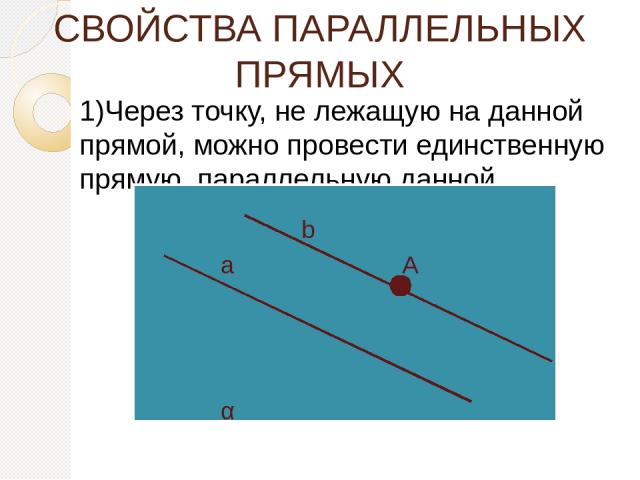
СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ 1)Через точку, не лежащую на данной прямой, можно провести единственную прямую, параллельную данной. α а b А

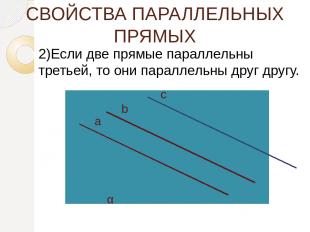
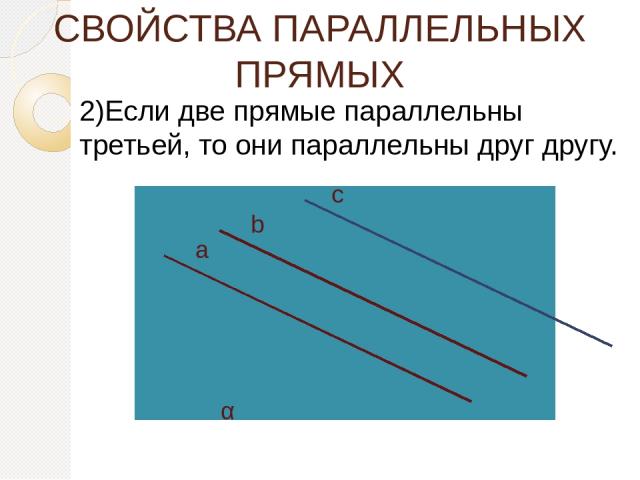
СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ 2)Если две прямые параллельны третьей, то они параллельны друг другу. b а с α

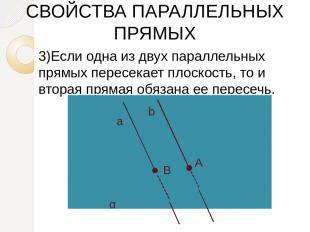
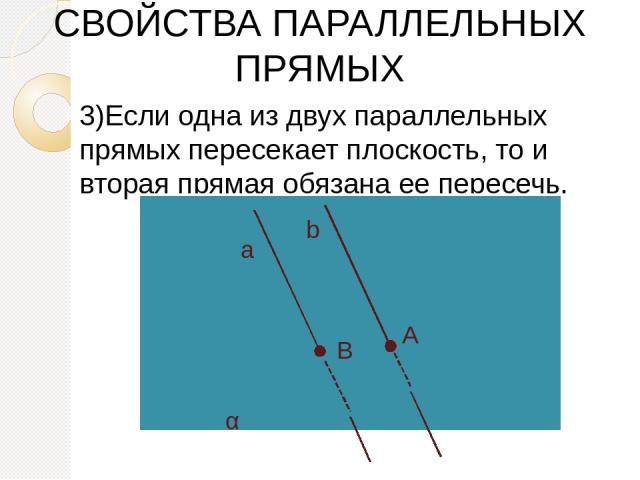
3)Если одна из двух параллельных прямых пересекает плоскость, то и вторая прямая обязана ее пересечь. СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ α а b А В

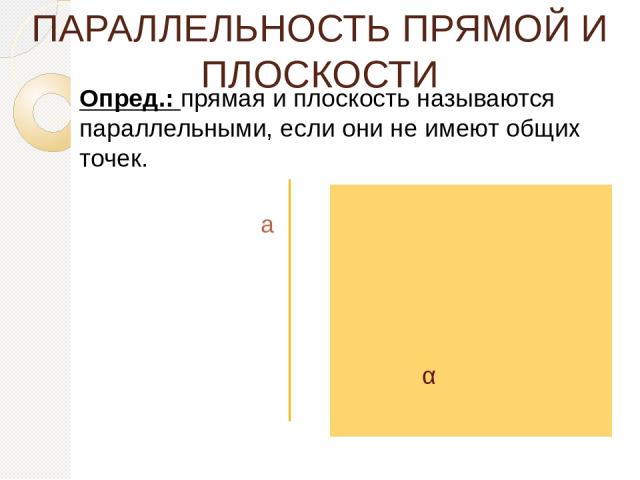
ПАРАЛЛЕЛЬНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ Опред.: прямая и плоскость называются параллельными, если они не имеют общих точек. а α

ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ПРЯМОЙ И ПЛОСКОСТИ Теорема : Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости. а b α

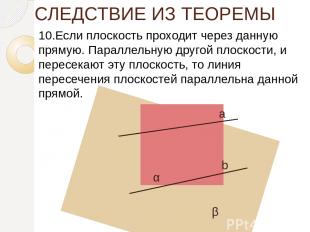
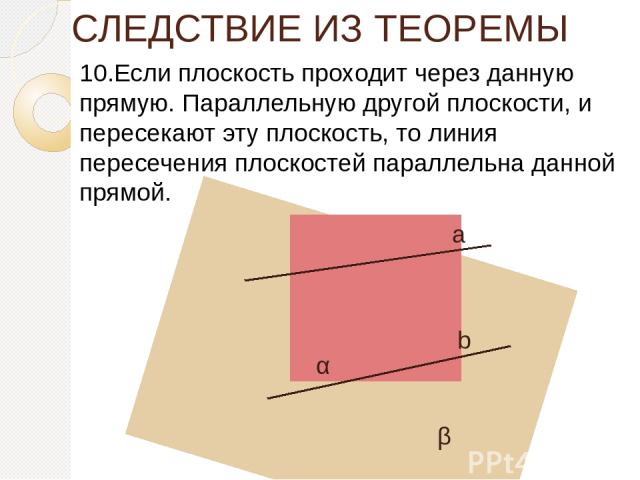
СЛЕДСТВИЕ ИЗ ТЕОРЕМЫ 10.Если плоскость проходит через данную прямую. Параллельную другой плоскости, и пересекают эту плоскость, то линия пересечения плоскостей параллельна данной прямой. а b α β

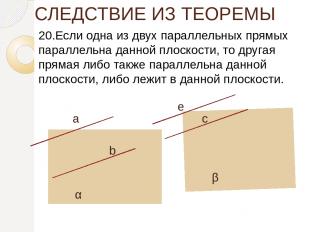
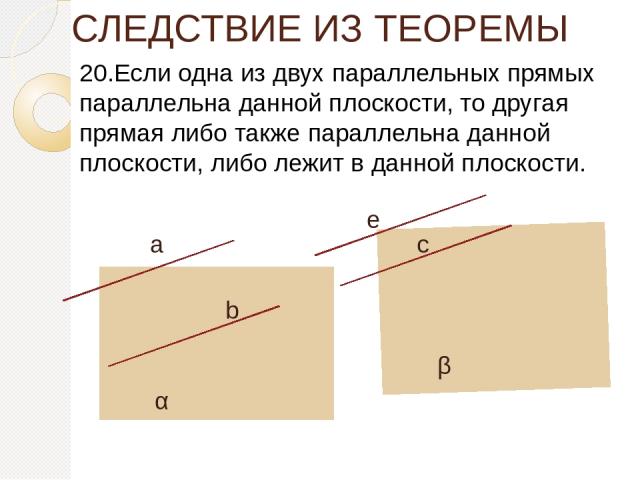
СЛЕДСТВИЕ ИЗ ТЕОРЕМЫ 20.Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в данной плоскости. а b с е α β

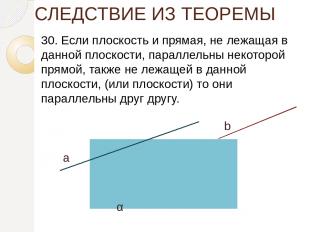
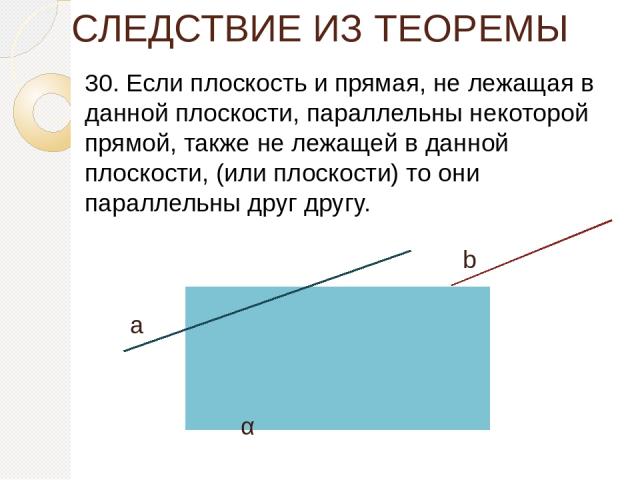
СЛЕДСТВИЕ ИЗ ТЕОРЕМЫ 30. Если плоскость и прямая, не лежащая в данной плоскости, параллельны некоторой прямой, также не лежащей в данной плоскости, (или плоскости) то они параллельны друг другу. а b α

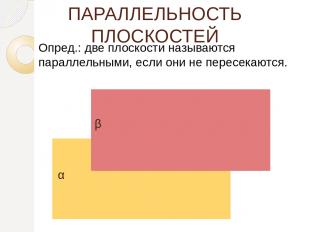
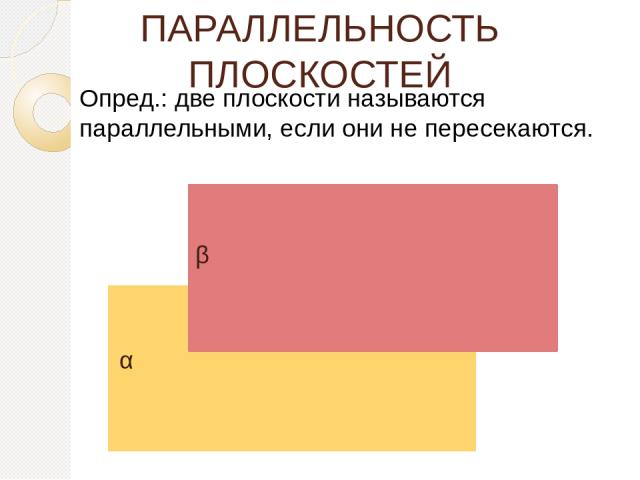
ПАРАЛЛЕЛЬНОСТЬ ПЛОСКОСТЕЙ Опред.: две плоскости называются параллельными, если они не пересекаются. α β

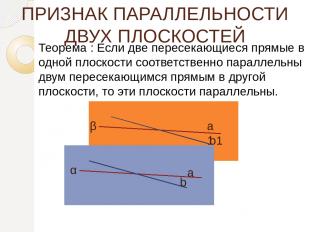
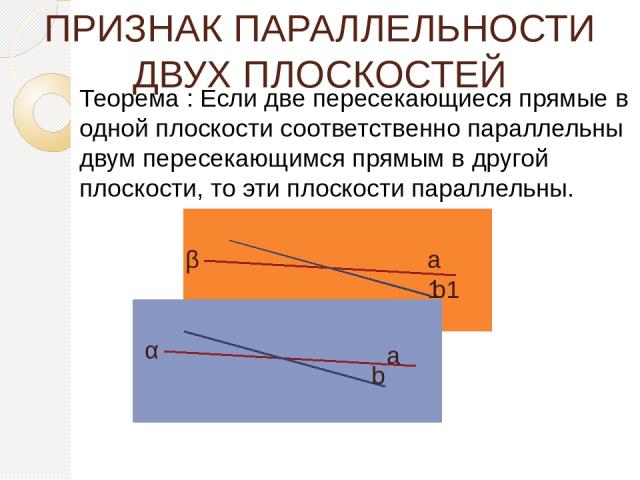
ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ДВУХ ПЛОСКОСТЕЙ Теорема : Если две пересекающиеся прямые в одной плоскости соответственно параллельны двум пересекающимся прямым в другой плоскости, то эти плоскости параллельны. α β а b а1 b1

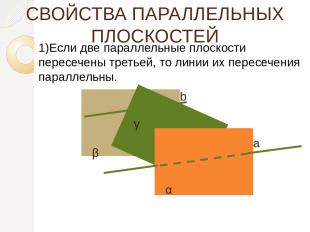
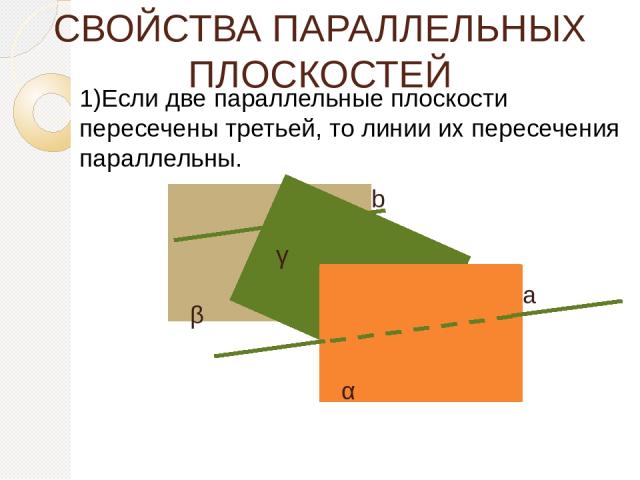
СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПЛОСКОСТЕЙ 1)Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. α β а b γ

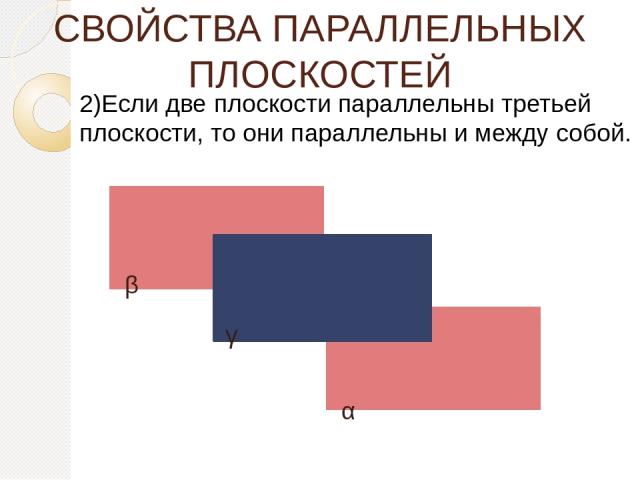
СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПЛОСКОСТЕЙ 2)Если две плоскости параллельны третьей плоскости, то они параллельны и между собой. α β γ

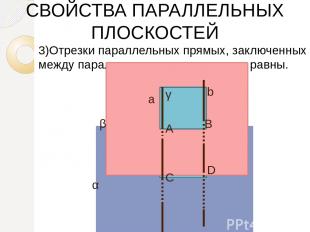
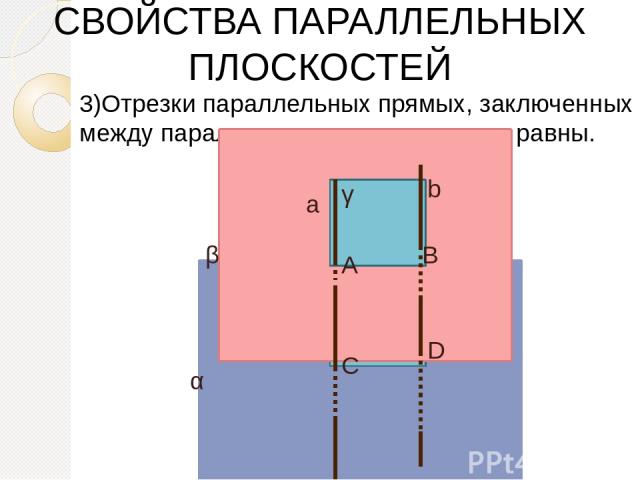
3)Отрезки параллельных прямых, заключенных между параллельными плоскостями, равны. СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПЛОСКОСТЕЙ α γ β а b А В С D